1.
Gradien dari persamaan 5x+3y=9 adalah ....
Pembahasan:
5x + 3y = 9
⇔ 3y = −5x + 9
⇔ y = −35x + 3
Persamaan garis lurus tersebut sudah memenuhi bentuk y = mx + c, maka gradiennya adalah −35.
2.
Perhatikan gambar berikut ini.
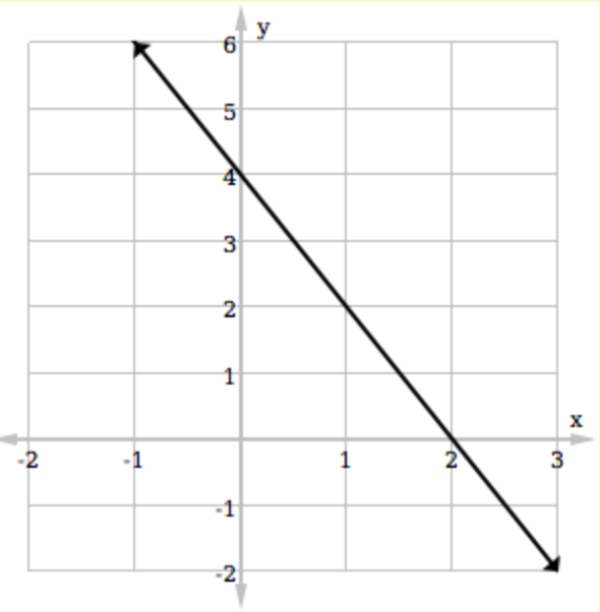
Gradien dari persamaan garis lurus yang ditunjukkan pada gambar di atas adalah ....
Pembahasan:
Perhatikan bahwa titik potong sumbu-x dan sumbu-y garis tersebut adalah (2,0) dan (0,4).
Untuk menentukan gradien suatu garis lurus jika diketahui (x1,y1) dan (x2,y2), bisa digunakan rumus
m = x2−x1y2−y1
Jadi, gradien garis lurus jika diketahui (2,0) dan (0,4) adalah
m = 0−24−0 =−24 = −2
Jadi, gradiennya adalah −2.
3.
Perhatikan grafik berikut.
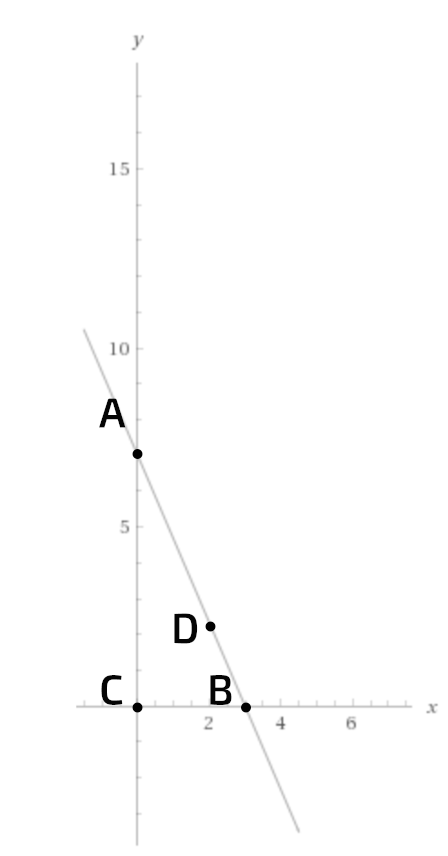
Penyelesaian persamaan garis lurus tersebut yang berpotongan dengan sumbu-x adalah titik ....
Pembahasan:
Titik A berpotongan dengan sumbu y; titik B berpotongan dengan sumbu-x; titik C bukan penyelesaian persamaan garis lurus tersebut; titik D merupakan salah satu penyelesaian persamaan garis lurus tersebut yang tidak berpotongan dengan sumbu-x atau pun sumbu-y. Jadi, jawaban yang tepat adalah titik B.
4.
Diketahui y=2x+2, maka untuk x=1, kita peroleh y=....
Pembahasan:
Diketahui persamaan y=2x+2, maka substitusikan nilai x=1
y=2x+2
=2(1)+2
=2+2
=4
5.
Grafik garis dengan persamaan 3x−2y=12 adalah ....
Pembahasan:
Dicari titik potong sumbu-x dan sumbu-y dari persamaan tersebut.
Titik potong dengan sumbu-x artinya y = 0.
Substitusi y = 0:
3x − 2(0) =12
⇔ 3x = 12
⇔ x =4
diperoleh titik potong sumbu-x (4,0).
Titik potong dengan sumbu-y artinya x = 0.
Substitusi x = 0:
3(0) − 2y = 12
⇔ 2y = 12
⇔ y = −6
diperoleh titik potong sumbu-y (0,−6).
Jadi, gambar grafik yang tepat adalah gambar yang garisnya melalui titik (4,0) dan (0,−6).
6.
Gradien dari garis lurus yang melewati titik (−2,1) dan (1,4) adalah ....
Pembahasan:
Diketahui:
Titik 1 (−2,1) dengan x1=−2 dan y1=1
Titik 2 (1,4) dengan x2=1 dan y2=4
Ditanya:
Gradien =m?
Dijawab:
Gradien dari persamaan garis lurus yang dilalui oleh titik (x1,y1) dan (x2,y2) dilambangkan oleh m dapat ditemukan dengan menggunakan rumus:
m=x2−x1y2−y1
Sehingga kita dapatkan:
m=x2−x1y2−y1
=1−(−2)4−1
=1+23
=33
=1
Jadi, dapat disimpulkan bahwa gradien dari persamaan garis yang dilalui oleh kedua titik tersebut adalah 1.
7.
Gradien garis yang melalui titik (2,1) dan (4,7) adalah ....
(UN Matematika SMP 2005)
Pembahasan:
Rumus persamaan garis yang melalui dua titik (x1,y1) dan (x2,y2) adalah
y2−y1y−y1=x2−x1x−x1
Jadi, persamaan garis yang melalui titik (2,1) dan (4,7) adalah
7−1y−1 =4−2x−2
⇔ 6y−1 =2x−2
⇔ 2(y − 1) = 6(x − 2)
⇔ 2y − 2 = 6x − 12
⇔ 2y = 6x − 12 + 2
⇔ 2y = 6x − 10
⇔ 22y = 26x − 210
⇔ y = 3x − 5
Persamaan garis lurus tersebut sudah memenuhi bentuk y = mx + c, maka gradiennya (m) adalah 3.
8.
Diantara persamaan garis berikut
(I). 2y=8x+20
(II). 6y=12x+18
(III). 3y=12x+15
(IV). 3y=−6x+15
yang grafiknya saling sejajar adalah ....
(UN Matematika SMP 2009)
Pembahasan:
(I). y = 4x + 10 → m = 4
(II). y = 2x + 3 → m = 2
(III). y = 4x + 5 → m = 4
(IV). y = −2x + 5 → m = −2
Dua persamaan saling sejajar apabila keduanya mempunyai gradien yang sama. Dengan demikian, diperoleh (I) dan (III) saling sejajar.
9.
Diketahui tiga titik di suatu sumbu koordinat membentuk segitiga siku-siku sama kaki ABC dengan sudut antara AB dan AC membentuk sudut siku-siku. Dua titik di antaranya adalah B(1,3) dan C(3,1). Persamaan garis lurus yang melalui titik A dengan gradien m=3 adalah ....
Pembahasan:
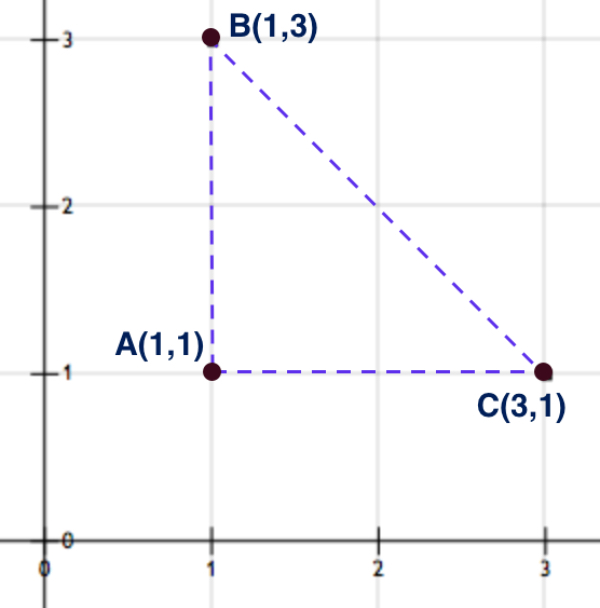
Dibuat gambar koordinat titik B(1,3) dan C(3,1). Dari yang diketahui ABC berbentuk segitiga siku-siku sama kaki dengan sudut antara AB dan AC membentuk sudut siku-siku, maka diperoleh titik A(1,1).
Rumus persamaan garis lurus yang melalui titik (x1,y1) dengan gradien m adalah y - y1 = m(x − x1).
Jadi, persamaan garis lurus yang melalui (1,1) dengan gradien m = 3 adalah
y − 1 = 3(x − 1)
⇔ y − 1 = 3x − 3
⇔ y = 3x − 3 + 1
⇔ y = 3x − 2
Jadi, persamaan garis lurus yang melalui titik A dengan gradien m = 3 adalah y = 3x − 2.
10.
Diketahui harga 2 kg apel dan 3 kg jerul Rp94.000,00 sedangkan harga 3 kg apel dan 2 kg jeruk Rp101.000,00. Harga 1 kg apel adalah ....
Pembahasan:
Misalkan
x = harga apel per kg
y = harga jeruk per kg
Ditanya: x = ...
Model matematika:
2x + 3y = 94.000 ... (i)
3x + 2y = 101.000 ... (ii)
Eliminasi (i) dan (ii)
2x + 3y = 94.000 |.2
3x + 2y = 101.000 |.3
4x + 6y = 188.000
9x + 6y = 303.000 −
−5x = −115.000 ⇔ x = 23.000
Jadi, harga 1 kg apel adalah Rp23.000,00.
