1.
Manakah diantara pola noktah-noktah berikut yang menunjukkan pola bilangan ganjil?
Pembahasan:
Gambar 1 :

Noktah di atas menunjukkan pola bilangan persegipanjang.
Gambar 2 :

Noktah di atas menunjukkan pola bilangan segitiga.
Gambar 3 :

Noktah di atas menunjukkan pola bilangan ganjil (1, 3, 5, 7).
Gambar 4 :

Noktah di atas menunjukkan pola bilangan persegipanjang.
3.
Pola bilangan segitiga pascal pada baris ke-6 adalah ....
Pembahasan:
Berikut adalah pola yang terbentuk pada segitiga pascal:
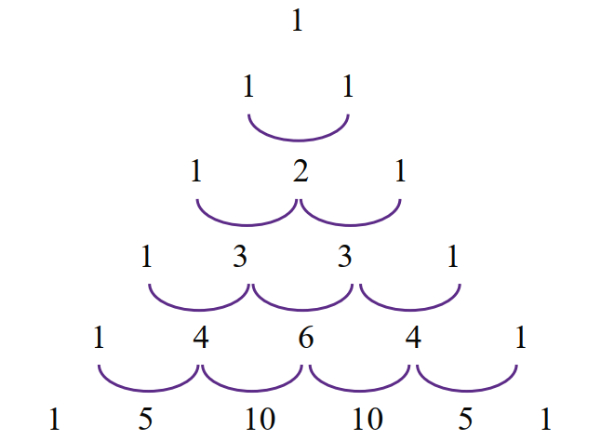
Baris pertama segitiga pascal dihitun dari puncak. Maka pola yang akan terbentuk pada baris ke-6 adalah 1 - 5 - 10 - 10 - 5 - 1
4.
Di antara berbagai macam pola bilangan, Pola Penambahan Tetap dapat menghasilkan berbagai macam barisan bilangan, salah satunya bilangan asli yang ditujukan pada pilihan ....
Pembahasan:
Barisan bilangan yang diperoleh dari Pola Penambahan Tetap dapat diperoleh dari penambahan yang tetap dari suku sebelumnya.
Untuk bilangan asli, dilakukan penambahan satu-satu (+1 ), sehingga pilihan yang tepat adalah 1, 2, 3, 4, 5, ...
*Barisan 1, 3, 4, 7, 11, ...
Barisan tersebut merupakan barisan Fibonacci yang bukan diperoleh dari pola penambahan tetap
*Barisan 2, 3, 5, 8, 12, ...
Barisan tersebut diperoleh dari penambahan bilangan yang tidak tetap, yaitu bilangan asli secara berurutan yang dimulai dari angka 1.
*Barisan 3, 4, 4, 6, 12, 15, ...
Barisan tersebut tidak diperoleh dari penambahan bilangan tetap, tetapi penjumlahan (penambahan) dan perkalian secara bergantian dengan bilangan asli yang dimulai dari angka 1.
5.
Jika m,(2m+3),(4m+9) adalah 3 suku berurutan barisan geometri, maka berapa rasio antarsukunya?
Pembahasan:
Rasio antar suku dalam barisan geometri dicari dengan:
r=Un−1Un
Dari barisan geometri di soal, dapat diketahui
U1=m , U2=2m+3 , U3=4m+9
1) Sebelum menghitung rasio, kita perlu mengetahui nilai m. Nilai m dapat diperoleh dengan membuat persamaan rasio barisan geometri.
r = U1U2=U2U3
m2m+3 = 2m + 34m + 9
(2m+3)(2m+3)=m(4m+9)
4m2+6m+6m+9=4m2+9m
4m2−4m2+6m+6m−9m=−9
3m=−9
m=−3
2) Substitusi nilai m ke suku-suku yang diketahui
U1=m=−3
U2=2m+3=2.−3+3=−3
U3=4m+9=4.−3+9=−3
3) Cari rasio
r=U1U2=−3−3=1
6.
Suatu barisan bilangan mempunyai rumus suku ke-n, yaitu Un=6n−5.
Suku ke- berapakah yang mempunyai nilai 103?
Pembahasan:
Diketahui:
Un=6n−5
Suatu suku mempunyai nilai 103, maka Un=103. Substitusi nilai Un=103 ke Un=6n−5.
103=6n−5
103+5=6n
108=6n
n=18
7.
Sebuah barisan Fibonacci memiliki U2 = 9 dan U8 = 157. Berapakah suku awal barisan Fibonacci tersebut?
Pembahasan:
Barisan bilangan Fibonacci adalah barisan bilangan yang diperoleh dari penjumlahan 2 suku sebelumnya.
Bentuk umum untuk barisan bilangan Fibonacci adalah
a, b, (a+b), (b+[a+b]), ...
Pada barisan ini diketahui suku ke-2 atau U2 = 9 dan suku ke-8 U8 = 157. Pada dasarnya barisan Fibonacci hanya berawal dari 2 angka/suku yang dijumlahkan secara terus menerus.
Coba perhatikan tabel di bawah ini!

Berdasarkan tabel di atas, dapat dihitung bahwa :
U8 = U6 + U7
= (3a + 5b) + (5a + 8b)
= 8a + 13b
Diketahui b = U2 = 9, maka :
U8 = 8a + (13×9)
157 = 8a + 117
8a = 157 - 117
a =840
a = 5
Jadi, suku awal barisan Fibonacci tersebut adalah 5.
8.
Berapa jumlah satuan persegi yang berwarna merah pada pola ke-61?
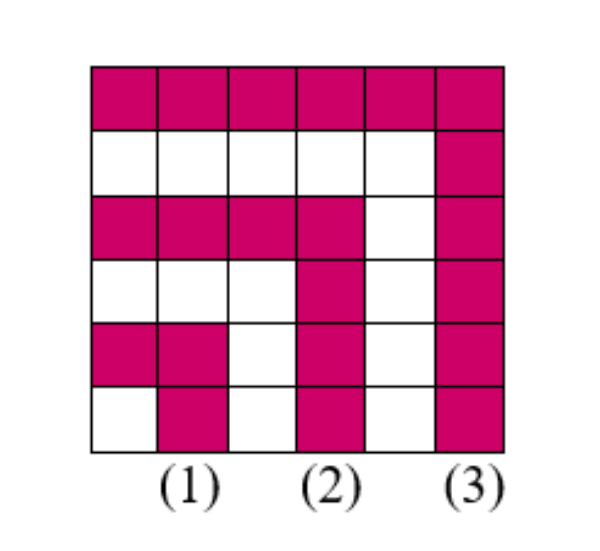
Pembahasan:
Perhatikan pola persegi berwarna merah. Barisan bilangan yang terbentuk:
3, 7, 11, ...
Setelah memperhatikan pola persegi warna merah pada gambar, diketahui terdapat penambahan 4 satuan persegi pada setiap pola yang baru. Sehingga dapat diketahui bahwa gambar membentuk barisan Aritmatika.
Maka,
Suku pertama = a = 3
Selisih antar suku / beda = b = 7 - 3 = 4
Rumus menentukan suku ke-n pada barisan Aritmetika adalah,
Un = a + (n−1)b
Jadi, jumlah persegi warna merah pada pola/suku ke-61 adalah
U61 = 3 + (61 - 1) 4
U61 = 3 + 240
U61 = 243 satuan persegi
9.
Jika Sn=2n2+3n adalah rumus jumlah n suku pertama deret aritmetika, maka berapakah nilai U9?
Pembahasan:
Langkah pertama adalah mencari nilai n dari rumus Sn yang tersedia. Perlu diingat bahwa a=S1 karena jumlah 1 suku sama dengan suku awal barisan/deret tersebut. Oleh karena itu, kita masukkan n=1 ke Sn=2n2+3n .
S1=2(1)2+3(1)
S1=2+3
S1=a=5
Langkah kedua, cari beda deret tersebut
Untuk mengetahui beda deret tersebut, cari S2
S2=2(2)2+3(2)
S2=2(4)+3(2)
S2=8+6
S2=14 → artinya jumlah 2 suku pertama adalah 14
Maka, suku ke-2 (U2) bisa kita cari dengan cara S2−a = 14 - 5 = 9
b=U2−U1=9−5=4
Langkah terakhir, cari nilai U9
Un=a+(n−1)b
U9=5+(9−1)4
U9=5+8.4
U9=5+32
U9=37
10.
Sebuah barisan dengan tiga suku pertama secara berurutan adalah : (m+2), 2m, 31 merupakan barisan aritmetika, berapakah beda antar suku berurutan pada barisan tersebut?
Pembahasan:
Rumus umum barisan Aritmetika :
Un = a+(n−1)b
Dimana,
a = Suku pertama barisan
b = Beda selisih antar suku berurutan
n = Urutan bilangan (Suku ke-)
Diketahui :
U1 = m + 2
U2 = 2m
U3 = 31
b = U2 - U1
= 2m - (m + 2)
= 2m - m - 2
= m - 2
Untuk mencari nilai suku ke-2, perlu mengetahui besar nilai m.
U3 = U2 + b
31 = 2m + (m - 2)
31 = 3m - 2
3m = 33
m = 11
Maka, beda antar suku dapat dihitung dengan cara substitusi nilai y ke dalam persamaan b
b = m - 2
= 11 - 2
= 9
