1.
Diketahui dua garis sejajar yang dipotong oleh sebuah garis lain. Pasangan sudut yang memiliki jumlah 180o adalah ....
Pembahasan:
Agar lebih jelas, perhatikan gambar berikut!
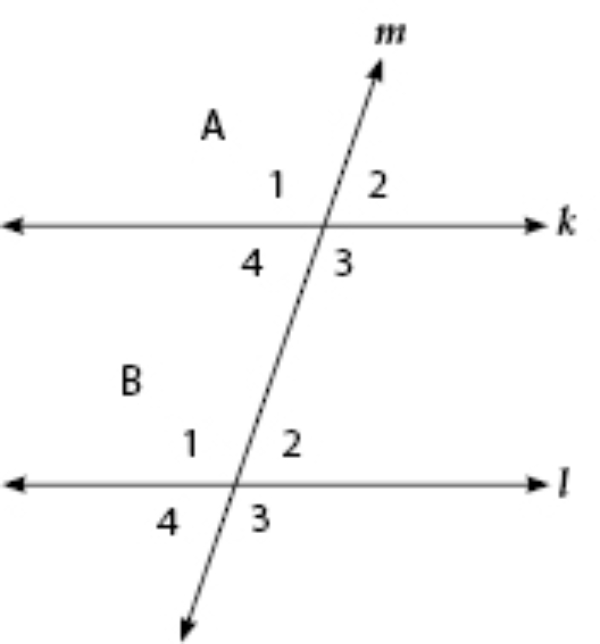
Pada gambar terlihat garis sejajar k dan l, serta garis m yang memotong garis k dan l.
Sudut-sudut yang merupakan pasangan sudut sehadap adalah ∠A1 dan ∠B1, ∠A2 dan ∠B2, ∠A3 dan ∠B3, serta ∠A4 dan ∠B4. Pada gambar dapat dilihat bahwa besar sudut pasangan sudut sehadap adalah sama.
Sudut-sudut yang merupakan pasangan sudut dalam berseberangan adalah ∠A4 dan ∠B2 serta ∠A3 dan ∠B1. Pada gambar dapat dilihat bahwa besar sudut pasangan sudut dalam berseberangan adalah sama.
Sudut-sudut yang merupakan pasangan sudut luar berseberangan adalah ∠A1 dan ∠B3 serta ∠A2 dan ∠B4. Pada gambar dapat dilihat bahwa besar sudut pasangan sudut luar berseberangan adalah sama.
Sudut-sudut yang merupakan pasangan sudut dalam sepihak adalah ∠A4 dan ∠B1 serta ∠A3 dan ∠B2. Pada gambar dapat dilihat bahwa besar sudut pasangan sudut dalam sepihak tidak sama, atau jika dijumlahkan hasilnya adalah 180o.
2.
Ukuran keempat sudut yang dimiliki oleh persegi adalah ....
Pembahasan:
Bentuk persegi seperti gambar di bawah ini.

Keempat sudut persegi adalah siku-siku yang besarnya 90o.
Jadi, ukuran keempat sudut yang dimiliki oleh persegi adalah 90o.
3.
Ruas garis AH dibagi menjadi 9 bagian sama panjang seperti gambar berikut.

Perbandingan antara panjang NU dan LQ adalah ....
Pembahasan:
Untuk lebih jelasnya, perhatikan gambar berikut!
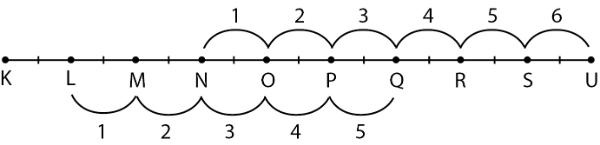
Pada gambar terlihat panjang NU adalah 6 ruas garis, sedangkan panjang LQ adalah 5 ruas garis. Jadi, perbandingan antara panjang NU dan LQ adalah 6 : 5.
4.
Hubungan dua sudut yang jika dijumlahkan hasilnya adalah 180o disebut ....
Pembahasan:
Hubungan dua sudut disebut sudut berpelurus jika jumlah kedua sudut adalah 180o.
*Hubungan dua sudut disebut sudut berpenyiku jika jumlah kedua sudut adalah 90o.
*Sudut berkomplemen adalah nama lain dari sudut berpenyiku, jadi hubungan dua sudut berkomplemen jika jumlah kedua sudut adalah 90o.
*Sudut bertolak belakang adalah dua sudut yang saling bertolak belakang. Sudut yang bertolak belakang besarnya sama.
5.
Perhatikan gambar berikut!
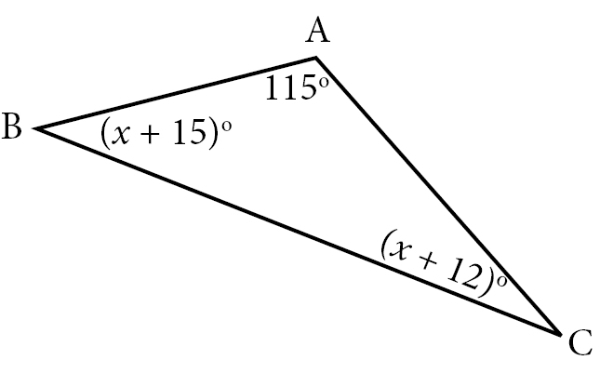
Besar sudut ABC adalah ....
Pembahasan:
Jumlah sudut pada sebuah segitiga adalah 180o. Sehingga, ketiga sudut pada segitiga ABC jika dijumlahkan hasilnya adalah 180o.
∠ABC + ∠BCA + ∠CAB = 180o
(x + 15)o + (x + 12)o + 115o = 180o
2xo + 27o + 115o = 180o
2xo + 142o = 180o
2xo = 180o − 142o
2xo = 38o → x = 238 = 19
Ditanyakan besar sudut ABC.
∠ABC = (x + 15)o = (19 + 15)o = 34o
6.
Diketahui sudut U dan sudut V adalah dua sudut yang saling berpelurus. Jika besar sudut U sama dengan 119 bagian dari sudut pelurusnya, maka besar sudut V adalah ....
Pembahasan:
Diketahui sudut U dan sudut V adalah dua sudut yang saling berpelurus, maka ∠U + ∠V = 180o.
Pelurus ∠U adalah ∠V, sehingga ∠U = 119 ∠V.
Maka
∠U + ∠V = 180o
119 ∠V + ∠V = 180o (Kalikan semua dengan 11)
9∠V + 11∠V = 1980o
20∠V = 1980o → ∠V = 201980o = 99o
7.
Perhatikan gambar berikut!
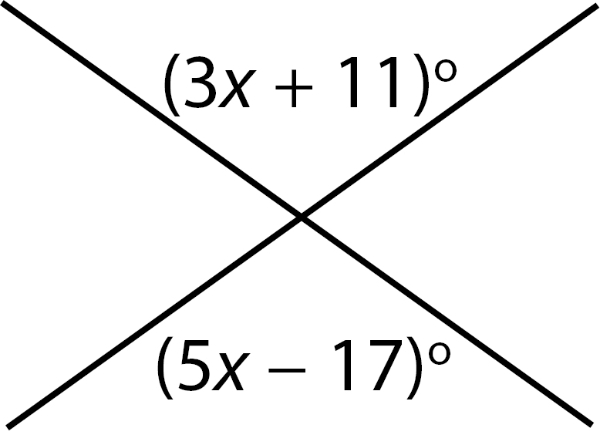
Nilai x yang memenuhi gambar di atas adalah ....
Pembahasan:
Pada gambar terlihat sudut yang besarnya (3x + 11)o dan sudut yang besarnya (5x − 17)o merupakan dua sudut yang saling bertolak belakang. Sudut yang saling bertolak belakang besarnya sama. Maka
(3x + 11)o = (5x − 17)o
11o + 17o = 5xo − 3xo
28o = 2xo → x = 228 = 14
8.
Diketahui ruas garis DF dengan panjang 56 cm. Titik E terletak di antara titik D dan F sehingga DE : EF = 3 : 5. Panjang DE adalah ....
Pembahasan:
Berdasarkan soal, didapatkan gambar sebagai berikut.
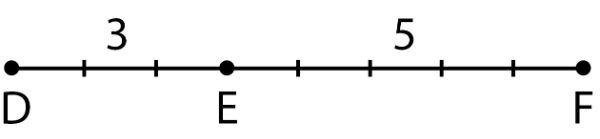
Diketahui panjang DF = 56 cm dan perbandingan DE : EF = 3 : 5. DF terdiri dari DE dan EF, sehingga nilai perbandingan DF adalah 3 + 5 = 8.
Maka panjang DE adalah
DE = 83 × 56 cm = 3 × 7 cm = 21 cm
9.
Perhatikan gambar berikut!
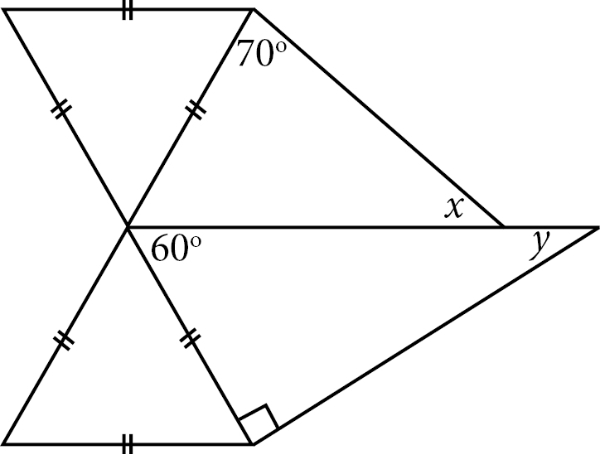
Nilai dari yx adalah ....
Pembahasan:
Pada gambar terdapat dua segitiga sama sisi. Segitiga sama sisi memiliki tiga sudut yang sama besar, yaitu 60o. Sehingga didapatkan besar sudut sebagai berikut.
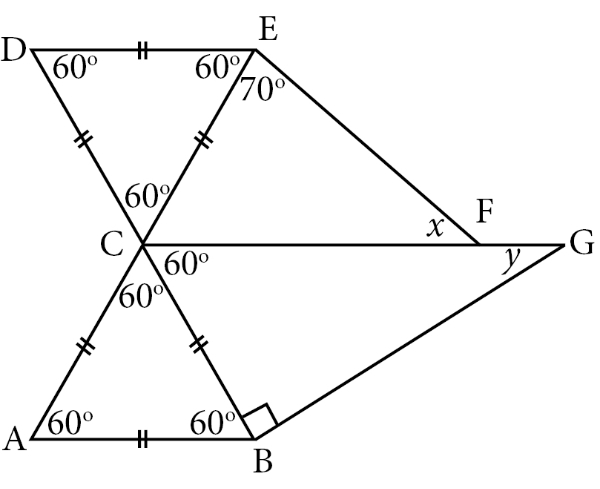
Mencari nilai x
Pada gambar terlihat garis AE terbagi menjadi 3 sudut, yaitu ∠ACB, ∠BCG, dan ∠ECF. Sebuah garis lurus sudutnya 180o, sehingga ketiga sudut yang membagi AE jika dijumlahkan hasilnya adalah 180o.
∠ACB + ∠BCG + ∠ECF = 180o
60o + 60o + ∠ECF = 180o
120o + ∠ECF = 180o
∠ECF = 180o − 120o = 60o
Sebuah segitiga memiliki jumlah sudut 180o. Sehingga sudut pada segitiga CEF jika dijumlahkan hasilnya adalah 180o.
∠ECF + ∠CFE + ∠FEC = 180o
60o + x + 70o = 180o
130o + x = 180o
x = 180o − 130o = 50o
Mencari nilai y
Sebuah segitiga memiliki jumlah sudut 180o. Sehingga sudut pada segitiga BCG jika dijumlahkan hasilnya adalah 180o.
∠CBG + ∠BGC + ∠BCG = 180o
90o + y + 60o = 180o
150o + y = 180o
y = 180o − 150o = 30o
Ditanyakan nilai dari
yx = 30o50o = 35
10.
Perhatikan gambar berikut!
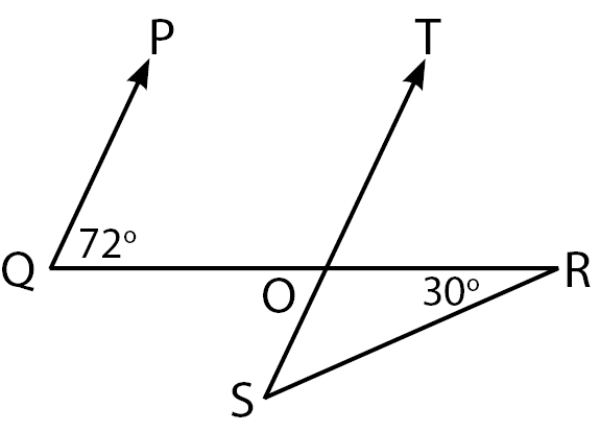
Besar ∠RSO yang memenuhi gambar di atas adalah ....
Pembahasan:
Mencari besar ∠TOR
Pada gambar terlihat ∠PQO dan ∠TOR menghadap ke arah yang sama terhadap dua garis sejajar, sehingga ∠PQO dan ∠TOR merupakan pasangan sudut sehadap. Pasangan sudut sehadap besarnya sama, maka besar ∠PQO = ∠TOR = 72o.
Mencari besar ∠ROS
Garis lurus ST terlihat terbagi menjadi dua sudut, yaitu ∠TOR dan ∠ROS. Karena membagi garis lurus, maka ∠TOR dan ∠ROS merupakan pasangan sudut yang saling berpelurus. Sudut yang saling berpelurus jika dijumlahkan hasilnya 180o.
∠TOR + ∠ROS = 180o (Substitusi besar ∠TOR yang telah didapat)
72o + ∠ROS = 180o → ∠ROS = 180o − 72o = 108o
Mencari besar ∠RSO
Pada gambar terbentuk segitiga RSO. Segitiga RSO memiliki 3 sudut, yaitu ∠ROS, ∠ORS, dan ∠RSO. Jumlah ketiga sudut pada segitiga adalah 180o, maka jumlah ∠ROS, ∠ORS, dan ∠RSO adalah 180o.
∠ROS + ∠ORS + ∠RSO = 180o
108o + 30o + ∠RSO = 180o
138o + ∠RSO = 180o
∠RSO = 180o − 138o = 42o
