Bank Soal Matematika SMA Operasi Invers Komposisi Fungsi
Soal
KurMer Kelas XI Matematika Komposisi Fungsi dan Fungsi Invers Skor 3
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Dalam tata tertib penggunaan laboratorium, para praktikan diwajibkan menggunakan baju khusus praktikum. Baju ini memiliki standar tertentu, yaitu berlengan panjang, panjang baju sampai di bawah lutut, dan berwarna putih. Tujuan penggunaan jas laboratorium adalah ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Bekerja di Laboratorium
Choose the correct answer.
Mr. Eddie ... (not/watch) a football match right now.
Bahasa Inggris
Level 10
Congratulating and Complimenting
Tenses: Simple Present & Present Continuous

Sumber: https://www.freepik.com/
Pada sebuah kegiatan eksperimen, seorang siswa mencampurkan metanol yang dia ambil dari kemasan berlabel seperti pada gambar. Bahan tersebut akan digunakan sebagai antibeku di dalam eksperimennya. Tetapi, pada saat mengambil bahan tersebut dia menghirupnya karena penasaran dan tiba-tiba mengalami penurunan kesadaran. Salah satu langkah yang tepat sebagai upaya pertolongan pertama pada kecelakaan tersebut adalah ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Keselamatan Kerja di Laboratorium
Berikut ini pernyataan yang tepat tentang agroekosistem adalah ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tingkat Keanekaragaman Hayati
EDIT: jawaban seharusnya adalah HP
Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Pertidaksamaan Linear Satu Variabel dengan Nilai Mutlak
Film Dilan: 1990 menjadi salah satu film Indonesia dengan jumlah penonton terbanyak.
Penulisan judul film yang benar adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Menulis Teks Laporan Hasil Observasi
Pada jaring-jaring makanan di bawah ini, organisme X berperan sebagai ....
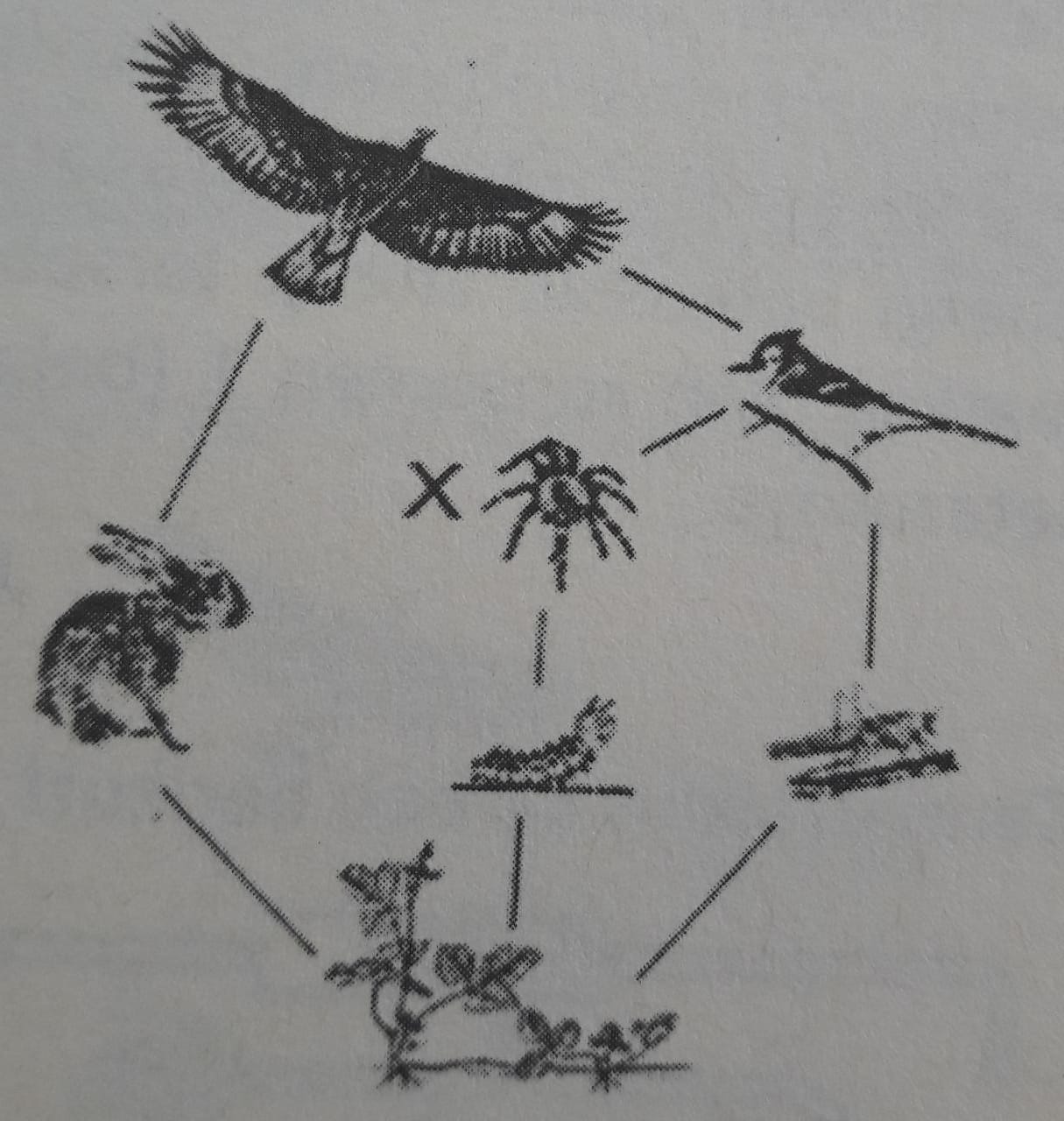
(UN 2014)
Biologi
Level 10
Biologi
Ekologi
Aliran Energi dan Piramida Ekologi
Salah satu manfaat virus adalah untuk pembuatan vaksin. Vaksin dapat dibuat melalui metode konvensional dan modern (rekayasa genetika). Di bawah ini yang termasuk ke dalam vaksin dengan metode konvensional dari patogen yang dilemahkan adalah ….
Biologi
Level 10
Biologi
Virus
Pencegahan dan Pengobatan Infeksi Virus
Perhatikan alat-alat laboratorium berikut ini!
- Labu ukur
- Kaki tiga
- Gelas arloji
- Penjepit tabung
- Lampu spiritus
Pada saat kelas praktikum kimia, Intan ingin memanaskan larutan yang ada di dalam gelas kimia. Peralatan yang dibutuhkan untuk melakukan aktivitas tersebut adalah ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Metode Ilmiah dan Laboratorium Kimia
Daerah arsiran pada gambar berikut merupakan hasil penyelesaian dari sistem pertidaksamaan ....
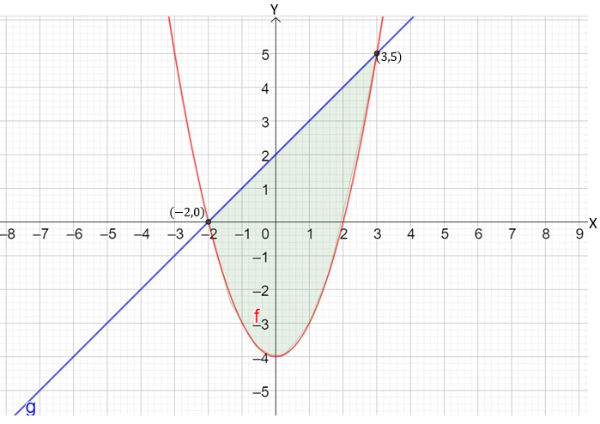
Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Sistem Pertidaksamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Dalam tata tertib penggunaan laboratorium, para praktikan diwajibkan menggunakan baju khusus praktikum. Baju ini memiliki standar tertentu, yaitu berlengan panjang, panjang baju sampai di bawah lutut, dan berwarna putih. Tujuan penggunaan jas laboratorium adalah ....
Choose the correct answer.
Mr. Eddie ... (not/watch) a football match right now.
Sumber: https://www.freepik.com/
Pada sebuah kegiatan eksperimen, seorang siswa mencampurkan metanol yang dia ambil dari kemasan berlabel seperti pada gambar. Bahan tersebut akan digunakan sebagai antibeku di dalam eksperimennya. Tetapi, pada saat mengambil bahan tersebut dia menghirupnya karena penasaran dan tiba-tiba mengalami penurunan kesadaran. Salah satu langkah yang tepat sebagai upaya pertolongan pertama pada kecelakaan tersebut adalah ....
Berikut ini pernyataan yang tepat tentang agroekosistem adalah ....
EDIT: jawaban seharusnya adalah HP
Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah ....
Film Dilan: 1990 menjadi salah satu film Indonesia dengan jumlah penonton terbanyak.
Penulisan judul film yang benar adalah ….
Pada jaring-jaring makanan di bawah ini, organisme X berperan sebagai ....

(UN 2014)
Salah satu manfaat virus adalah untuk pembuatan vaksin. Vaksin dapat dibuat melalui metode konvensional dan modern (rekayasa genetika). Di bawah ini yang termasuk ke dalam vaksin dengan metode konvensional dari patogen yang dilemahkan adalah ….
Perhatikan alat-alat laboratorium berikut ini!
- Labu ukur
- Kaki tiga
- Gelas arloji
- Penjepit tabung
- Lampu spiritus
Pada saat kelas praktikum kimia, Intan ingin memanaskan larutan yang ada di dalam gelas kimia. Peralatan yang dibutuhkan untuk melakukan aktivitas tersebut adalah ....
Daerah arsiran pada gambar berikut merupakan hasil penyelesaian dari sistem pertidaksamaan ....



