Pembahasan:

Diketahui:

f(x)=3(x2−4x+10) . 

Ditanya:

Nilai pernyataan?

Dijawab:

• Pernyataan: Fungsi  f bersifat definit positif.

Fungsi kuadrat  f(x)=ax2+bx+c bersifat definit positif jika nilai  a>0 dan nilai diskriminan kurang dari  0 ( D<0 ).

Dari fungsi:

f(x)=3(x2−4x+10)

⇔f(x)=3x2−12x+30   

Diketahui nilai a=3,b=−12 dan  c=30 .

Selanjutnya, kita cari nilai diskriminan.   

D=b2−4ac  

⇔D=(−12)2−(4×3×30)   

⇔D=144−360  

⇔D=−216 (Nilai diskriminan kurang dari 0)

Pernyataan bernilai benar.

• Pernyataan: Grafik fungsi  f  memotong garis   y=20 .   

Untuk membuktikan apakah grafik fungsi  f  memotong garis   y=20 , kita substitusikan persamaan garis ke persamaan grafik. Selanjutnya, mencari nilai diskriminannya. Grafik fungsi  f  memotong garis   y=20 jika nilai diskriminannya lebih dari 0  (D>0) .

  f(x)=y  

  ⇔3(x2−4x+10)=20   

Bagi kedua ruas dengan 3.

x2−4x+10=320​   

⇔x2−4x+330​−320​=0   

⇔x2−4x+310​=0   

 Mencari nilai diskriminan.

D=b2−4ac  

⇔D=(−4)2−(4×1×310​)  

⇔D=16−340​  

⇔D=348​−340​  

⇔D=38​

Diskriminan > 0 → ada 2 titik potong nyata, berarti grafik parabola memotong garis y = 20.

Pernyataan bernilai benar.

• Pernyataan: Titik puncak grafik  f berada di sebelah kiri sumbu-Y.

Posisi titik puncak dapat diketahui berdasarkan absisnya. Rumus untuk mencari absis:

  xp​=2a−b​   

Dari perhitungan, sebelumnya diketahui nilai a=3,b=−12 dan  c=30 .

Sehingga:

  xp​=2a−b​  

=2×3−(−12)​   

=2   (Karena  xp​=2 , berarti titik puncak berada di sebelah kanan sumbu-Y.)

Pernyataan bernilai salah.

Jadi, nilai pernyataan

• Fungsi  f bersifat definit positif. (Benar)

• Grafik fungsi  f  memotong garis   y=20 . (Benar)

• Titik puncak grafik  f berada di sebelah kiri sumbu-Y. (Salah)

Pembahasan:

Diketahui:

Diberikan kubus ABCD.EFGH dengan panjang rusuk 6 cm.

Ditanya:

Nilai kebenaran pernyataan?

Dijawab:

Perhatikan kubus ABCD.EFGH berikut dengan panjang rusuk 6 cm.

• Pernyataan: Panjang diagonal ruang BH  adalah  6√3 cm.

Pada kubus dengan panjang rusuk  s , panjang diagonal ruang adalah  s√3 . 

Pada kubus ABCD.EFGH di atas, panjang diagonal ruang BH adalah  6√3 cm.

Pernyataan bernilai benar.

• Pernyataan: Jarak titik  A  ke garis CH adalah 2√6  cm.

Pada kubus ABCD.EFGH, jarak A ke CH merupakan tinggi dari segitiga sama sisi ACH. 

  AC=AH=CH=√62+62​=6√2 cm

Tinggi segitiga sama sisi dengan panjang sisi  a dapat dicari menggunakan rumus 21​×a×√3 . 

Sehingga, tinggi segitiga  ACH :

t=21​×a×√3     

=21​×(6√2)×(√3)   

=3√6 cm

Pernyataan bernilai salah.

•  Pernyataan: Jarak titik B ke bidang ADHE adalah 6 cm.

Jarak titik B ke ADHE adalah AB. Panjang AB adalah 6 cm.

Pernyataan bernilai benar.

Jadi:

• Panjang diagonal ruang BH  adalah  6√3 cm. (Benar)
• Jarak titik A  ke garis CH adalah 2√6  cm. (Salah)
• Jarak titik B ke bidang ADHE adalah 6 cm. (Benar)

Pembahasan:

Diketahui:

• Waktu generasi = waktu untuk membentuk bakteri menjadi dua kalinya, berarti $r=2$
• Waktu generasi = 17 menit
• Pemilihan suatu metode bergantung pada jumlah bakteri hasil pembiakan terbanyak yang bisa dihasilkan selama waktu pembelahan
• Waktu pembelahan = 51 menit

Ditanya:

Jumlah bakteri dari dua metode yang dapat dipilih?

Dijawab:

Jumlah bakteri setelah membelah sebanyak $n$ kali dapat dihitung menggunakan rumus:

$U_n=ar^n$ , di mana $n=\frac{t}{tg}$

Keterangan:

$U_n$ = jumlah bakteri setelah membelah sebanyak $n$ kali

$a$ = jumlah bakteri mula-mula

$r$ = rasio

$n$ = jumlah pembelahan

$t$ = waktu pembelahan

$tg$ = waktu generasi

MENENTUKAN 2 METODE DENGAN JUMLAH BAKTERI HASIL PEMBIAKAN PALING BANYAK DALAM 51 MENIT:

Perhatikan tabel berikut!

Karena pembiakan hanya dibatasi hingga menit ke-51, berarti penambahan bakteri pada metode 2, 3, dan 4 belum dilakukan. Oleh karena itu, penentuan 2 metode yang menghasilkan bakteri paling banyak dapat dilakukan berdasarkan jumlah bakteri mula-mula. Berdasarkan tabel, 2 metode dengan jumlah bakteri mula-mula terbanyak adalah metode 1 (20) dan metode 2 (15).

JUMLAH PEMBELAHAN HINGGA MENIT KE-51:

$n=\frac{t}{tg}=\frac{51}{17}=3$

JUMLAH BAKTERI PADA MENIT KE-51 MENGGUNAKAN METODE 1:

Jumlah bakteri setelah membelah sebanyak $n=3$ kali:

$U_n=ar^n$

$=20\times2^3$

$=160$

JUMLAH BAKTERI PADA MENIT KE-51 MENGGUNAKAN METODE 2:

Jumlah bakteri setelah membelah sebanyak $n=3$ kali:

$U_n=ar^n$

$=15\times2^3$

$=120$

Jadi, dua metode yang dapat dipilih menghasilkan 120 unit CFU dan 160 unit CFU.

Pembahasan:

Diketahui:

• Modal yang tersedia adalah Rp3.000.000,00.
• Biaya produksi es sarang burung adalah Rp6.000,00 per porsi dan dijual dengan laba 40% dari biaya produksi.
• Biaya produksi es campur adalah Rp10.000,00 per porsi dan dijual dengan laba 30% dari biaya produksi.
• Pengusaha hanya mampu membuat 450 porsi pencuci mulut.

Ditanya:

Nilai kebenaran pernyataan?

Dijawab:

Mencari daerah penyelesaian:

Misalkan:

• Jumlah es sarang burung yang diproduksi =  x  
• Jumlah es campur yang diproduksi =  y  

Dari informasi pada soal, dapat dituliskan pertidaksamaan linear sebagai berikut.

• 6.000x+10.000y≤3.000.000 , pertidaksamaan ini dapat disederhanakan menjadi  3x+5y≤1.500  
•   x+y≤450  
•   x≥0,y≥0  

Pertidaksamaan dapat digambarkan sebagai berikut.

Mencari keuntungan maksimum:

Keuntungan per porsi es sarang burung = 40% × Rp6.000,00 = Rp2.400,00.

Keuntungan per porsi es campur = 30% × Rp10.000,00 = Rp3.000,00.

Fungsi tujuan dapat dituliskan sebagai 

  f(x,y)=2.400x+3.000y  

Keuntungan maksimum didapat dengan uji coba tiap titik pojok daerah penyelesaian. 

• Titik O adalah (0,0)
• Titik A

Titik A dapat dicari dengan substitusi  x=0 ke persamaan garis  3x+5y=1.500 .

  3(0)+5y=1.500  

⇔5y=1.500      

⇔y=300   

Sehingga, titik A (0,300).

• Titik B

Titik B dapat dicari dengan substitusi   y=0   ke persamaan garis   x+y=450 . 

0+y=450   

⇔y=450    

Sehingga, titik B(450,0)

• Titik C

Titik C adalah titik potong garis  x+y=450 dan  3x+5y=1.500 . 

Substitusi  y=450−x ke  3x+5y=1.500 . 

3x+5(450−x)=1.500  

⇔3x+2.250−5x=1.500   

⇔−2x=−750   

⇔x=375   

Substitusi  x=375 ke persamaan  x+y=450 . 

375+y=450  

⇔y=75    

Sehingga, titik C(375,75) 

Mencari nilai kebenaran dari masing-masing pernyataaan.

• Pernyataan: Es sarang burung harus diproduksi lebih banyak dari es campur untuk mendapatkan keuntungan maksimum.

Keuntungan maksimum tercapai dengan memproduksi 375 porsi es sarang burung dan 75 porsi es campur (es sarang burung diproduksi lebih banyak dari es campur). 

Pernyataan bernilai benar.

• Pernyataan: Keuntungan maksimum yang dapat diperoleh adalah Rp1.500.000,00.

Dari tabel uji coba titik pojok, diperoleh keuntungan maksimum adalah Rp1.125.000,00.

Pernyataan bernilai salah.

• Pernyataan: Modal yang tersedia dapat digunakan untuk memproduksi lebih dari 450 porsi pencuci mulut.

Biaya produksi terendah adalah membuat es sarang burung yaitu Rp6.000,00 per porsi.

Modal Rp3.000.000,00 dapat digunakan untuk memproduksi:

6.0003.000.000​ = 500 porsi es sarang burung.

Meskipun tidak mendapatkan keuntungan yang maksimal, adalah benar kalau modal yang tersedia dapat digunakan untuk memproduksi lebih dari 450 porsi pencuci mulut.

Pernyataan bernilai benar.

Jadi, 

• Es sarang burung harus diproduksi lebih banyak dari es campur untuk mendapatkan keuntungan maksimum. (Benar)
• Keuntungan maksimum yang dapat diperoleh adalah Rp1.500.000,00. (Salah)
• Modal yang tersedia dapat digunakan untuk memproduksi lebih dari 450 porsi pencuci mulut. (Benar)

Pembahasan:

Diketahui:

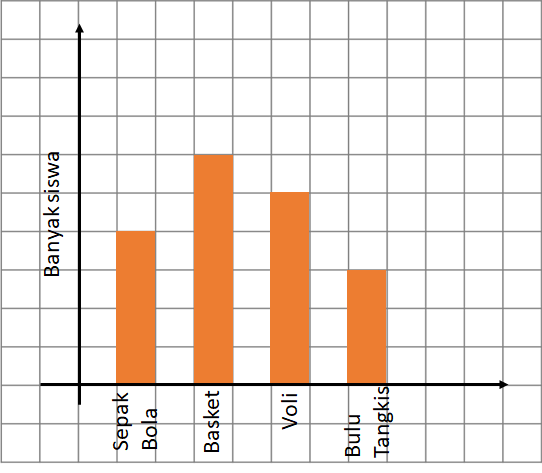
Banyak siswa yang menyukai sepak bola $=28$ siswa

Ditanya:

Persentase siswa yang menyukai olahraga basket?

Banyak siswa yang menyukai olahraga basket?

Jawab:

Perhatikan bahwa sepak bola dalam diagram batang di atas dinyatakan dalam 4 petak persegi sehingga dapat ditulis:

$4$ petak persegi $=28$ siswa, maka

$1$ petak persegi $=\frac{28}{4}$

$1$ petak persegi $=7$ siswa.

Hal ini berarti 1 petak persegi pada diagram batang di atas mewakili 7 siswa.

Untuk menghitung persentase siswa yang menyukai olahraga basket, kita perlu menemukan jumlah siswa yang didata terlebih dahulu.

Banyak siswa yang menyukai olahraga basket.

Perhatikan bahwa basket dalam diagram di atas dinyatakan dalam 6 petak persegi, sehingga banyak siswa yang menyukai basket dapat dinyatakan sebagai berikut.

Banyak siswa suka basket $=6\times7$

Banyak siswa suka basket $=42$ siswa.

Banyak siswa yang menyukai olahraga voli

Perhatikan bahwa voli dalam diagram di atas dinyatakan dalam 5 petak persegi, sehingga banyak siswa yang menyukai voli dapat dinyatakan sebagai berikut.

Banyak siswa suka voli $=5\times7$

Banyak siswa suka voli $=35$ buah.

Banyak siswa yang menyukai olahraga bulu tangkis

Perhatikan bahwa bulu tangkis dalam diagram di atas dinyatakan dalam 3 petak persegi, sehingga banyak siswa yang menyukai bulu bangkis dapat dinyatakan sebagai berikut.

Banyak siswa suka bulu tangkis $=3\times7$

Banyak siswa suka bulu tangkis $=21$ buah.

Sehingga, jumlah siswa yang didata adalah:

Banyak siswa suka sepak bola + basket + voli + bulu tangkis

$=28+42+35+21$

$=126$

Persentase siswa yang suka basket.

$\frac{\text{Banyak}\ \text{Siswa}\ \text{Suka}\ \text{Basket}}{\text{Jumlah}\ \text{Siswa}}\times100\%$

$=\frac{42}{126}\times100\%$

$=0,3333\times100\%$

$=33,33\%$

Jadi, persentase dan banyak siswa yang menyukai basket berturut-turut adalah 33% dan 42 siswa.

Pembahasan:

Diketahui:

Terdapat 13 telepon genggam dalam kondisi baik dan 2 telepon genggam dalam kondisi rusak.

Semua telepon genggam dimasukkan kardus.

Dilakukan pengujian dengan cara mengambil dan menguji satu per satu secara acak tanpa pengembalian.

Ditanya:

Peluang diperoleh 2 telepon genggam rusak pada dua pengujian yang pertama$=?$

Jawab:

Misalkan S adalah ruang sampel dari suatu percobaan dengan tiap anggota S memiliki kesempatan muncul yang sama.

Jika A adalah suatu kejadian dan A adalah himpunan bagian dari S, maka peluang kejadian A adalah

$P\left(A\right)=\frac{n\left(A\right)}{n\left(S\right)}$

dengan

n(A) adalah banyaknya anggota himpunan A

n(S) adalah banyaknya anggota ruang sampel S.

Dalam kasus ini, pada pengambilan pertama dimisalkan $K_1$ yaitu banyak telepon genggam yang rusak, dimisalkan $n\left(A\right)=2,$ sedangkan banyak telepon genggam seluruhnya dimisalkan $n\left(S_1\right)=13+2=15.$ Maka $P\left(A\right)=\frac{n\left(A\right)}{n\left(S_1\right)}=\frac{2}{15}.$

Pada pengembalian kedua dimisalkan $K_2$ yaitu banyak telepon genggam yang rusak menjadi $n\left(B\right)=1,$ sedangkan banyak telepon genggam seluruhnya dimisalkan $n\left(S_2\right)=14.$ Maka $P\left(B\right)=\frac{n\left(B\right)}{n\left(S_2\right)}=\frac{1}{14}.$

Sehingga peluang pada kejadian ini dapat dilakukan mengalikan peluang kejadian $P\left(A\right),\ P\left(B\right)$ dengan memperhatikan bahwa $P\left(B\right)$ adalah kejadian bersyarat dengan syarat kejadian $K_1$.

Diperoleh, peluang terambilnya dua telepon genggam yang rusak satu per satu tanpa pengembalian adalah

$\frac{n\left(A\right)}{n\left(S_1\right)}\cdot\frac{n\left(B\right)}{n\left(S_2\right)}=\frac{2}{15}\cdot\frac{1}{14}=\frac{1}{105}$.

Jadi, $\frac{1}{105}$ adalah peluang terambilnya dua telepon genggam yang rusak satu per satu tanpa pengembalian.

Pembahasan:

Diketahui:

Ukuran lahan parkir = 30m $\times$ 8,5 m

Sudut serong = $30\degree$

Dimensi area parkir untuk satu kendaraan roda empat = 4,8 m $\times$ 2,4 m

Ditanya:

Maksimal banyak kendaraan roda empat yang bisa ditampung di lahan parkir Pak Arief ?

Dijawab:

Pada area parkir serong berikut

Perhatikan segitiga siku-siku $CDE$

Panjang $DE$ dapat dicari menggunakan perbandingan trigonometri

$\frac{DE}{CE}=\cos30\degree$

$\Leftrightarrow DE=4,8\times\frac{1}{2}\sqrt{3}=2,4\sqrt{3}\approx4,16$ m

Untuk mengetahui banyak mobil yang dapat ditampung di lahan parkir tersebut, kita dapat membagi panjang lahan parkir yaitu 30 m dengan panjang $DE$

Banyak mobil = $\frac{30}{4,16}=7,2115...$

banyak mobil dibulatkan ke bawah ke satuan terdekat yaitu 7 mobil.

Jadi, maksimal banyak mobil yang bisa ditampung adalah 7 mobil.

Pembahasan:

Diketahui:

• Panjang awalan dan akhiran ramp masing-masing dapat dibuat 1,2 m hingga 1,5 m
• Sudut kemiringan single ramp dengan tinggi ramp maksimum 76 cm yang direkomendasikan adalah $3,6°-4,8°$

Ditanya:

Panjang area yang cukup digunakan untuk membuat single ramp yang tingginya 76 cm lengkap dengan awalan dan akhiran?

Dijawab:

Perhatikan kalau semua opsi jawabannya memuat tanda lebih besar dari. Artinya angka panjang area yang perlu dicari adalah panjang terpendek yang cukup untuk membuat single ramp lengkap dengan awalan dan akhiran.

Panjang dataran, yaitu ramp tanpa awalan dan akhiran, dapat dicari menggunakan rumus:

Ukuran dataran ramp=tanαtinggi ramp​  

Dari rumus di atas, diketahui:

Panjang dataran single ramp semakin pendek jika nilai tangen semakin besar. Nilai tangen terbesar  diperoleh jika sudut kemiringan yang digunakan juga terbesar, yaitu $4,8°$.

Panjang dataran terpendek:

Ukuran dataran ramp=tan4,8∘76​    

$=\frac{\text{76}}{0,084\ }\$

$=905$ cm

$=9,05$ meter

Area terpendek untuk membuat single ramp dengan awalan dan akhiran:

= Ukuran awalan terpendek + ukuran dataran terpendek + ukuran akhiran terpendek

= 1,2 + 9,05 + 1,2

= 11,45 m

Panjang area yang cukup digunakan untuk membuat single ramp yang tingginya 76 cm:

Panjang area yang cukup $\ge$ 11,45 m

Jadi, panjang area yang cukup digunakan untuk membuat single ramp yang tingginya 76 cm lengkap dengan awalan dan akhiran berukuran $\ge$ 11,45 meter.