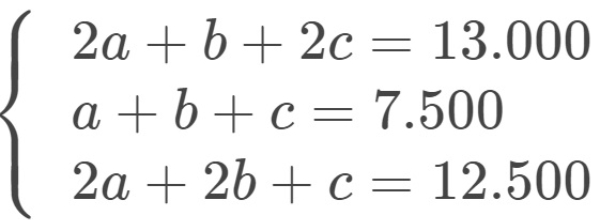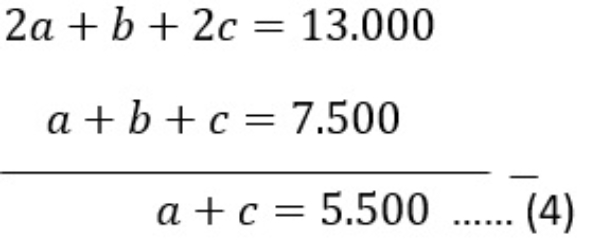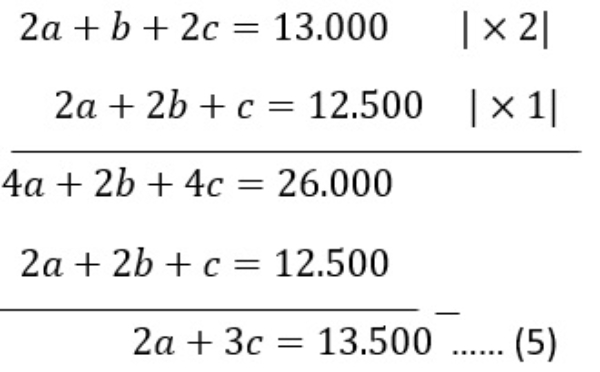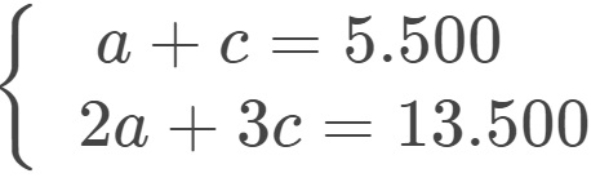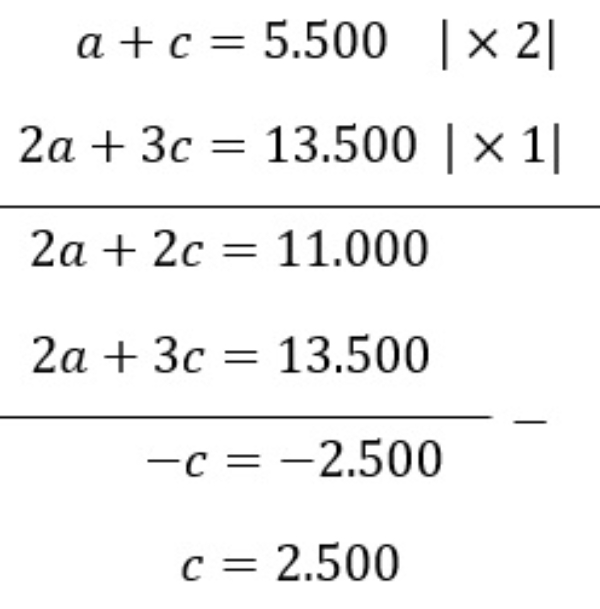Bank Soal Matematika SMA Sistem Persamaan Linear Tiga Variabel
Soal
Level 5 Pemahaman Menghitung Matematika Wajib LOTS Soal Cerita
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Septian melihat fenomena alam seperti embun yang menjadi es pada dataran tinggi Dieng. Jika Septian akan melakukan penelitian tentang fenomena ini, berikut beberapa pertanyaan yang sesuai, kecuali ...
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Kerja Ilmiah dan Metode Ilmiah
Choose the correct answer.
Mr. Eddie ... (not/watch) a football match right now.
Bahasa Inggris
Level 10
Congratulating and Complimenting
Tenses: Simple Present & Present Continuous
Dari sekian banyak aturan keselamatan kerja di laboratorium, salah satunya adalah siswa tidak diperbolehkan membawa makanan atau minuman ke dalam laboratorium. Apa alasan yang tepat terkait aturan tersebut?
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Keselamatan Kerja di Laboratorium
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tingkat Keanekaragaman Hayati
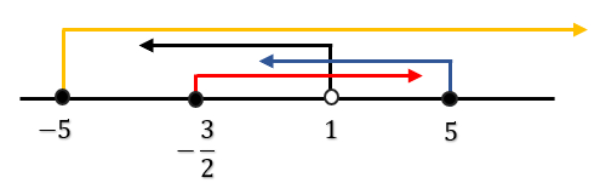
EDIT: bisa ditambahkan garis bilangan yang diarsir yang dimaksud di pembahasan
Himpunan penyelesaian yang sesuai dengan garis bilangan berikut adalah ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Pertidaksamaan Linear Satu Variabel
Yang dimaksud dengan tuyang adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Interpretasi dan Analisis Teks Laporan Hasil Observasi
Pada lahan pertanian sering terjadi kompetisi antara rumput dengan tanaman padi ladang. Berikut ini cara yang paling tepat untuk menghilangkan atau meminimalisir kompetisi antara kedua spesies tersebut adalah ....
Biologi
Level 10
Biologi
Ekologi
Interaksi Antarkomponen di Ekosistem
Perhatikan jenis virus berikut!
- Virus rabies
- Bakteriofag
- Virus flu burung
- Human Immunodeficiency Virus
Dari daftar di atas, virus yang memiliki kisaran inang yang cukup luas adalah ....
Biologi
Level 10
Biologi
Virus
Cara Hidup dan Reproduksi Virus
Dalam melaksanakan metode ilmiah, terkadang kesimpulan yang didapatkan tidaklah sesuai dengan hipotesis awal yang telah dibuat. Untuk itu, hal yang harus dilakukan adalah ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Metode Ilmiah dan Laboratorium Kimia
Diketahui
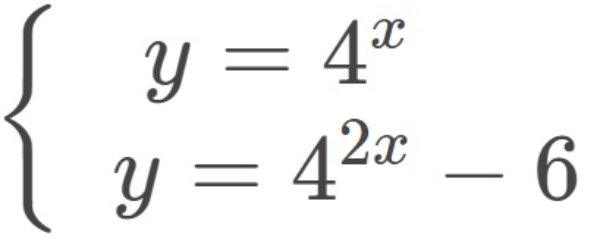
Himpunan penyelesaian untuk sistem persamaan dua variabel di atas adalah ....
Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Sistem Persamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Septian melihat fenomena alam seperti embun yang menjadi es pada dataran tinggi Dieng. Jika Septian akan melakukan penelitian tentang fenomena ini, berikut beberapa pertanyaan yang sesuai, kecuali ...
Choose the correct answer.
Mr. Eddie ... (not/watch) a football match right now.
Dari sekian banyak aturan keselamatan kerja di laboratorium, salah satunya adalah siswa tidak diperbolehkan membawa makanan atau minuman ke dalam laboratorium. Apa alasan yang tepat terkait aturan tersebut?
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
EDIT: bisa ditambahkan garis bilangan yang diarsir yang dimaksud di pembahasan
Himpunan penyelesaian yang sesuai dengan garis bilangan berikut adalah ....
Yang dimaksud dengan tuyang adalah ….
Pada lahan pertanian sering terjadi kompetisi antara rumput dengan tanaman padi ladang. Berikut ini cara yang paling tepat untuk menghilangkan atau meminimalisir kompetisi antara kedua spesies tersebut adalah ....
Perhatikan jenis virus berikut!
- Virus rabies
- Bakteriofag
- Virus flu burung
- Human Immunodeficiency Virus
Dari daftar di atas, virus yang memiliki kisaran inang yang cukup luas adalah ....
Dalam melaksanakan metode ilmiah, terkadang kesimpulan yang didapatkan tidaklah sesuai dengan hipotesis awal yang telah dibuat. Untuk itu, hal yang harus dilakukan adalah ....
Diketahui
Himpunan penyelesaian untuk sistem persamaan dua variabel di atas adalah ....