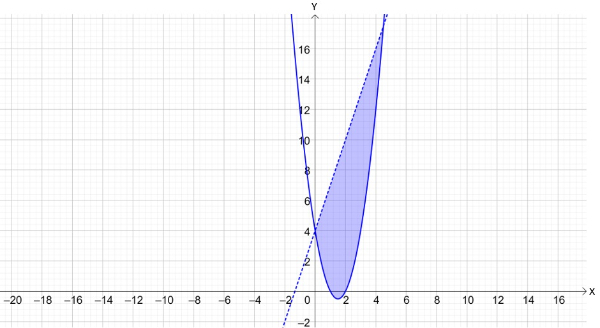
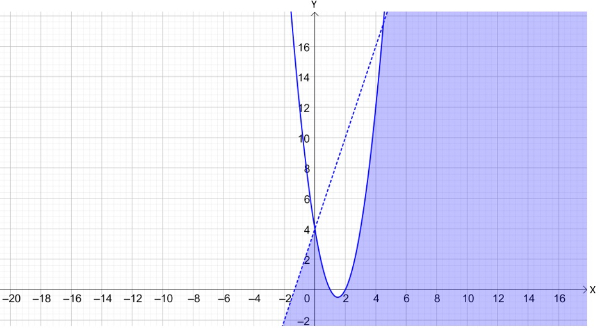
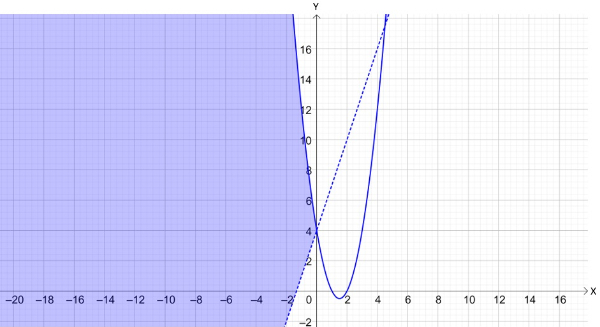
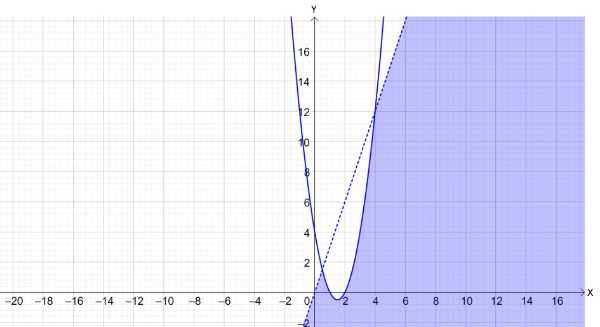
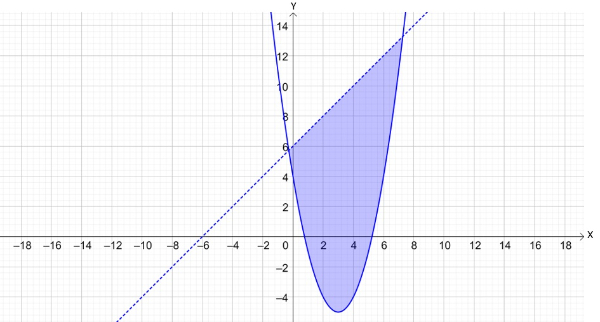
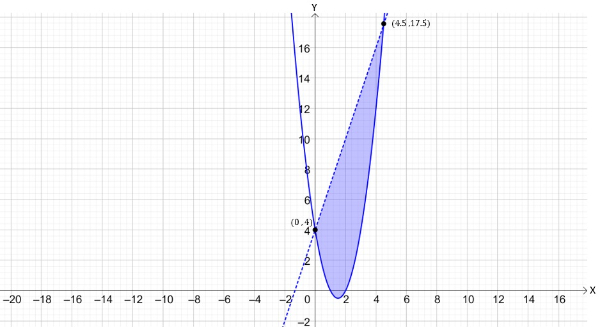
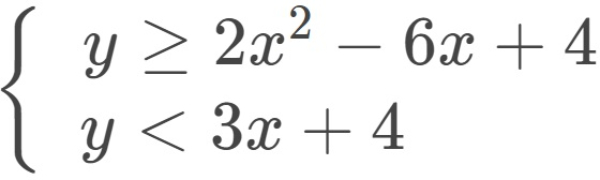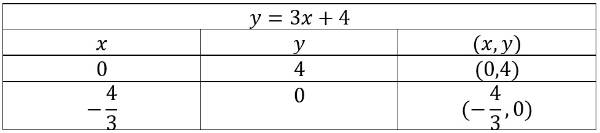Bank Soal Matematika SMA Sistem Pertidaksamaan Dua Variabel
Soal
Matematika Wajib LOTS Teknik Hitung
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
9.200 dibaca ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Membilang Sampai 10.000
Perhatikan gambar di bawah ini!

(Sumber: www.startfmmadina.com)
Kegunaan benda gas di atas adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menggali Informasi Konsep Perubahan Wujud Benda
Berikut adalah data jenis buah kesukaan 20 siswa kelas III.

Diagram batang berikut yang sesuai dengan data di atas adalah ...
Matematika
Level 3
Statistika
Data
Mengumpulkan dan Menyajikan Data
Perhatikan denah berikut!
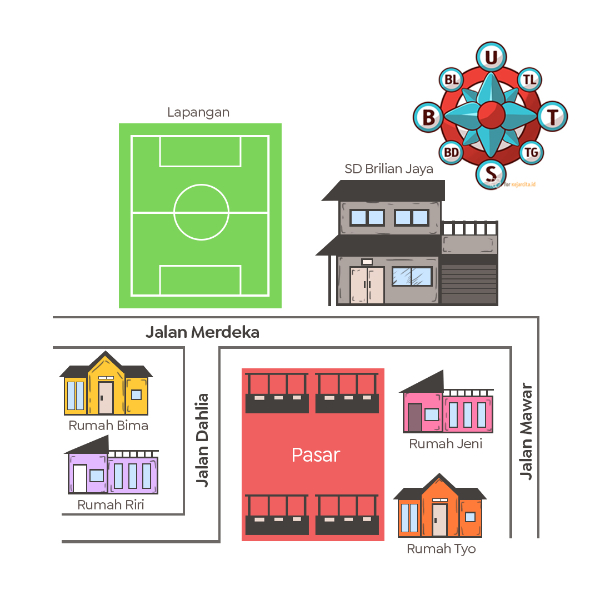
Rumah Riri berada di sebelah barat Jalan Dahlia. Rumah Bima berada di ... rumah Riri.
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
....
Matematika
Level 3
Bilangan
Pecahan Sederhana
Penjumlahan Pecahan Penyebut Sama
Anis akan mengukur panjang pensil warna miliknya dengan menggunakan penggaris.

(Sumber: freepik.com)
Panjang pensil Anis adalah ....
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Alat Ukur Panjang
Panjang persegi panjang 8 cm. Luas persegi panjang tersebut 40 cm2. Keliling persegi panjang ... cm.
Matematika
Level 3
Geometri
Bangun Datar
Keliling dan Luas Bangun Datar
Sebuah mobil tangki membawa bahan bakar kendaraan.

Volume bahan bakar yang dibawa mobil tangki tersebut adalah ....
Matematika
Level 3
Geometri
Volume Bangun Ruang
Volume Bangun Ruang
144 12 = ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Operasi Hitung Bilangan Cacah
Percakapan antara dua orang atau lebih yang berlangsung antara narasumber dan pewawancara disebut ....
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menggali Informasi melalui Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
9.200 dibaca ....
Perhatikan gambar di bawah ini!

(Sumber: www.startfmmadina.com)
Kegunaan benda gas di atas adalah ....
Berikut adalah data jenis buah kesukaan 20 siswa kelas III.
Diagram batang berikut yang sesuai dengan data di atas adalah ...
Perhatikan denah berikut!
Rumah Riri berada di sebelah barat Jalan Dahlia. Rumah Bima berada di ... rumah Riri.
....
Anis akan mengukur panjang pensil warna miliknya dengan menggunakan penggaris.
(Sumber: freepik.com)
Panjang pensil Anis adalah ....
Panjang persegi panjang 8 cm. Luas persegi panjang tersebut 40 cm2. Keliling persegi panjang ... cm.
Sebuah mobil tangki membawa bahan bakar kendaraan.
Volume bahan bakar yang dibawa mobil tangki tersebut adalah ....
144 12 = ….
Percakapan antara dua orang atau lebih yang berlangsung antara narasumber dan pewawancara disebut ....