Bank Soal Matematika SMA Aplikasi Rasio Trigonometri
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Budi memiliki sebuah bambu sepanjang m. Karena terlalu panjang, bambu itu dipotong dan dibuang m . Panjang bambu itu sekarang adalah ...
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Berikut ini yang tidak termasuk ciri iklan baris yaitu ....
Bahasa Indonesia
Level 5
Membaca
Iklan
Jenis-jenis Iklan
Jarak rumah Ridho ke sekolah 4,5 km. Dengan menaiki sepeda ia membutuhkan waktu 15 menit. Kecepatan Ridho dalam mengayuh sepeda yaitu …
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Kecepatan
Bagian tanah yang mencapai tinggi 600 meter di atas permukaan laut dan menyerupai kerucut disebut ....
IPS
Level 5
Geografi
Karakteristik Geografi Wilayah Indonesia
Kondisi Wilayah Indonesia
Read the following dialogue and answer the question.

Mom: Son, this is our new neighbor, Jenny.
Aiden: Hey, Jenny.
Jenny: Hello. What is your name?
Aiden: I'm Aiden.
Jenny: Can you spell it?
Aiden: ….
Which spelling is correct to complete the dialogue?
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Spelling
Perhatikan gambar berikut!
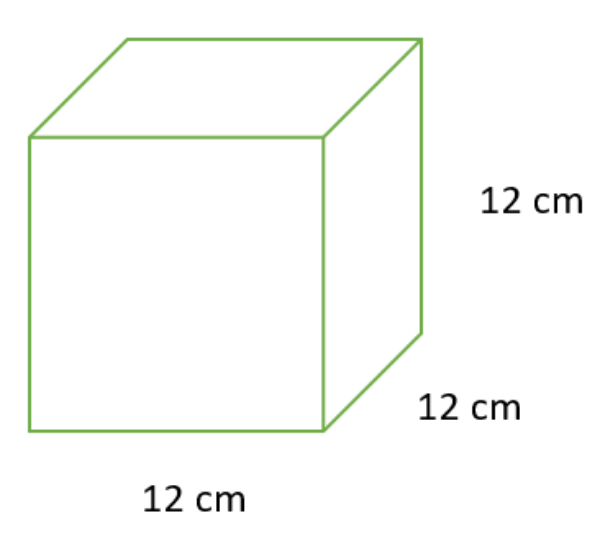
Volume bangun tersebut adalah ... cm3
Matematika
Level 5
Geometri
Balok dan Kubus
Volume Balok dan Kubus
Berikut diagram batang yang menunjukkan jarak sekolah dengan rumah 6 siswa.
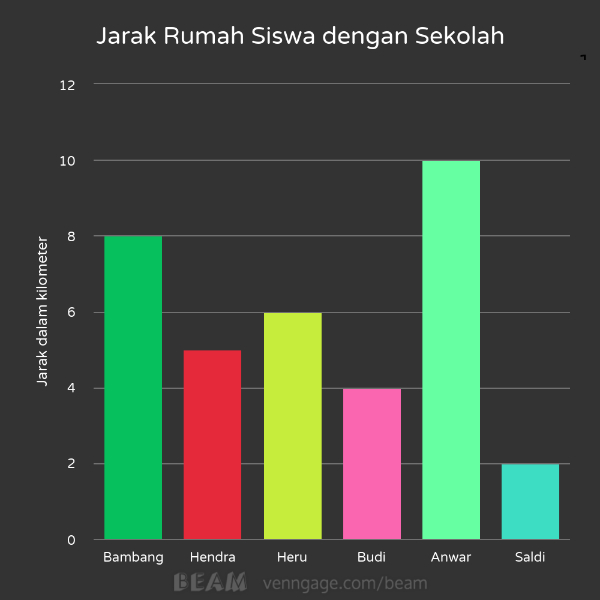
Siapakah siswa yang rumahnya paling dekat dengan sekolah?
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data

Berdasarkan diagram di atas, berapakah jumlah siswa yang memiliki tinggi 136 cm?
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Ide pokok paragraf ketiga adalah ....
Bahasa Indonesia
Level 5
Membaca
Teks Eksplanasi
Struktur Teks Eksplanasi

Berikut ini merupakan contoh surat undangan ....
Bahasa Indonesia
Level 5
Membaca
Surat Undangan
Identifikasi Surat Undangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Budi memiliki sebuah bambu sepanjang m. Karena terlalu panjang, bambu itu dipotong dan dibuang m . Panjang bambu itu sekarang adalah ...
Berikut ini yang tidak termasuk ciri iklan baris yaitu ....
Jarak rumah Ridho ke sekolah 4,5 km. Dengan menaiki sepeda ia membutuhkan waktu 15 menit. Kecepatan Ridho dalam mengayuh sepeda yaitu …
Bagian tanah yang mencapai tinggi 600 meter di atas permukaan laut dan menyerupai kerucut disebut ....
Read the following dialogue and answer the question.

Mom: Son, this is our new neighbor, Jenny.
Aiden: Hey, Jenny.
Jenny: Hello. What is your name?
Aiden: I'm Aiden.
Jenny: Can you spell it?
Aiden: ….
Which spelling is correct to complete the dialogue?
Perhatikan gambar berikut!
Volume bangun tersebut adalah ... cm3
Berikut diagram batang yang menunjukkan jarak sekolah dengan rumah 6 siswa.
Siapakah siswa yang rumahnya paling dekat dengan sekolah?
Berdasarkan diagram di atas, berapakah jumlah siswa yang memiliki tinggi 136 cm?
Ide pokok paragraf ketiga adalah ....
Berikut ini merupakan contoh surat undangan ....



