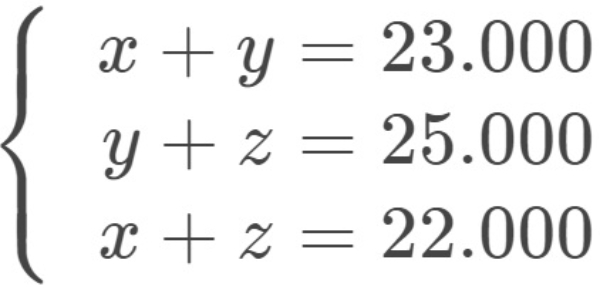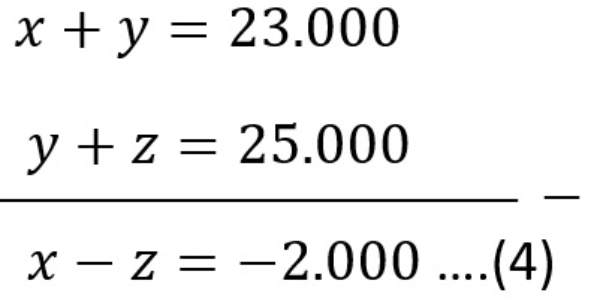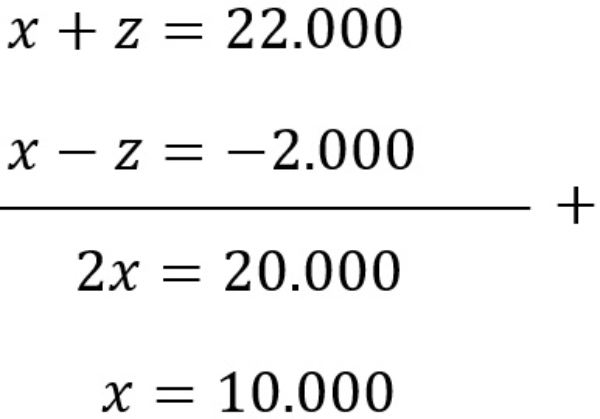Bank Soal Matematika SMA Sistem Persamaan Linear Tiga Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Pak Budi memiliki sebuah peternakan ayam.
Mula-mula, ayam yang ada di peternakan pak Budi berjumlah 375 ekor.
Karena air yang tercemar, ayam-ayam di peternakan Pak Budi mati 143 ekor.
Sisa ayam yang ada di peternakan Pak Budi saat ini ada ... ekor.
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Penjumlahan dan Pengurangan Bilangan Sampai 999
Hormatilah orang tuamu di rumah dan gurumu di sekolah!
Kalimat di atas merupakan ungkapan ....
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Perintah
Gambar yang tepat untuk melanjutkan pola barisan berikut ini adalah ....

(Sumber: freepik.com)
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Pola Barisan Bangun Ruang
Asa pergi ke toko.
Di toko tersebut menjual berbagai macam alat tulis.
Berikut adalah daftar harga berbagai macam alat tulis yang dijual.

(Sumber Gambar: flaticon.com)
Asa memiliki 1 lembar uang dua ribuan.
Ia ingin menggunakan uangnya untuk membeli 2 jenis barang tetapi masih mendapatkan uang kembalian.
Barang yang dapat dibeli Asa adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Perhatikan gambar berikut!!

(Sumber Gambar: freepik.com)
Banyaknya segi enam pada gambar di atas ada ... buah.
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Ciri-Ciri Bangun Datar Sederhana
Perhatikan gambar berikut!


(Sumber Gambar: id.wikipedia.org)
Pecahan uang yang setara dengan uang pada gambar di atas adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Arrange the jumbled letters.

Source: canva
Bahasa Inggris
Level 2
A NEW FRIEND
Shape and Colour

Sumber: freepik.com
Perhatikan gambar diatas.
Jika tinggi Yudi 115 cm, maka tinggi Tyas adalah ... cm.
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Panjang
Hal yang tidak perlu diperhatikan saat membaca puisi adalah ....
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Lafal, Intonasi, dan Ekspresi dalam Membaca Puisi
Di taman terdapat beberapa kumbang seperti pada gambar.
Kumbang-kumbang tersebut ada yang terbang dan ada yang masih hinggap di dedaunan maupun bunga.

(Sumber: freepik.com)
Bilangan pecahan yang menyatakan jumlah kumbang yang terbang adalah ....
Matematika
Level 2
Bilangan
Konsep Pecahan
Konsep Pecahan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pak Budi memiliki sebuah peternakan ayam.
Mula-mula, ayam yang ada di peternakan pak Budi berjumlah 375 ekor.
Karena air yang tercemar, ayam-ayam di peternakan Pak Budi mati 143 ekor.
Sisa ayam yang ada di peternakan Pak Budi saat ini ada ... ekor.
Hormatilah orang tuamu di rumah dan gurumu di sekolah!
Kalimat di atas merupakan ungkapan ....
Gambar yang tepat untuk melanjutkan pola barisan berikut ini adalah ....
(Sumber: freepik.com)
Asa pergi ke toko.
Di toko tersebut menjual berbagai macam alat tulis.
Berikut adalah daftar harga berbagai macam alat tulis yang dijual.
(Sumber Gambar: flaticon.com)
Asa memiliki 1 lembar uang dua ribuan.
Ia ingin menggunakan uangnya untuk membeli 2 jenis barang tetapi masih mendapatkan uang kembalian.
Barang yang dapat dibeli Asa adalah ....
Perhatikan gambar berikut!!
(Sumber Gambar: freepik.com)
Banyaknya segi enam pada gambar di atas ada ... buah.
Perhatikan gambar berikut!
(Sumber Gambar: id.wikipedia.org)
Pecahan uang yang setara dengan uang pada gambar di atas adalah ....
Arrange the jumbled letters.
Source: canva
Sumber: freepik.com
Perhatikan gambar diatas.
Jika tinggi Yudi 115 cm, maka tinggi Tyas adalah ... cm.
Hal yang tidak perlu diperhatikan saat membaca puisi adalah ....
Di taman terdapat beberapa kumbang seperti pada gambar.
Kumbang-kumbang tersebut ada yang terbang dan ada yang masih hinggap di dedaunan maupun bunga.
(Sumber: freepik.com)
Bilangan pecahan yang menyatakan jumlah kumbang yang terbang adalah ....