Bank Soal Matematika SMA Sistem Pertidaksamaan Dua Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Jenis polisakarida yang terdapat pada sel otot dan hati hewan serta berperan sebagai cadangan makanan adalah ....
Biologi
Level 11
Biologi
Sel
Penemuan, Tipe, Ukuran, dan Komponen Kimiawi Sel
Why does Elsa can’t study seriously?
Bahasa Inggris
Level 11
Good Advice
Giving Advice or Suggestions
Jika titik ditranslasikan oleh 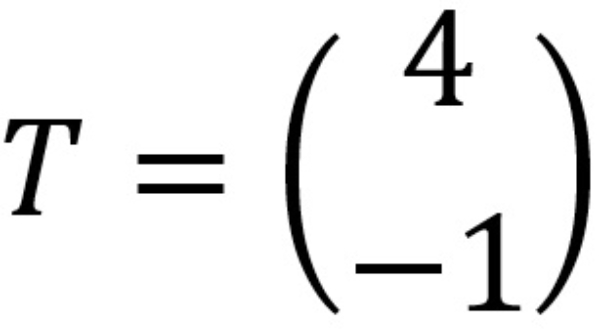 maka bayangan titik adalah ....
maka bayangan titik adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
Berikut ini yang merupakan contoh yang serupa dengan konsep induksi matematika adalah ....
Matematika
Level 11
Logika
Induksi Matematika
Konsep dan Prinsip Induksi Matematika
Pada tekanan yang sama suatu senyawa heksuna memiliki titik didih 100 0C sedangkan senyawa propuna memiliki titik didih sebesar -23 0C. Penyebab dari perbedaan titik didih antar sesama senyawa alkuna tersebut adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Terdapat 3 buah partikel yang berada di titik koordinat berikut.

Partikel A dan B masing-masing bermassa 1 kg sementara partikel C bermassa 2 kg. Besar momen inersia sistem jika ketiga partikel diputar terhadap sumbu y adalah ....
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Dinamika Benda Tegar
Membran sel bersifat impermeabel terhadap molekul di bawah ini, kecuali ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Nama senyawa dari struktur di bawah ini adalah ....
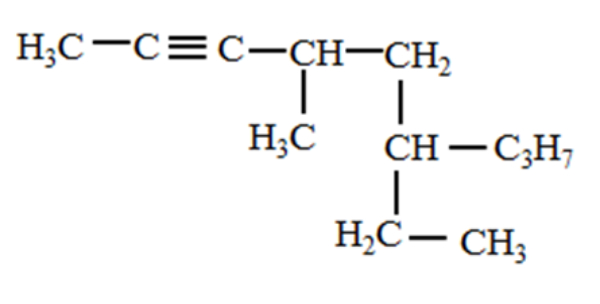
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Jika dan adalah solusi dari persamaan trigonometri untuk dan maka nilai dari
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Berikut adalah gas-gas yang ada di udara.
-
-
-
-
Gas penyebab efek rumah kaca adalah ....
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Jenis polisakarida yang terdapat pada sel otot dan hati hewan serta berperan sebagai cadangan makanan adalah ....
Why does Elsa can’t study seriously?
Jika titik ditranslasikan oleh 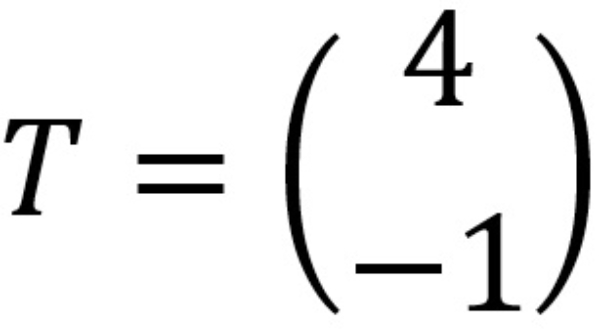
Berikut ini yang merupakan contoh yang serupa dengan konsep induksi matematika adalah ....
Pada tekanan yang sama suatu senyawa heksuna memiliki titik didih 100 0C sedangkan senyawa propuna memiliki titik didih sebesar -23 0C. Penyebab dari perbedaan titik didih antar sesama senyawa alkuna tersebut adalah ....
Terdapat 3 buah partikel yang berada di titik koordinat berikut.
Partikel A dan B masing-masing bermassa 1 kg sementara partikel C bermassa 2 kg. Besar momen inersia sistem jika ketiga partikel diputar terhadap sumbu y adalah ....
Membran sel bersifat impermeabel terhadap molekul di bawah ini, kecuali ....
Nama senyawa dari struktur di bawah ini adalah ....
Jika dan adalah solusi dari persamaan trigonometri untuk dan maka nilai dari
Berikut adalah gas-gas yang ada di udara.
-
-
-
-
Gas penyebab efek rumah kaca adalah ....



