Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Dua buah uang logam dilempar secara bersama-sama sebanyak 48 kali. Berapa frekuensi harapan muncul 2 gambar?
Matematika
Level 8
Statistika
Peluang
Frekuensi Harapan
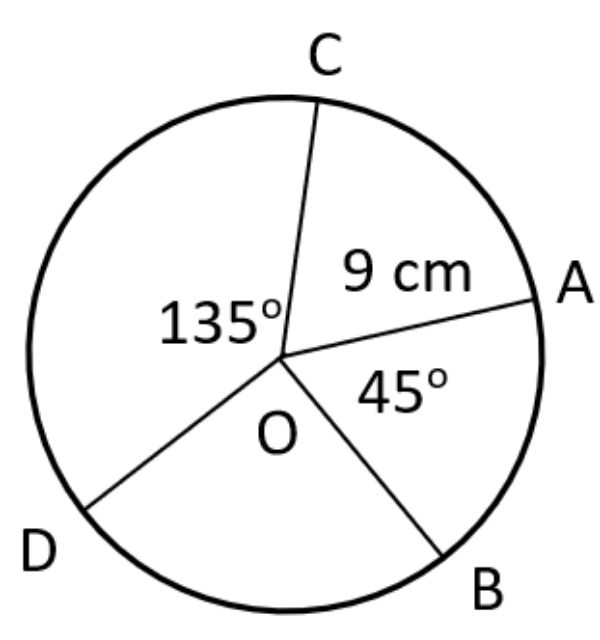
Jika panjang busur AB adalah 15 cm, maka panjang busur CD adalah ... cm
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
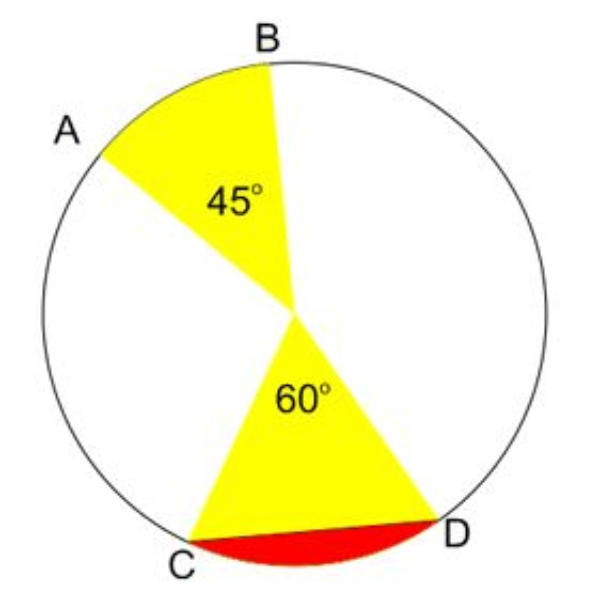
Perhatikan gambar lingkaran di atas, apabila panjang busur AB = 33 cm dan luas juring COD = 924 cm2, maka tentukanlah panjang busur CD!
Matematika
Level 8
Geometri
Lingkaran
Adit, Baba, Cahyo, dan Dedi tengah duduk di sebuah bangku pada suatu lorong. Adit duduk di posisi kedua dari kanan dan bersebelahan dengan Baba. Cahyo dan Dedi masing-masing berada diposisi ujung bangku. Jika Cahyo dan Baba mengapit Adit, maka ketika Ella datang, dimanakah posisi Ella saat duduk dibangku yang sama?
Matematika
Level 8
Geometri
Koordinat Kartesius
Bacalah paragraf di bawah!
Kebakaran hutan yang terjadi di Kalimantan beberapa pekan lalu kembali terjadi pada Senin (19/02/2020). Diduga kebakaran tersebut terjadi karena adanya oknum-oknum yang sengaja membuang puntung rokok yang masih menyala di dalam hutan. Ranting-ranting kering dan musim kemarau yang tidak kunjung berakhir menambah faktor pendukung penyebab kebakaran hutan kemarin.
Pernyataan yang sesuai dengan paragraf berita di atas adalah ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Simpulan Isi Berita
- This chair is as comfortable as a sofa.
- Mark plays the piano as well as his mother does.
- My brother drives a car as carefully as I do.
- Your bag is just as stylish as the one in a magazine.
- Emma is as popular as Rachel.
- I exercise as often as you do.
Which sentence numbers show comparative adverbs?
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Segitiga siku-siku SRQ digambar pada bidang koordinat sebagai berikut :
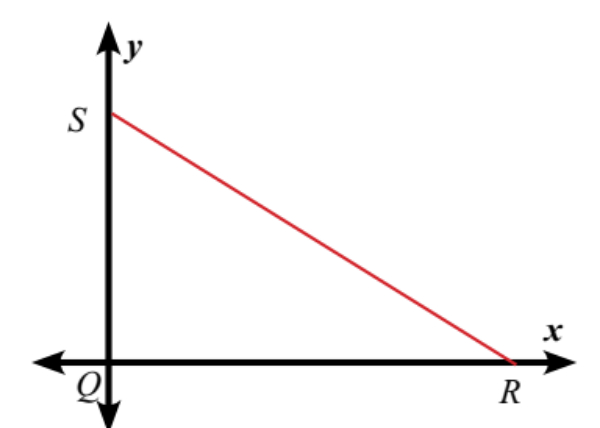
Jika panjang QR adalah 7 satuan dan panjang QS adalah 5 satuan, maka titik-titik koordinat Q, R, dan S secara berurutan adalah?
Matematika
Level 8
Geometri
Koordinat Kartesius
Posisi Titik terhadap Titik Tertentu
Perbedaan makna konotasi dan makna denotasi dalam puisi adalah ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Perhatikan gambar berikut!

Apa pesan yang disampaikan dalam iklan tersebut?
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Simpulan Isi Iklan, Slogan, Poster
You are about going to the bookstore to buy some novels. Suddenly, you meet your classmate on the way you go to the bookstore. You want to ask him whether he is willing to come with you to the bookstore or not. You may say ....
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Willingness to Do Something
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Dua buah uang logam dilempar secara bersama-sama sebanyak 48 kali. Berapa frekuensi harapan muncul 2 gambar?
Jika panjang busur AB adalah 15 cm, maka panjang busur CD adalah ... cm
Perhatikan gambar lingkaran di atas, apabila panjang busur AB = 33 cm dan luas juring COD = 924 cm2, maka tentukanlah panjang busur CD!
Adit, Baba, Cahyo, dan Dedi tengah duduk di sebuah bangku pada suatu lorong. Adit duduk di posisi kedua dari kanan dan bersebelahan dengan Baba. Cahyo dan Dedi masing-masing berada diposisi ujung bangku. Jika Cahyo dan Baba mengapit Adit, maka ketika Ella datang, dimanakah posisi Ella saat duduk dibangku yang sama?
Bacalah paragraf di bawah!
Kebakaran hutan yang terjadi di Kalimantan beberapa pekan lalu kembali terjadi pada Senin (19/02/2020). Diduga kebakaran tersebut terjadi karena adanya oknum-oknum yang sengaja membuang puntung rokok yang masih menyala di dalam hutan. Ranting-ranting kering dan musim kemarau yang tidak kunjung berakhir menambah faktor pendukung penyebab kebakaran hutan kemarin.
Pernyataan yang sesuai dengan paragraf berita di atas adalah ....
- This chair is as comfortable as a sofa.
- Mark plays the piano as well as his mother does.
- My brother drives a car as carefully as I do.
- Your bag is just as stylish as the one in a magazine.
- Emma is as popular as Rachel.
- I exercise as often as you do.
Which sentence numbers show comparative adverbs?
Segitiga siku-siku SRQ digambar pada bidang koordinat sebagai berikut :
Jika panjang QR adalah 7 satuan dan panjang QS adalah 5 satuan, maka titik-titik koordinat Q, R, dan S secara berurutan adalah?
Perbedaan makna konotasi dan makna denotasi dalam puisi adalah ....
Perhatikan gambar berikut!
Apa pesan yang disampaikan dalam iklan tersebut?
You are about going to the bookstore to buy some novels. Suddenly, you meet your classmate on the way you go to the bookstore. You want to ask him whether he is willing to come with you to the bookstore or not. You may say ....



