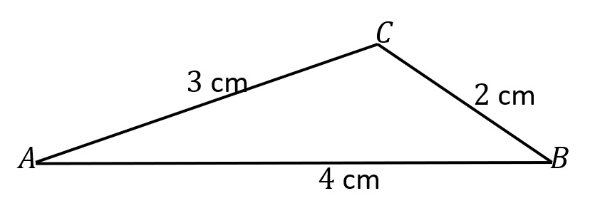
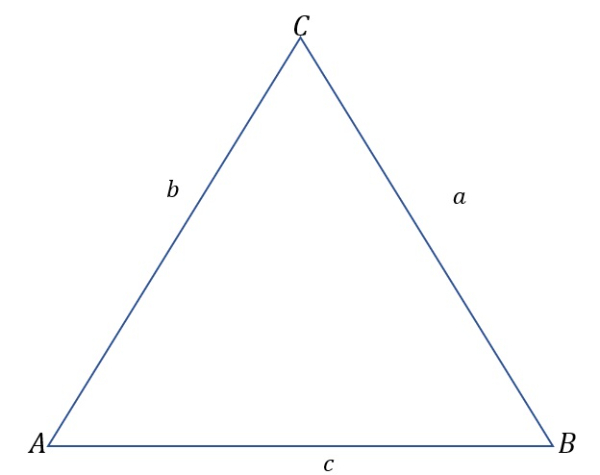
Bank Soal Matematika Wajib SMA Aturan Cosinus

Soal

Pilihan Ganda

Perhatikan gambar berikut

cos⁡A=....\cos A=....

A

cos⁡A=32+42−222.3.4\cos A=\frac{3^2+4^2-2^2}{2.3.4}

B

cos⁡A=42+32−422.3.4\cos A=\frac{4^2+3^2-4^2}{2.3.4}

C

cos⁡A=22+42−323.3.4\cos A=\frac{2^2+4^2-3^2}{3.3.4}

D

cos⁡A=32+42+222.3.4\cos A=\frac{3^2+4^2+2^2}{2.3.4}

E

cos⁡A=22+42+322.2.4\cos A=\frac{2^2+4^2+3^2}{2.2.4}

Pembahasan:

Persoalan di atas dapat diselesaikan dengan aturan cosinus.

Jika diketahui segitiga sembarang sebagai berikut

maka berlaku aturan cosinus

cos⁡A=b2+c2−a22bc\cos A=\frac{b^2+c^2-a^2}{2bc}

cos⁡B=a2+c2−b22ac\cos B=\frac{a^2+c^2-b^2}{2ac}

cos⁡C=a2+b2−c22ab\cos C=\frac{a^2+b^2-c^2}{2ab}

Dengan demikian, pada persoalan di atas a=2a=2 cm, b=3b=3 cm, dan c=4c=4 cm. Maka nilai cos⁡A\cos A adalah

cos⁡A=b2+c2−a22bc\cos A=\frac{b^2+c^2-a^2}{2bc}

cos⁡A=32+42−222.3.4\cos A=\frac{3^2+4^2-2^2}{2.3.4}

Video
04 Januari 2021
Penerapan Barisan dan Deret dalam Kehidupan
✔ Ingin tanya tutor?
✔ Cek sampel tanya jawab
Rangkuman
27 April 2021
Persamaan dan Pertidaksamaan Nilai Mutlak | Matematika | Kelas 10 | KD 3.1 & KD 4.1
Selengkapnya
Lihat Semua Rangkuman dan Materi

Siswa

Ingin latihan soal, nonton, atau unduh materi belajar lebih banyak?

Buat Akun Gratis

Guru

Ingin akses bank soal, nonton, atau unduh materi belajar lebih banyak?

Buat Akun Gratis

Soal Populer Hari Ini

Bacalah paragraf di bawah!

Kebakaran hutan yang terjadi di Kalimantan beberapa pekan lalu kembali terjadi pada Senin (19/02/2020). Diduga kebakaran tersebut terjadi karena adanya oknum-oknum yang sengaja membuang puntung rokok yang masih menyala di dalam hutan. Ranting-ranting kering dan musim kemarau yang tidak kunjung berakhir menambah faktor pendukung penyebab kebakaran hutan kemarin.


Pernyataan yang sesuai dengan paragraf berita di atas adalah ....

Bahasa Indonesia Level 8 Menulis Teks Berita Simpulan Isi Berita KD4.1 Kelas VIII Kurikulum 2013 K13 Bahasa Indonesia
Lihat selengkapnya

Jika titik P(−6,10)P\left(-6,10\right) dan Q(−4,10)Q\left(-4,10\right) , maka koordinat posisi titik QQ terhadap titik PP adalah ....

Matematika Level 8 Geometri Koordinat Kartesius Koordinat Posisi Suatu Benda Kelas VIII Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Source: depositphotos.com

Which sentence best describes the picture?

Bahasa Inggris Level 8 Bahasa Inggris Existence of things and people around us Expression of existence Kelas VIII Kurikulum 2013 K13
Lihat selengkapnya

Look at the table below.

Source: canva.com

Make sentences with 'can' or 'can't' with the verbs in the brackets and join them with 'and' or 'but.'

A. Kelly (cook/dance)

B. Andy (sing/type)

C. John (cook/ski)

Which one is the most suitable statement for point A?

Bahasa Inggris Level 8 Bahasa Inggris Interaction among students inside and outside classrooms Expressions of Explaining Abilities Expressions of explaining ability Kelas VIII Kurikulum 2013 K13
Lihat selengkapnya

Pertandingan sepak bola antara klub PSMS Medan dengan klub Semen Padang akan diselenggarakan di Stadion Teladan. Tiket khusus VIP telah terjual sebanyak 450 tiket. Panitia menetapkan harga tiket untuk pelajar adalah Rp. 20.000, dan harga tiket untuk orang dewasa adalah Rp. 45.000. Total pendapatan yang diterima panitia dari penjualan tiket tersebut adalah Rp. 15.950.000. Berapakah masing-masing jumlah tiket yang terjual untuk pelajar dan orang dewasa?

Matematika Level 8 Aljabar Sistem Persamaan Linear Dua Variabel (SPLDV) Menyelesaikan SPLDV Kelas VIII Level 4 Pemahaman Menghitung Kurikulum 2013 K13 Matematika
Lihat selengkapnya

The correct quantifier that describes the illustration above is ….

Bahasa Inggris Level 8 Bahasa Inggris Existence of things and people around us Quantifiers for Countable & Uncountable Nouns Kelas VIII Kurikulum 2013 K13
Lihat selengkapnya

Read the following description of Michelle’s living room.

Source: freepik.com

This is Michelle’s living room. (1) There aren’t many furnitures in it because she likes to keep everything clean and tidy. (2) There are only a small cabinet, a big yellow couch, and a single sofa chair to sit with her family. Her cat would also rest on the couch because it is very comfortable. (3) There is no painting on the wall but Michelle prefers to add green plants to the decoration. They become new trends lately and her favorite is definitely a palm leaf. (4) There are also books on the wall. She usually reads them while enjoying a nice cup of tea in the morning. 

Which of the sentence numbers above is not grammatically correct?

Bahasa Inggris Level 8 Bahasa Inggris Existence of things and people around us Expression of existence Kelas VIII Kurikulum 2013 K13
Lihat selengkapnya

Look at the following picture.

Source: petmd.com

What will you do if you see this?

Bahasa Inggris Level 8 Bahasa Inggris Interaction among students inside and outside classrooms Expressions of Willingness to Do Something Kelas VIII Kurikulum 2013 K13
Lihat selengkapnya

Perhatikan pernyataan di bawah ini!

  1. Menjaga berat badan normal sesuai indeks massa tubuh
  2. Tidak mengonsumsi minuman beralkohol
  3. Ikut program vaksinasi hepatitis
  4. Rajin mengonsumsi air putih

Pernyataan di atas merupakan upaya yang dapat dilakukan untuk menjaga kesehatan sistem ekskresi pada organ ....

IPA Level 8 Biologi Sistem Ekskresi Upaya Menjaga Kesehatan Sistem Eskresi Kelas VIII Sistem Ekskresi Kurikulum 2013 K13 IPA
Lihat selengkapnya

Diketahui BC = 12 cm, CD = 9 cm dan luas △ABD\triangle ABD = 150 cm2. Tentukan panjang AB!

Matematika Level 8 Geometri Teorema Pythagoras Segitiga dan Teorema Pythagoras Kelas VIII Kurikulum 2013 K13 Matematika
Lihat selengkapnya
✔ Ingin soal latihan HOTS?
✔ Cek sampel soal HOTS?

Cek Contoh Kuis Online

Kejar Kuis

Cek Contoh Bank Soal

Kejar Soal