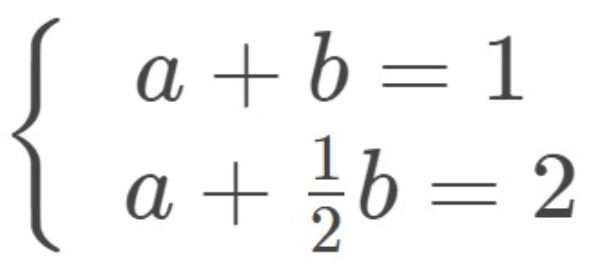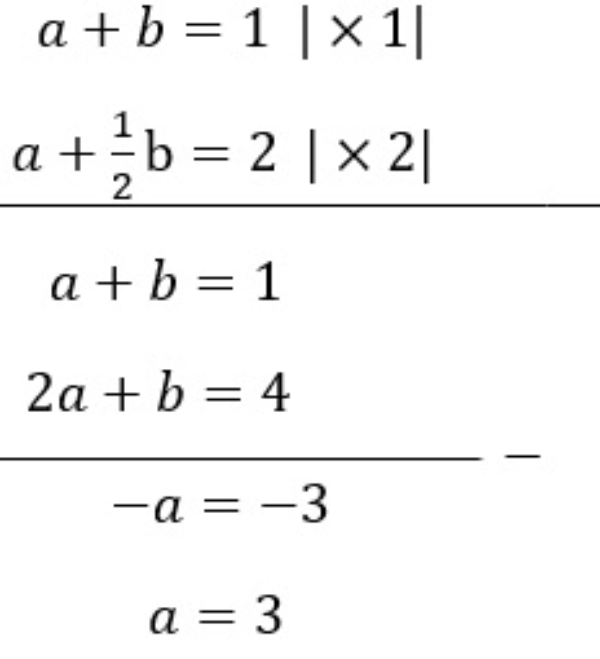Bank Soal Matematika SMA Nilai Rasio Trigonometri Sudut-Sudut Istimewa
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan tabel di bawah ini!
Tabel hasil penelitian "Pengaruh Cahaya Matahari Terhadap Warna Daun Tanaman Puring."
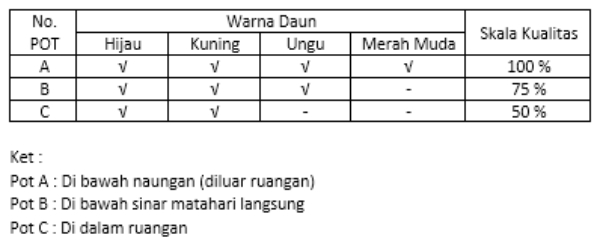
Berdasarkan informasi dari tabel di atas, jenis data dalam penelitian ini adalah ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Kerja Ilmiah dan Metode Ilmiah
Choose the correct answer.
Roy ... in Bandung for a few months.
Bahasa Inggris
Level 10
Congratulating and Complimenting
Tenses: Simple Present & Present Continuous
Setelah melakukan percobaan mengenai ayunan sederhana, data berupa panjang tali, massa bandul, jumlah getaran, dan waktu dihitung menggunakan rumus. Selanjutnya hasil perhitungan akan dibandingkan dengan teori apakah hasilnya sesuai atau tidak. Proses ini merupakan metode ilmiah tahap ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Hakikat dan Peran Fisika
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tingkat Keanekaragaman Hayati
Hasil dari adalah ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Konsep Nilai Mutlak
Sebelum menjadi makanan umum, bahan utama sate lilit adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Interpretasi dan Analisis Teks Laporan Hasil Observasi
Pada jaring-jaring makanan di bawah ini, organisme X berperan sebagai ....
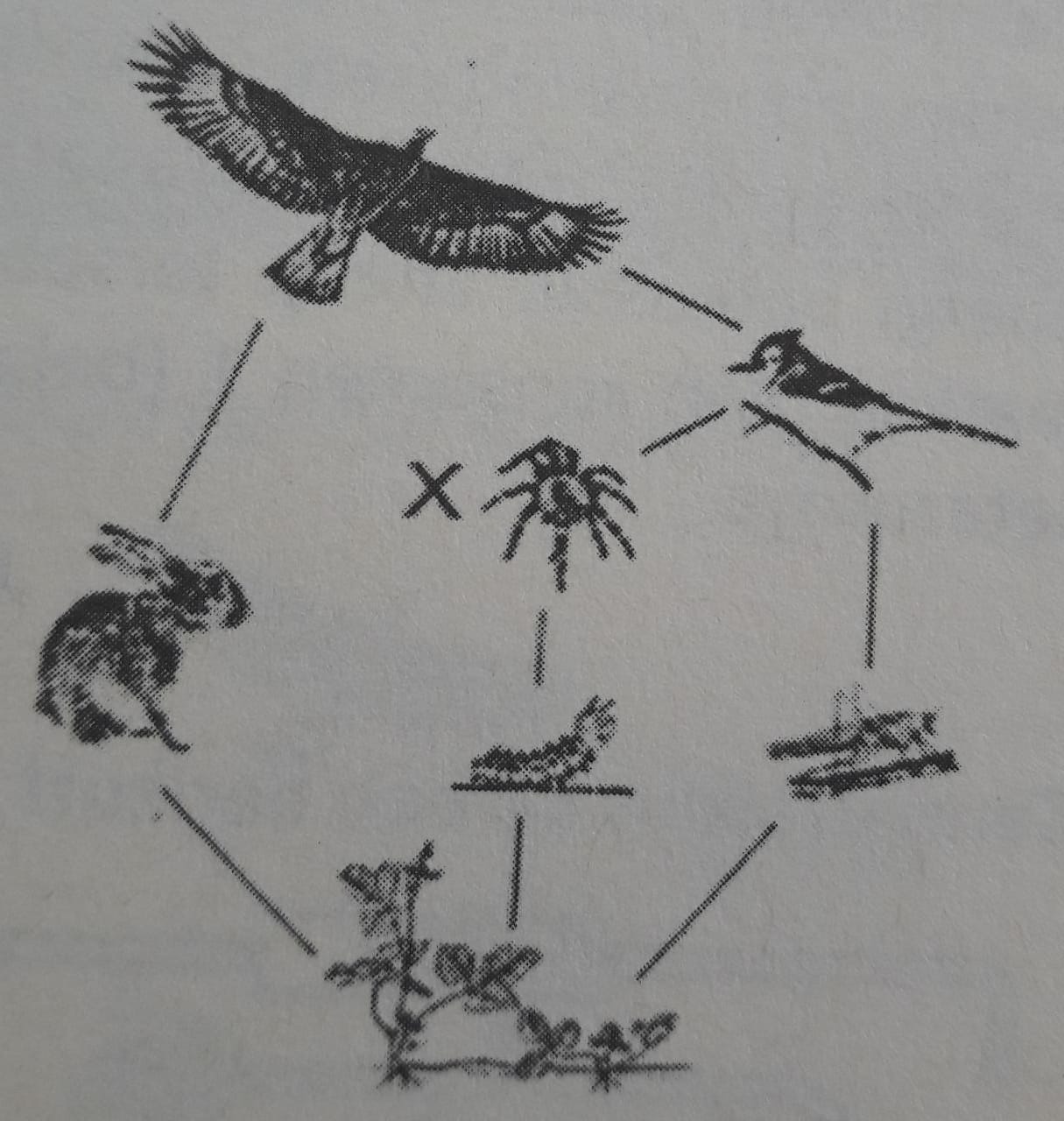
(UN 2014)
Biologi
Level 10
Biologi
Ekologi
Aliran Energi dan Piramida Ekologi
Perhatikan gambar berikut!
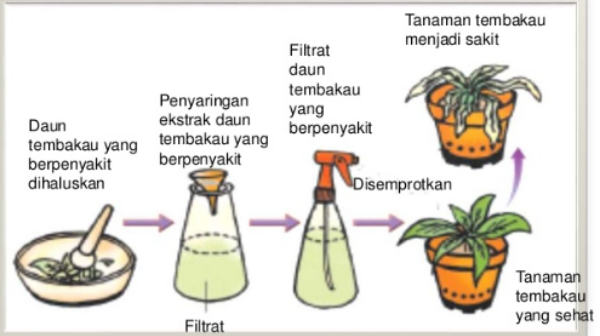
sumber: sucsload.blogspot.com
Penelitian pada tembakau seperti gambar di atas dilakukan oleh ....
Biologi
Level 10
Biologi
Virus
Sejarah Virus
Suatu campuran dapat dipisahkan zat-zat penyusunnya secara fisis. Contoh yang tepat untuk pemisahan secara fisis, kecuali ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Materi dan Klasifikasinya
Diketahui
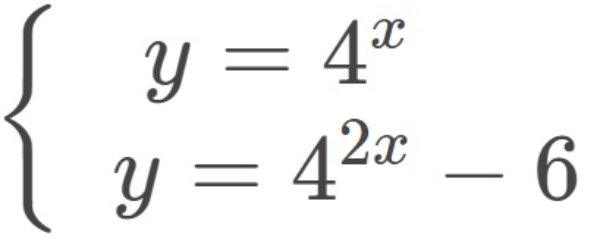
Himpunan penyelesaian untuk sistem persamaan dua variabel di atas adalah ....
Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Sistem Persamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan tabel di bawah ini!
Tabel hasil penelitian "Pengaruh Cahaya Matahari Terhadap Warna Daun Tanaman Puring."
Berdasarkan informasi dari tabel di atas, jenis data dalam penelitian ini adalah ....
Choose the correct answer.
Roy ... in Bandung for a few months.
Setelah melakukan percobaan mengenai ayunan sederhana, data berupa panjang tali, massa bandul, jumlah getaran, dan waktu dihitung menggunakan rumus. Selanjutnya hasil perhitungan akan dibandingkan dengan teori apakah hasilnya sesuai atau tidak. Proses ini merupakan metode ilmiah tahap ....
Perbedaan warna kulit manusia merupakan keanekaragaman pada tingkat ....
Hasil dari adalah ....
Sebelum menjadi makanan umum, bahan utama sate lilit adalah ….
Pada jaring-jaring makanan di bawah ini, organisme X berperan sebagai ....

(UN 2014)
Perhatikan gambar berikut!
sumber: sucsload.blogspot.com
Penelitian pada tembakau seperti gambar di atas dilakukan oleh ....
Suatu campuran dapat dipisahkan zat-zat penyusunnya secara fisis. Contoh yang tepat untuk pemisahan secara fisis, kecuali ....
Diketahui
Himpunan penyelesaian untuk sistem persamaan dua variabel di atas adalah ....