Bank Soal Matematika SMA Persamaan Garis Singgung Lingkaran
Soal
KurMer Kelas XI Matematika Lingkaran Skor 2
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
The underlined expression expresses ....
Bahasa Inggris
Level 11
Good Advice
Giving Advice or Suggestions
Kelas XI
Kurikulum 2013
K13
Bahasa Inggris
Perhatikan grafik berikut.
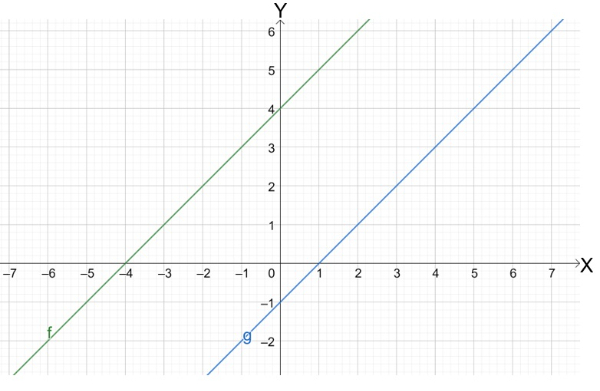
Translasi yang dapat memindahkan garis ke adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
Kelas XI
Kurikulum 2013
K13
Matematika Wajib
Di bawah ini penyakit yang disebabkan oleh kelainan lisosom, kecuali ....
Biologi
Level 11
Biologi
Sel
Struktur dan Fungsi Sel
Kelas XI
Kurikulum 2013
K13
Berikut ini yang merupakan contoh yang serupa dengan konsep induksi matematika adalah ....
Matematika
Level 11
Logika
Induksi Matematika
Konsep dan Prinsip Induksi Matematika
Kelas XI
Kurikulum 2013
K13
Matematika Wajib
Di bawah ini molekul yang paling mudah memasuki sel adalah ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Kelas XI
Kurikulum 2013
K13
Terdapat sebuah persamaan trigonometri , maka salah satu nilai dari dapat didefinisikan sebagai ....
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Kelas XI
Kurikulum 2013
K13
Matematika Peminatan
Perhatikan gambar berikut!
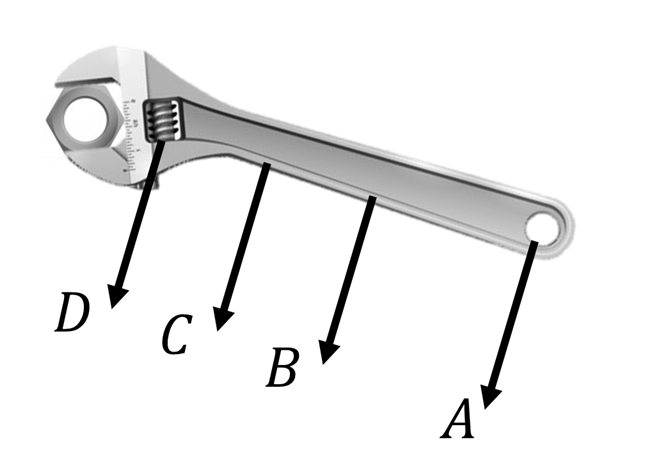
Jika kamu ingin melakukan putaran dengan gaya sekecil mungkin, maka kamu harus memutar kunci pada posisi ....
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Dinamika Benda Tegar
Kelas XI
Kurikulum 2013
K13

Choose the correct word or phrases to fill in the blank.
Bahasa Inggris
Level 11
Cause and Effect
Conjunctions, Transitions, and Prepositions
Kelas XI
Kurikulum 2013
K13
Bahasa Inggris
Jika merupakan titik singgung lingkaran maka persamaan garis singgungnya adalah ....
Matematika
Level 11,11
Geometri
Lingkaran
Persamaan Garis Singgung Lingkaran
Kelas XI
Kurikulum 2013
K13
Matematika Peminatan
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
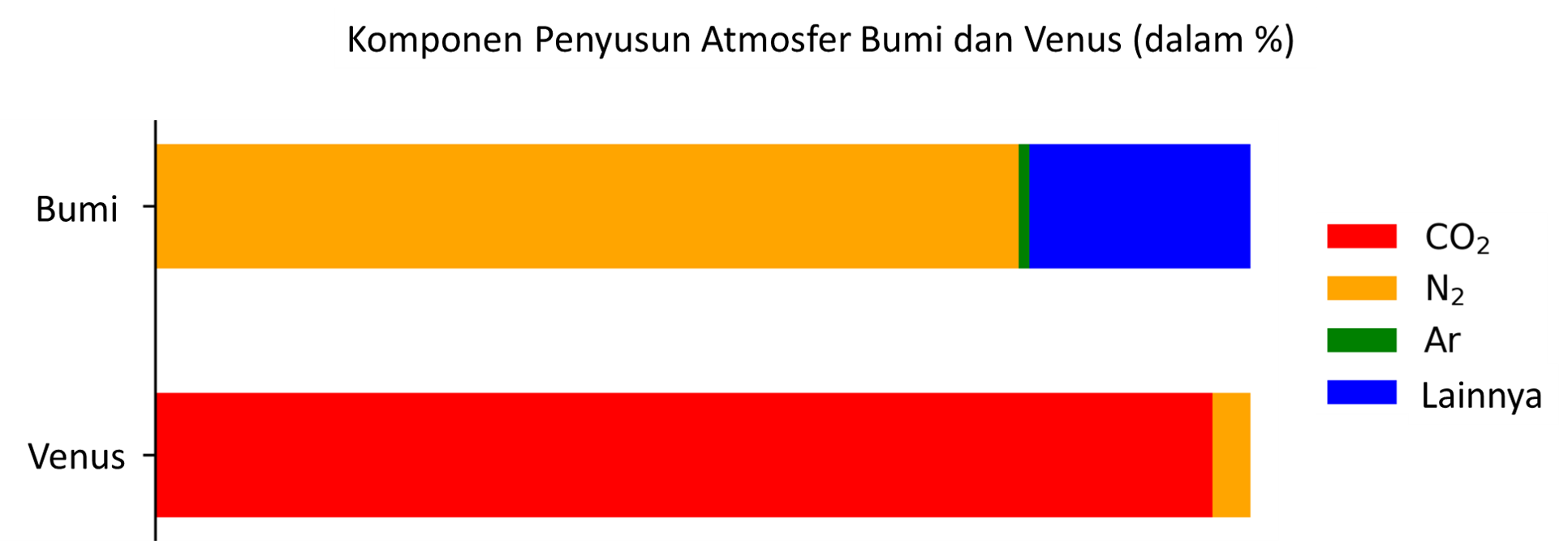
Pernyataan yang benar dari data tersebut dan fakta bahwa jarak Venus lebih dekat ke matahari dibanding Bumi adalah ....
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Kelas XI
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
The underlined expression expresses ....
Perhatikan grafik berikut.
Translasi yang dapat memindahkan garis ke adalah ....
Di bawah ini penyakit yang disebabkan oleh kelainan lisosom, kecuali ....
Berikut ini yang merupakan contoh yang serupa dengan konsep induksi matematika adalah ....
Di bawah ini molekul yang paling mudah memasuki sel adalah ....
Terdapat sebuah persamaan trigonometri , maka salah satu nilai dari dapat didefinisikan sebagai ....
Perhatikan gambar berikut!
Jika kamu ingin melakukan putaran dengan gaya sekecil mungkin, maka kamu harus memutar kunci pada posisi ....
Choose the correct word or phrases to fill in the blank.
Jika merupakan titik singgung lingkaran maka persamaan garis singgungnya adalah ....
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
Pernyataan yang benar dari data tersebut dan fakta bahwa jarak Venus lebih dekat ke matahari dibanding Bumi adalah ....



