Bank Soal Matematika SMA Jumlah, Selisih, dan Perkalian Sinus dan Cosinus
Soal
Matematika Peminatan LOTS
Video
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Objek dan Permasalahan Biologi
Kelas X
Kurikulum 2013
K13
Choose the correct answer.
Roy ... in Bandung for a few months.
Bahasa Inggris
Level 10
Congratulating and Complimenting
Tenses: Simple Present & Present Continuous
Kelas X
Kurikulum 2013
K13
Bahasa Inggris
Berikut penulisan nama spesies yang benar menurut tata nama binomial adalah ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Klasifikasi Makhluk Hidup
Kelas X
Kurikulum 2013
K13

Sumber: https://www.freepik.com/
Pada sebuah kegiatan eksperimen, seorang siswa mencampurkan metanol yang dia ambil dari kemasan berlabel seperti pada gambar. Bahan tersebut akan digunakan sebagai antibeku di dalam eksperimennya. Tetapi, pada saat mengambil bahan tersebut dia menghirupnya karena penasaran dan tiba-tiba mengalami penurunan kesadaran. Salah satu langkah yang tepat sebagai upaya pertolongan pertama pada kecelakaan tersebut adalah ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Keselamatan Kerja di Laboratorium
Kelas X
Kurikulum 2013
K13
Yang sesuai dengan sifat nilai mutlak yaitu ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Konsep Nilai Mutlak
Kelas X
Kurikulum 2013
K13
Matematika Wajib
Gagasan pokok paragraf kedua adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Interpretasi dan Analisis Teks Laporan Hasil Observasi
Kelas X
Kurikulum 2013
K13
Bahasa Indonesia
Dalam mekanisme suksesi terdapat sub-komponen eksesis. Pada proses ini terjadi proses ....
Biologi
Level 10
Biologi
Ekologi
Dinamika Komunitas
Kelas X
Kurikulum 2013
K13
Perhatikan gambar berikut!
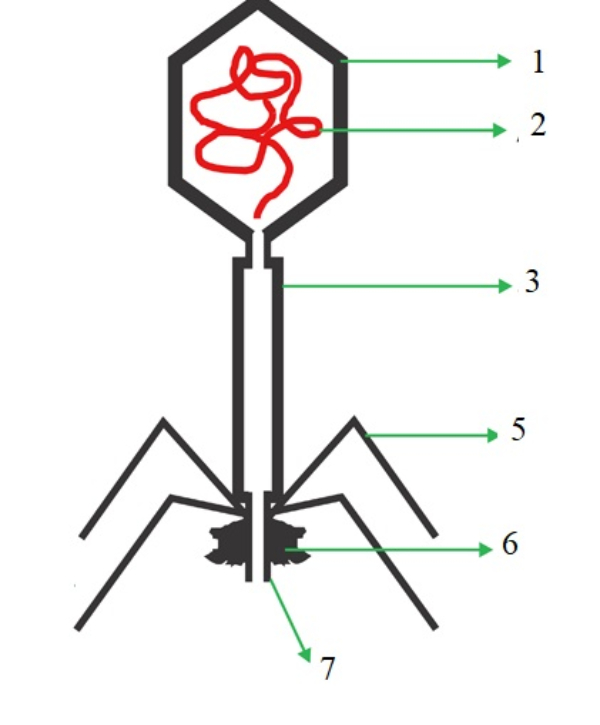
sumber: siswapedia.com
Dari gambar di atas, bagian nomor 1 sampai 7 secara berurutan adalah ....
Biologi
Level 10
Biologi
Virus
Ciri-Ciri Virus
Kelas X
Kurikulum 2013
K13
Himpunan penyelesaian dari persamaan adalah ....
Matematika
Level 10
Aljabar
Fungsi, Persamaan, dan Pertidaksamaan Eksponensial
Persamaan Eksponensial
Kelas X
Kurikulum 2013
K13
Matematika Peminatan
Dalam melaksanakan metode ilmiah, terkadang kesimpulan yang didapatkan tidaklah sesuai dengan hipotesis awal yang telah dibuat. Untuk itu, hal yang harus dilakukan adalah ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Metode Ilmiah dan Laboratorium Kimia
Kelas X
Kurikulum 2013
K13
Kimia
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
Choose the correct answer.
Roy ... in Bandung for a few months.
Berikut penulisan nama spesies yang benar menurut tata nama binomial adalah ....
Sumber: https://www.freepik.com/
Pada sebuah kegiatan eksperimen, seorang siswa mencampurkan metanol yang dia ambil dari kemasan berlabel seperti pada gambar. Bahan tersebut akan digunakan sebagai antibeku di dalam eksperimennya. Tetapi, pada saat mengambil bahan tersebut dia menghirupnya karena penasaran dan tiba-tiba mengalami penurunan kesadaran. Salah satu langkah yang tepat sebagai upaya pertolongan pertama pada kecelakaan tersebut adalah ....
Yang sesuai dengan sifat nilai mutlak yaitu ....
Gagasan pokok paragraf kedua adalah ….
Dalam mekanisme suksesi terdapat sub-komponen eksesis. Pada proses ini terjadi proses ....
Perhatikan gambar berikut!
sumber: siswapedia.com
Dari gambar di atas, bagian nomor 1 sampai 7 secara berurutan adalah ....
Himpunan penyelesaian dari persamaan adalah ....
Dalam melaksanakan metode ilmiah, terkadang kesimpulan yang didapatkan tidaklah sesuai dengan hipotesis awal yang telah dibuat. Untuk itu, hal yang harus dilakukan adalah ....



