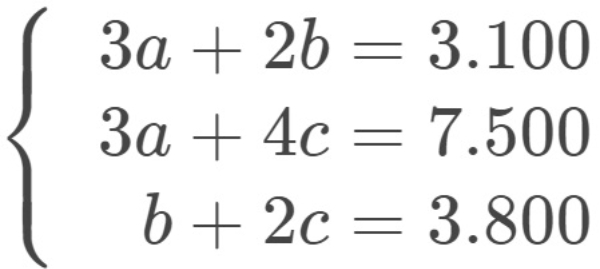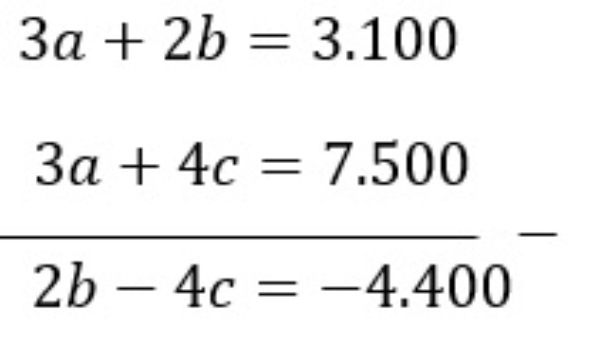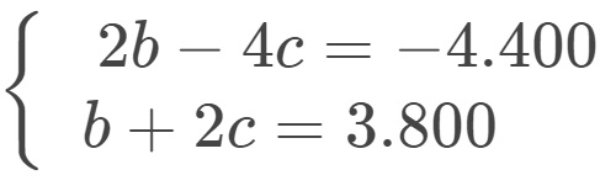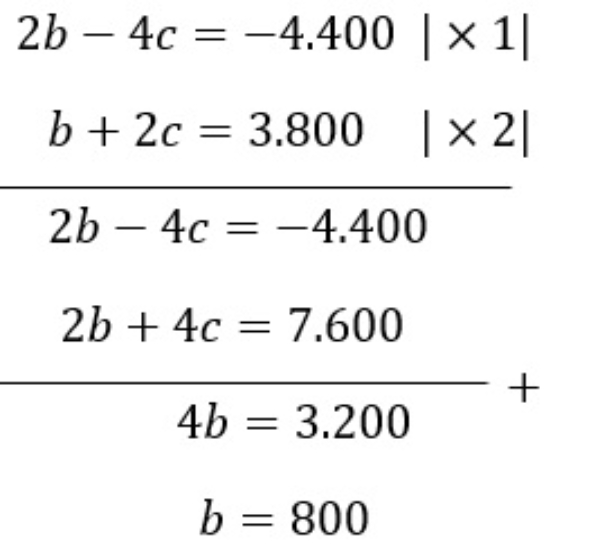Bank Soal Matematika SMA Sistem Persamaan Linear Tiga Variabel
Soal
Pemahaman Menghitung Level 5 Matematika Wajib LOTS Soal Cerita
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Pernyataan berikut yang merupakan pertidaksamaan linear satu variabel adalah ...
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Kalimat Benar, Salah, dan Terbuka
(i) (-50)2 -32 + 23 = 0
(ii) -82 : (22)3 = 20
(iii) 73 - 35 = 102
Pernyataan yang tepat adalah ...
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
Pak Arif, Pak Bagus, dan Pak Chiko adalah penduduk Desa Bahagia yang pekerjaannya bertani. Pak Arif menanam singkong, padi, dan kentang; Pak Bagus menanam talas, kentang, dan jagung; Pak Chiko menanam singkong dan kentang. Himpunan semua jenis tanaman penduduk Desa Bahagia yang bertani adalah …
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Ukuran keempat sudut yang dimiliki oleh persegi adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Konsep Sudut dan Garis
Teks yang menggambarkan keadaan, bentuk atau suasana tertentu adalah ....
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Ciri dan Tujuan Teks Deskripsi
Cermatilah penulisan alamat surat berikut ini.

Kesalahan penulisan bagian surat di atas adalah ...
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Unsur-unsur dan Kebahasaan Surat
Koefisien pada bentuk aljabar adalah ....
Matematika
Level 7
Aljabar
Bentuk Aljabar
Konsep Bentuk Aljabar
Perhatikan biografi berikut!

(Sumber gambar: akurat.co)
Salah satu penyanyi Indonesia yang pernah berduet dengan banyak penyanyi kenamaan Indonesia adalah Iwan Fals. Beliau pernah membawakan lagu berjudul Percayalah Kasih bersama Jockie Surjoprajogo dan Vina Panduwinata. Penyanyi dengan nama asli Virgiawan Lisanto ini merupakan salah satu legenda di Indonesia. Gaya musik yang dibawakannya adalah pop, rock, country, hingga folk pop. Lirik dari lagu-lagu Iwan Fals banyak menceritakan masa-masa kelam era 1970 hingga 1980-an di bidang politik. Salah satu lagunya bersama Swarmi yang berjudul Bongkar menerima penghargaan 150 lagu terbaik sepanjang masa versi Majalah Rolling Stone peringkat 1.
(Dikutip dari berbagai sumber)
Di bawah ini merupakan gaya musik yang dibawakan oleh Iwan Fals, kecuali ….
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Unsur Pembangun Buku Fiksi dan Nonfiksi
Kegiatan di bawah ini merupakan proses yang dilakukan dalam statistika, kecuali ....
Matematika
Level 7
Statistika
Penyajian dan Pengolahan Data
Penyajian dan Pengolahan Data
Read the text below and answer the question.

picture: freepik.com
My name is Kirana. I am an artist. I draw everyday. I work in my gallery at Jalan Laksa Adisucipto, Yogyakarta. I usually draw scenery and famous people.
What does Kirana do? She is ....
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Self Introduction
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pernyataan berikut yang merupakan pertidaksamaan linear satu variabel adalah ...
(i) (-50)2 -32 + 23 = 0
(ii) -82 : (22)3 = 20
(iii) 73 - 35 = 102
Pernyataan yang tepat adalah ...
Pak Arif, Pak Bagus, dan Pak Chiko adalah penduduk Desa Bahagia yang pekerjaannya bertani. Pak Arif menanam singkong, padi, dan kentang; Pak Bagus menanam talas, kentang, dan jagung; Pak Chiko menanam singkong dan kentang. Himpunan semua jenis tanaman penduduk Desa Bahagia yang bertani adalah …
Ukuran keempat sudut yang dimiliki oleh persegi adalah ....
Teks yang menggambarkan keadaan, bentuk atau suasana tertentu adalah ....
Cermatilah penulisan alamat surat berikut ini.
Kesalahan penulisan bagian surat di atas adalah ...
Koefisien pada bentuk aljabar adalah ....
Perhatikan biografi berikut!
(Sumber gambar: akurat.co)
Salah satu penyanyi Indonesia yang pernah berduet dengan banyak penyanyi kenamaan Indonesia adalah Iwan Fals. Beliau pernah membawakan lagu berjudul Percayalah Kasih bersama Jockie Surjoprajogo dan Vina Panduwinata. Penyanyi dengan nama asli Virgiawan Lisanto ini merupakan salah satu legenda di Indonesia. Gaya musik yang dibawakannya adalah pop, rock, country, hingga folk pop. Lirik dari lagu-lagu Iwan Fals banyak menceritakan masa-masa kelam era 1970 hingga 1980-an di bidang politik. Salah satu lagunya bersama Swarmi yang berjudul Bongkar menerima penghargaan 150 lagu terbaik sepanjang masa versi Majalah Rolling Stone peringkat 1.
(Dikutip dari berbagai sumber)
Di bawah ini merupakan gaya musik yang dibawakan oleh Iwan Fals, kecuali ….
Kegiatan di bawah ini merupakan proses yang dilakukan dalam statistika, kecuali ....
Read the text below and answer the question.
picture: freepik.com
My name is Kirana. I am an artist. I draw everyday. I work in my gallery at Jalan Laksa Adisucipto, Yogyakarta. I usually draw scenery and famous people.
What does Kirana do? She is ....