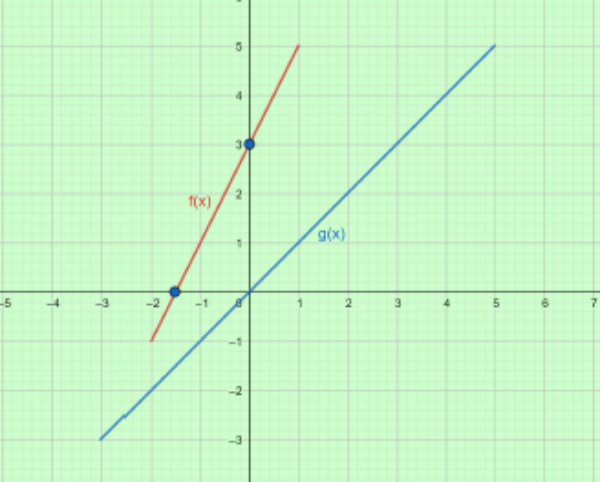
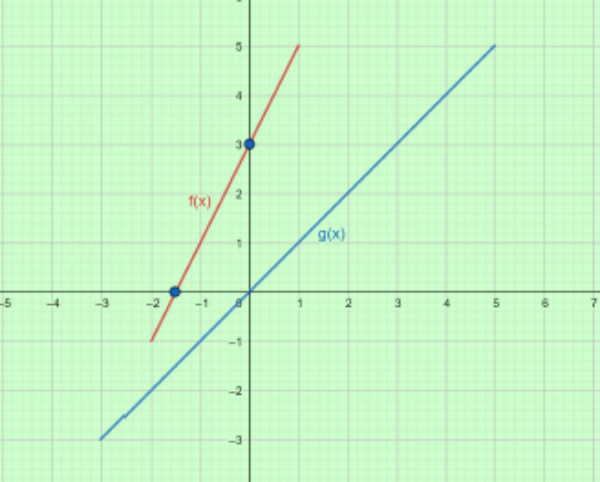
Bank Soal Matematika SMA Operasi Komposisi pada Fungsi
Soal
Pilgan
Pembahasan
Rangkuman

08 April 2020
Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya
Lihat Semua Rangkuman dan Materi



Soal Populer Hari Ini
8.250 dibaca ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Membilang Sampai 10.000
Perhatikan gambar berikut.

Kalimat yang sesuai dengan gambar adalah …
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menulis Kalimat Sesuai Gambar
Perhatikan data usia siswa kelas III pada diagram di bawah ini!
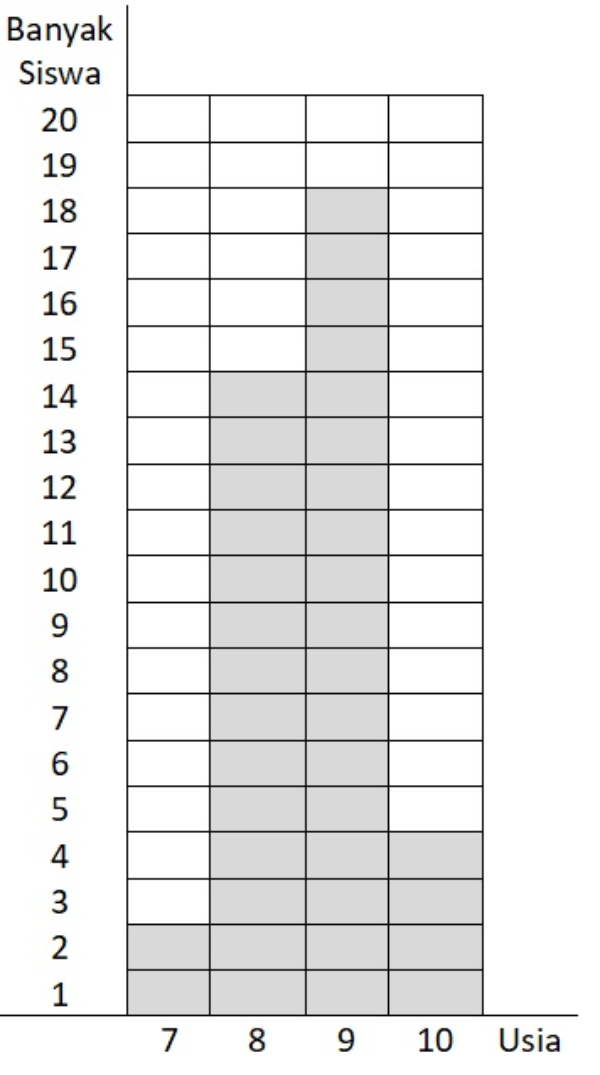
Berapa siswa yang mempunyai usia tertinggi?
Matematika
Level 3
Statistika
Data
Membaca dan Menafsirkan Data
Perhatikan denah berikut!
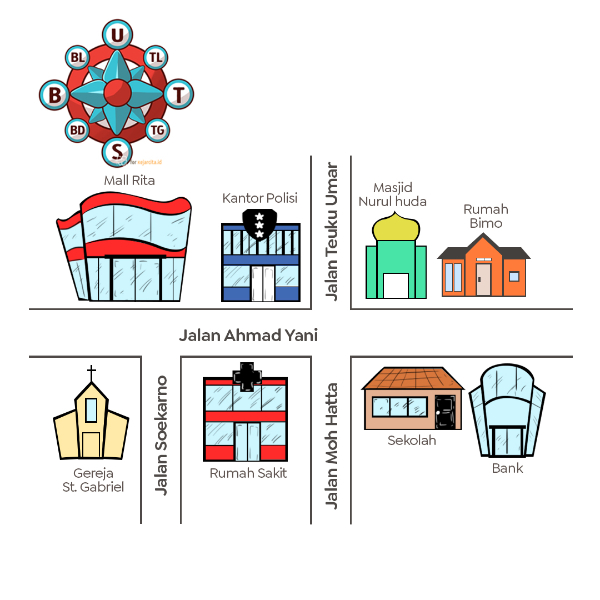
Kantor polisi berada di sebelah ... rumah sakit.
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
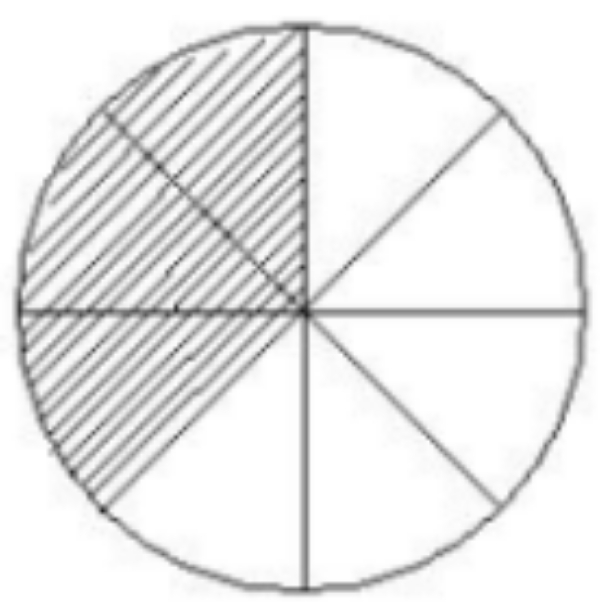
Bagian yang tidak diarsir pada gambar di atas menunjukkan pecahan ...
Matematika
Level 3
Bilangan
Pecahan Sederhana
Menentukan Nilai Pecahan
1 kg 275 gram = ... gram
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Hubungan Antarsatuan Berat
Mutia mengisi botol air dengan gelas hingga penuh.
Berikut adalah gambaran botol air yang diisi Mutia hingga penuh dengan gelas.
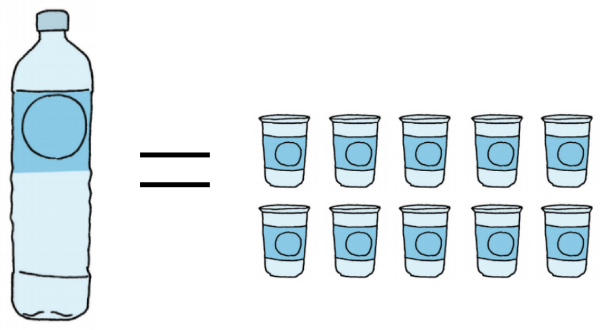
(Sumber Gambar: Buku BSE Kelas 3)
Arti dari gambaran di atas adalah ...
Matematika
Level 3
Geometri
Volume Bangun Ruang
Konsep Volume
Perhatikan ciri-ciri bangun datar berikut!
- Memiliki dua pasang sisi yang sama panjang
- Mempunyai dua diagonal yang tidak sama panjang
- Memiliki sepasang sudut yang sama besar
- Mempunyai 1 simetri putar
- Mempunyai 1 simetri lipat
Bangun datar yang dimaksud adalah ....
Matematika
Level 3
Geometri
Bangun Datar
Unsur dan Sifat Bangun Datar

Sifat distributif yang benar berada pada kolom ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Sifat-Sifat Operasi Hitung Bilangan Cacah
Menentukan narasumber dilakukan [...] wawancara.
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menggali Informasi melalui Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
8.250 dibaca ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Membilang Sampai 10.000
Perhatikan gambar berikut.
Kalimat yang sesuai dengan gambar adalah …
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menulis Kalimat Sesuai Gambar
Perhatikan data usia siswa kelas III pada diagram di bawah ini!
Berapa siswa yang mempunyai usia tertinggi?
Matematika
Level 3
Statistika
Data
Membaca dan Menafsirkan Data
Perhatikan denah berikut!
Kantor polisi berada di sebelah ... rumah sakit.
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
Bagian yang tidak diarsir pada gambar di atas menunjukkan pecahan ...
Matematika
Level 3
Bilangan
Pecahan Sederhana
Menentukan Nilai Pecahan
1 kg 275 gram = ... gram
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Hubungan Antarsatuan Berat
Mutia mengisi botol air dengan gelas hingga penuh.
Berikut adalah gambaran botol air yang diisi Mutia hingga penuh dengan gelas.
(Sumber Gambar: Buku BSE Kelas 3)
Arti dari gambaran di atas adalah ...
Matematika
Level 3
Geometri
Volume Bangun Ruang
Konsep Volume
Perhatikan ciri-ciri bangun datar berikut!
- Memiliki dua pasang sisi yang sama panjang
- Mempunyai dua diagonal yang tidak sama panjang
- Memiliki sepasang sudut yang sama besar
- Mempunyai 1 simetri putar
- Mempunyai 1 simetri lipat
Bangun datar yang dimaksud adalah ....
Matematika
Level 3
Geometri
Bangun Datar
Unsur dan Sifat Bangun Datar
Sifat distributif yang benar berada pada kolom ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Sifat-Sifat Operasi Hitung Bilangan Cacah
Menentukan narasumber dilakukan [...] wawancara.
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menggali Informasi melalui Wawancara