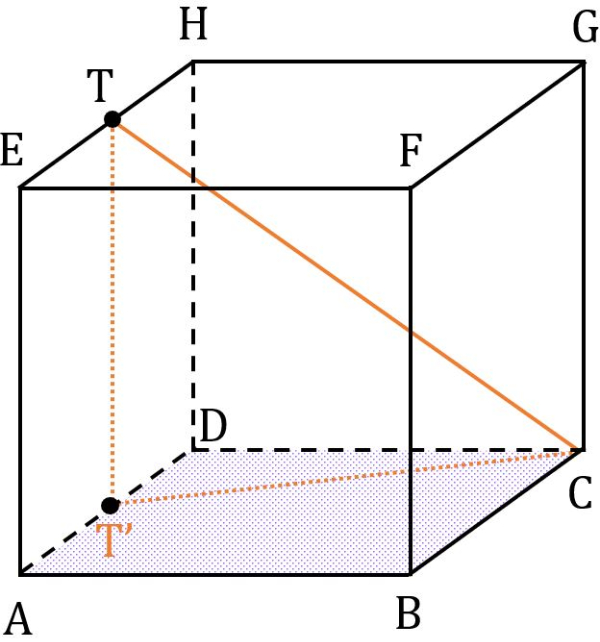
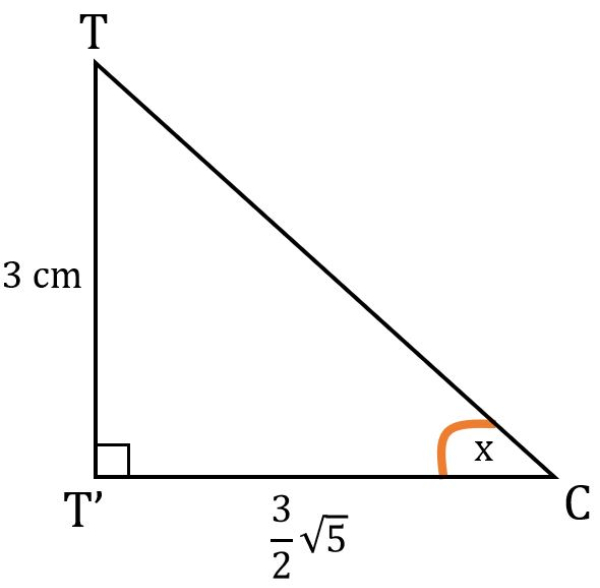
Bank Soal Matematika SMA Sudut pada Bangun Ruang
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Read the text below.
Cheese and Mushroom Toast
1 – 2 mins
Ingredients:
- 3 slices white bread (sandwich loaf)
- 100 g mushrooms in oil, finely chopped
- 20 g cheese, grated
Methods:
- After cutting the crusts off the bread, spread the finely chopped mushrooms over each slice.
- Sprinkle with grated cheese and cut each slice into four.
- Lay the pieces in a microwaveable dish and cook at 750 W for 1-2 minutes.
- Your meal is ready to serve.
source: Cook Book by Whirlpool
'Lay the pieces in a microwaveable dish and cook at 750 W for 1-2 minutes.' (last step).
The word lay in the sentence above can be replaced with ....
Bahasa Inggris
Level 9
Bahasa Inggris
How to do or make things
Procedure Text
Observe the classroom reward chart below and answer the question.

Source: canva.com
Which of the following information is NOT stated on the chart?
Bahasa Inggris
Level 9
Bahasa Inggris
Using passive voice to describe things
Passive Voice
Permasalahan berikut yang dapat dikembangkan untuk menjadi sebuah teks laporan percobaan adalah ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Identifikasi Laporan Percobaan
Nilai dari perpangkatan adalah...
Matematika
Level 9
Bilangan
Bilangan Berpangkat dan Bentuk Akar
Bilangan Berpangkat
Baca teks berikut ini dengan cermat.
Pro dan Kontra Warga Jakarta Menyikapi Penerapan Tilang ETLE
Penerbitan aturan berkendara di jalan belum begitu efektif membuat para pengendara motor patuh. Meskipun sudah ada personel polisi yang bertugas menertibkan lalu lintas, masih banyak pengendara yang bandel. Berangkat dari permasalahan tersebut, Kepolisian Daerah Metropolitan Jakarta Raya (Polda Metro Jaya) menerapkan sistem tilang elektronik atau ETLE (electronic traffic law enforcement). ETLE rencananya mulai diperluas pada Februari 2020.
Tilang elektronik akan diterapkan di beberapa titik di Jakarta dan Bekasi. Penerapan tilang tersebut dilakukan dengan memasang kamera-kamera di beberapa bahu jalan untuk merekam pelanggaran yang dilakukan oleh pengendara motor. Foto dan video dari kamera ETLE nantinya akan diverifikasi oleh petugas dan akan dikirim ke rumah pengendara yang melanggar.
Meskipun program ETLE bertujuan baik, masih ada masyarakat yang kurang setuju. Jaenal, seorang pengemudi ojek online asal Kebon Jeruk, kurang setuju dengan adanya tilang format baru tersebut. Jaenal merasa tilang ETLE akan merugikannya ketika mencari dan mendapatkan penumpang. "Saya kurang setuju dengan tilang eletronik. Kalau kebetulan saya lewat Bundaran Senayan Ratu Plaza (Salah satu titik kamera ETLE) sambil megang handphone karena menghubungi penumpang bagaimana?" ujar Jaenal.
Di sisi lain, banyak pihak yang sepakat dengan penerapan tilang ETLE. Johan, pemuda asal Pondok Gede justru lebih menyukai sistem tilang ETLE. "Iya, kalau tilang yang ketemu polisi langsung kan suka ada transaksi ilegal, jadi kurang adil," ujar Johan. Ada juga Abidin yang berpendapat kalau tilang ETLE lebih efektif daripada tilang Ditlantas turun ke jalan. "Kalau yang ditangkap kamera kan lebih jelas pelanggarannya apa. Kalau yang tilang langsung di jalan kadang suka cari-cari kesalahan, kadang harus mengeluarkan uang lebih," ujar Abidin.
Karena persoalannya adalah lalu lintas jalanan umum, maka yang harus diutamakan adalah kebaikan pengendara. Tilang ETLE hadir untuk meningkatkan ketertiban sekaligus keselamatan di jalan. Oleh karena itu bagi pengendara yang melakukan aktivitas lain ketika di jalan, sebaiknya berhenti atau minggir terlebih dahulu. Masyarakat dan polisi diharapkan saling bekerja sama menjaga ketertiban dan keselamatan dalam berlalu lintas.
(Sumber: Kompas.com, dengan penyesuaian)
Alasan diadakannya sistem tilang elektronik atau ETLE adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Menggali Informasi Teks Diskusi
Berikut yang merupakan bagian pembahasan laporan percobaan adalah ...
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Struktur dan Kebahasaan Laporan Percobaan
Read the following text and answer the question.

Source: classof2020.ucsc.edu
The following statements are right about the message, except ...
Bahasa Inggris
Level 9
Bahasa Inggris
Appreciation over achievements or happiness
Expressions of Congratulations
Baca teks berikut dengan cermat.
Melisa, Siswa SD Berprestasi Meski Menulis Hanya Menggunakan Kaki
Melisa Diana Putri adalah seorang siswi difabel di SDN Tukul II Kecamatan Sumber, Kabupaten Probolinggo, Jawa Timur. Melisa duduk di kelas 8. Ia bercita-cita menjadi guru. Semangatnya sangat tinggi meski ia belajar dan beraktivitas menggunakan kaki.
Melisa mengikuti pelajaran di sekolah bersama teman-temannya seperti biasa. Namun saat menulis di buku tulis, dia menggunakan jari kaki. Oleh sekolah, meja khusus dia menulis dibuat lebih rendah dari tubuhnya. Saat menulis di papan tulis untuk mengerjakan tugas dari guru, ia juga menggunakan kaki. Kaki kirinya menopang tubuh agar seimbang, sementara kaki kanannya lincah menulis di papan tulis. Meski menggunakan kaki sejak lahir, tulisan Melisa rapi.
Meskipun memiliki keterbatasan fisik, Melisa sangat tekun dalam belajar. Ia sangat bersemangat meraih prestasi dan nilai baik. Menurut pengakuan gurunya, Melisa memang sangat jago matematika. Selain itu, Melisa juga hobi membaca. Buku apa pun dia baca. Melisa mengaku, ia membaca buku untuk memperluas wawasan.
Menurut Tri Adi Nurfeni, guru Bahasa Indonesia, Melisa meraih cukup banyak prestasi. Melisa pernah juara lomba baca, tulis dan hitung tingkat kecamatan, dan ditunjuk menjadi duta sekolah karena pengetahuannya yang bagus. Berkat pencapaian Melisa, Wakil Bupati Timbul Prihanjoko mengunjungi Melisa di sekolah. Joko, panggilan akrab Wakil Bupati Probolinggi, terharu melihat semangat Melisa untuk meraih cita-cita. Joko dan sejumlah pejabat Pemkab Probolinggo memberi sejumlah bantuan untuk kelanjutan belajar Melisa.
Melisa menjadi bukti bahwa keterbatasan fisik tidak menghalangi seseorang dalam meraih prestasi. Berkat ketekunan dalam belajar, Melisa dapat menghilangkan keterbatasan-keterbatasan itu tadi.
(Sumber: Kompas.com, dengan penyesuaian)
Simpulan yang tepat dari cerita inspiratif di atas adalah ...
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Perbedaan teks diskusi dengan teks eksposisi adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Menggali Informasi Teks Diskusi
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Tokoh utama dalam cerita di atas adalah ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Read the text below.
Cheese and Mushroom Toast
1 – 2 mins
Ingredients:
- 3 slices white bread (sandwich loaf)
- 100 g mushrooms in oil, finely chopped
- 20 g cheese, grated
Methods:
- After cutting the crusts off the bread, spread the finely chopped mushrooms over each slice.
- Sprinkle with grated cheese and cut each slice into four.
- Lay the pieces in a microwaveable dish and cook at 750 W for 1-2 minutes.
- Your meal is ready to serve.
source: Cook Book by Whirlpool
'Lay the pieces in a microwaveable dish and cook at 750 W for 1-2 minutes.' (last step).
The word lay in the sentence above can be replaced with ....
Observe the classroom reward chart below and answer the question.
Source: canva.com
Which of the following information is NOT stated on the chart?
Permasalahan berikut yang dapat dikembangkan untuk menjadi sebuah teks laporan percobaan adalah ....
Nilai dari perpangkatan adalah...
Baca teks berikut ini dengan cermat.
Pro dan Kontra Warga Jakarta Menyikapi Penerapan Tilang ETLE
Penerbitan aturan berkendara di jalan belum begitu efektif membuat para pengendara motor patuh. Meskipun sudah ada personel polisi yang bertugas menertibkan lalu lintas, masih banyak pengendara yang bandel. Berangkat dari permasalahan tersebut, Kepolisian Daerah Metropolitan Jakarta Raya (Polda Metro Jaya) menerapkan sistem tilang elektronik atau ETLE (electronic traffic law enforcement). ETLE rencananya mulai diperluas pada Februari 2020.
Tilang elektronik akan diterapkan di beberapa titik di Jakarta dan Bekasi. Penerapan tilang tersebut dilakukan dengan memasang kamera-kamera di beberapa bahu jalan untuk merekam pelanggaran yang dilakukan oleh pengendara motor. Foto dan video dari kamera ETLE nantinya akan diverifikasi oleh petugas dan akan dikirim ke rumah pengendara yang melanggar.
Meskipun program ETLE bertujuan baik, masih ada masyarakat yang kurang setuju. Jaenal, seorang pengemudi ojek online asal Kebon Jeruk, kurang setuju dengan adanya tilang format baru tersebut. Jaenal merasa tilang ETLE akan merugikannya ketika mencari dan mendapatkan penumpang. "Saya kurang setuju dengan tilang eletronik. Kalau kebetulan saya lewat Bundaran Senayan Ratu Plaza (Salah satu titik kamera ETLE) sambil megang handphone karena menghubungi penumpang bagaimana?" ujar Jaenal.
Di sisi lain, banyak pihak yang sepakat dengan penerapan tilang ETLE. Johan, pemuda asal Pondok Gede justru lebih menyukai sistem tilang ETLE. "Iya, kalau tilang yang ketemu polisi langsung kan suka ada transaksi ilegal, jadi kurang adil," ujar Johan. Ada juga Abidin yang berpendapat kalau tilang ETLE lebih efektif daripada tilang Ditlantas turun ke jalan. "Kalau yang ditangkap kamera kan lebih jelas pelanggarannya apa. Kalau yang tilang langsung di jalan kadang suka cari-cari kesalahan, kadang harus mengeluarkan uang lebih," ujar Abidin.
Karena persoalannya adalah lalu lintas jalanan umum, maka yang harus diutamakan adalah kebaikan pengendara. Tilang ETLE hadir untuk meningkatkan ketertiban sekaligus keselamatan di jalan. Oleh karena itu bagi pengendara yang melakukan aktivitas lain ketika di jalan, sebaiknya berhenti atau minggir terlebih dahulu. Masyarakat dan polisi diharapkan saling bekerja sama menjaga ketertiban dan keselamatan dalam berlalu lintas.
(Sumber: Kompas.com, dengan penyesuaian)
Alasan diadakannya sistem tilang elektronik atau ETLE adalah ....
Berikut yang merupakan bagian pembahasan laporan percobaan adalah ...
Read the following text and answer the question.
Source: classof2020.ucsc.edu
The following statements are right about the message, except ...
Baca teks berikut dengan cermat.
Melisa, Siswa SD Berprestasi Meski Menulis Hanya Menggunakan Kaki
Melisa Diana Putri adalah seorang siswi difabel di SDN Tukul II Kecamatan Sumber, Kabupaten Probolinggo, Jawa Timur. Melisa duduk di kelas 8. Ia bercita-cita menjadi guru. Semangatnya sangat tinggi meski ia belajar dan beraktivitas menggunakan kaki.
Melisa mengikuti pelajaran di sekolah bersama teman-temannya seperti biasa. Namun saat menulis di buku tulis, dia menggunakan jari kaki. Oleh sekolah, meja khusus dia menulis dibuat lebih rendah dari tubuhnya. Saat menulis di papan tulis untuk mengerjakan tugas dari guru, ia juga menggunakan kaki. Kaki kirinya menopang tubuh agar seimbang, sementara kaki kanannya lincah menulis di papan tulis. Meski menggunakan kaki sejak lahir, tulisan Melisa rapi.
Meskipun memiliki keterbatasan fisik, Melisa sangat tekun dalam belajar. Ia sangat bersemangat meraih prestasi dan nilai baik. Menurut pengakuan gurunya, Melisa memang sangat jago matematika. Selain itu, Melisa juga hobi membaca. Buku apa pun dia baca. Melisa mengaku, ia membaca buku untuk memperluas wawasan.
Menurut Tri Adi Nurfeni, guru Bahasa Indonesia, Melisa meraih cukup banyak prestasi. Melisa pernah juara lomba baca, tulis dan hitung tingkat kecamatan, dan ditunjuk menjadi duta sekolah karena pengetahuannya yang bagus. Berkat pencapaian Melisa, Wakil Bupati Timbul Prihanjoko mengunjungi Melisa di sekolah. Joko, panggilan akrab Wakil Bupati Probolinggi, terharu melihat semangat Melisa untuk meraih cita-cita. Joko dan sejumlah pejabat Pemkab Probolinggo memberi sejumlah bantuan untuk kelanjutan belajar Melisa.
Melisa menjadi bukti bahwa keterbatasan fisik tidak menghalangi seseorang dalam meraih prestasi. Berkat ketekunan dalam belajar, Melisa dapat menghilangkan keterbatasan-keterbatasan itu tadi.
(Sumber: Kompas.com, dengan penyesuaian)
Simpulan yang tepat dari cerita inspiratif di atas adalah ...
Perbedaan teks diskusi dengan teks eksposisi adalah ....
Baca teks berikut ini dengan cermat.
Bukan Uang, Sekolah Ini Minta Siswanya Bayar Pakai Sampah Plastik
Selama ini, plastik selalu dipandang sebagai masalah dan limbah yang mengotori lingkungan. Sebenarnya sampah juga mempunyai nilai guna apabila dilakukan daur ulang. Bahkan bagi sebagian orang sampah adalah barang yang berharga dan menjadi tumpuan hidup. Sebagaimana sebuah sekolah di India yang menggunakan sampah plastik sebagai pengganti uang sekolah yang harus dibayar oleh siswa.
Akshar Foundation adalah sekolah yang menerapkan program penerimaan limbah plastik untuk didaur ulang. Sekolah yang berada di Desa Pamohi, Guwahati, India tersebut didirikan oleh Parmita Sharma dan Mazin Mukthar. Program daur ulang limbah yang sekolah mereka terapkan juga mengajak siswa terlibat dalam pengumpulan dan pemisahan sampah.
Ketika awal membuka Akshar Foundation, Parmita dan Mizan mengalami kesulitan. Sebagian besar orangtua tidak mau memasukkan anak-anak mereka ke sekolah. Penyebabnya adalah karena mereka tidak punya biaya untuk membayar uang sekolah anaknya. Para orang tua memilih mengajak anaknya untuk bekerja di pertambangan. Namun Parmita dan Mizan tak patah semangat. Mereka mempunyai satu misi ingin memberikan pendidikan bagi anak-anak dari keluarga kurang mampu.
Parmita dan Mizan pun akhirnya memulai program sekolah gratis untuk semua anak. Lebih tepatnya bukan gratis, melainkan mengganti uang sekolah dengan sampah plastik. Akshar Foundation mewajibkan para siswanya untuk mengumpulkan dan membawa sampah plastik ke sekolah. Program tersebut berawal ketika mereka menyadari ada masalah sosial dan ekologi di lingkungan sekolah mereka.
Gerakan yang dilakukan Parmita dan Mazin mendapat apresiasi dari banyak pihak. Wakil Presiden Akshar, Priyongsu Borthakur, mengatakan bahwa ide mereka sangat mengesankan dan sangat berjasa. Dukungan dalam bentuk lain adalah menjadi banyak anak yang mendaftar di Akshar Foundation. Sekolah yang bermula dengan 20 siswa tersebut kini sudah memiliki hampir 100 siswa yang berusia antara 4 - 15 tahun.
(Sumber: Liputan6.com, dengan penyesuaian)
Tokoh utama dalam cerita di atas adalah ....