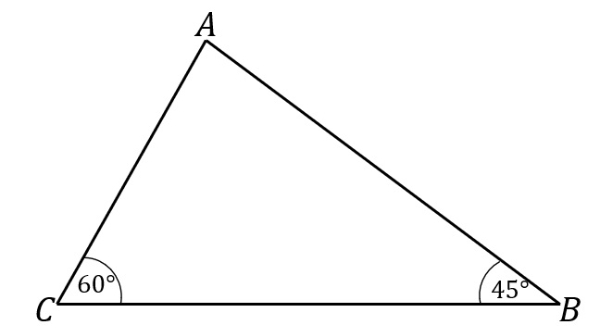
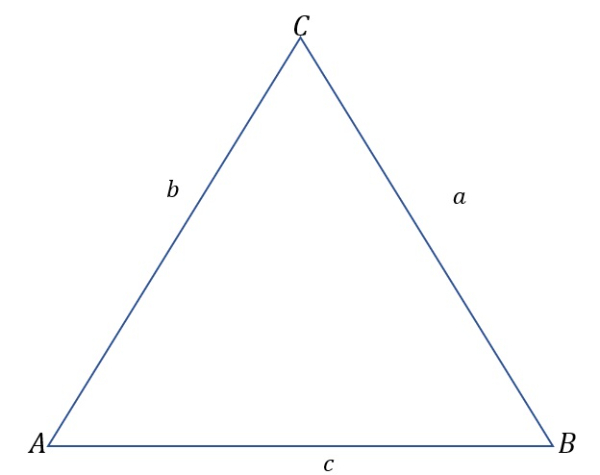
Bank Soal Matematika SMA Aturan Sinus
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan garis bilangan dibawah ini!
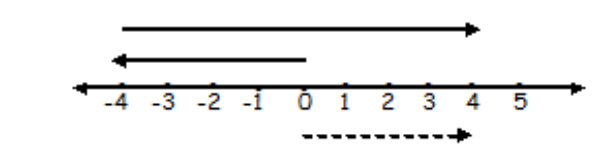
Kalimat matematika yang sesuai dengan gambar di atas adalah ...
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Complete the sentence using the verb. Use past tense.

Last holiday, me and my dad … (go) on a road trip to Bandung. We … (not / forget) to bring many food and drink. It was tiring, but fun!
Bahasa Inggris
Level 6
Bahasa Inggris
Past Holidays
Recount Text
Kata tanya yang digunakan untuk menanyakan alasan atau penyebab suatu peristiwa sejarah adalah ....
Bahasa Indonesia
Level 6
Membaca
Buku Sejarah
Menggali Informasi (5W+1H)
Sebuah prisma segitiga mempunyai sisi sebanyak ... buah.
Matematika
Level 6
Geometri
Bangun Ruang
Sifat dan Jaring-Jaring Bangun Ruang
Perhatikan gambar berikut!
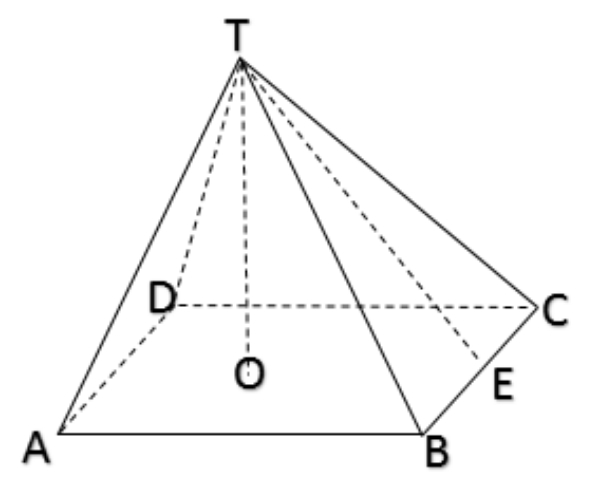
Jika AB = 16 cm, BC = 20 cm, TO = 6 cm, TE =10 cm, dan tinggi semua sisi tegak adalah sama, maka luas permukaan bangun limas di atas adalah ... cm2.
Matematika
Level 6
Geometri
Bangun Ruang
Volume dan Luas Permukaan Bangun Ruang
Hasil
Matematika
Level 6
Bilangan
Operasi Hitung Bilangan Bulat dan Pecahan
Operasi Hitung Bilangan Bulat
Bacalah paragraf berikut!
Pada tanggal 9-15 April 2019, siswa kelas VI SD Pelita Bangsa melakukan pengamatan terhadap Sungai Brantas. Debit airnya cukup. Namun, masih ditemukan sampah di sungai tersebut, yang disebabkan oleh masyarakat yang kurang menjaga kebersihan sungai. Mereka membuang sampah rumah tangga ke dalam sungai.
Kesimpulan paragraf laporan tersebut adalah ...
Bahasa Indonesia
Level 6
Menulis
Teks Laporan Hasil Pengamatan
Menyimpulkan Informasi
Pak Min mempunyai 3 kandang ayam. Setiap kandang berisi 40 ekor ayam dan 12 ekor diantaranya ayam jantan. Pada suatu hari, semua ayam betina bertelur masing-masing 1 butir. Jika telur-telur tersebut ditempatkan dalam 14 wadah secara merata. Setiap wadah memuat telur sebanyak ... butir
Perhatikan contoh perkembangbiakan secara vegatatif di bawah ini!
- Umbi lapis
- Umbi batang
- Cangkok
- Tunas adventif
- Merunduk
Perkembangbiakan secara vegetatif alami ditunjuk oleh nomor ....
IPA
Level 6
Biologi
Perkembangbiakan Makhluk Hidup
Perkembangbiakan Tumbuhan
Paragraf penutup yang sesuai untuk pidato kelulusan siswa yang disampaikan kepala sekolah adalah …
Bahasa Indonesia
Level 6
Membaca
Teks Pidato
Menulis Teks Pidato
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan garis bilangan dibawah ini!
Kalimat matematika yang sesuai dengan gambar di atas adalah ...
Complete the sentence using the verb. Use past tense.

Last holiday, me and my dad … (go) on a road trip to Bandung. We … (not / forget) to bring many food and drink. It was tiring, but fun!
Kata tanya yang digunakan untuk menanyakan alasan atau penyebab suatu peristiwa sejarah adalah ....
Sebuah prisma segitiga mempunyai sisi sebanyak ... buah.
Perhatikan gambar berikut!
Jika AB = 16 cm, BC = 20 cm, TO = 6 cm, TE =10 cm, dan tinggi semua sisi tegak adalah sama, maka luas permukaan bangun limas di atas adalah ... cm2.
Hasil
Bacalah paragraf berikut!
Pada tanggal 9-15 April 2019, siswa kelas VI SD Pelita Bangsa melakukan pengamatan terhadap Sungai Brantas. Debit airnya cukup. Namun, masih ditemukan sampah di sungai tersebut, yang disebabkan oleh masyarakat yang kurang menjaga kebersihan sungai. Mereka membuang sampah rumah tangga ke dalam sungai.
Kesimpulan paragraf laporan tersebut adalah ...
Pak Min mempunyai 3 kandang ayam. Setiap kandang berisi 40 ekor ayam dan 12 ekor diantaranya ayam jantan. Pada suatu hari, semua ayam betina bertelur masing-masing 1 butir. Jika telur-telur tersebut ditempatkan dalam 14 wadah secara merata. Setiap wadah memuat telur sebanyak ... butir
Perhatikan contoh perkembangbiakan secara vegatatif di bawah ini!
- Umbi lapis
- Umbi batang
- Cangkok
- Tunas adventif
- Merunduk
Perkembangbiakan secara vegetatif alami ditunjuk oleh nomor ....
Paragraf penutup yang sesuai untuk pidato kelulusan siswa yang disampaikan kepala sekolah adalah …