Bank Soal Matematika SMP Bilangan Berpangkat
Soal
Rangkuman

Bab 1 | Bilangan Berpangkat Bulat Positif | Matematika | Kelas 7
Selengkapnya



Soal Populer Hari Ini

sumber: tanya-tanya.com
Bagian fosfolipid bilayer yang bersifat hidrofobik ditunjukan nomor ....
Biologi
Level 11
Biologi
Sel
Struktur dan Fungsi Sel
Perhatikan grafik berikut.
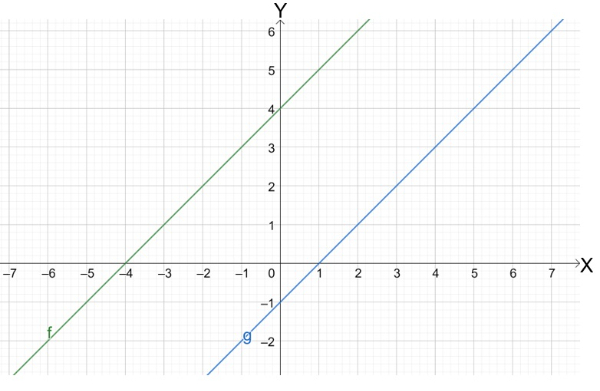
Translasi yang dapat memindahkan garis ke adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
The underlined expression expresses ....
Bahasa Inggris
Level 11
Good Advice
Giving Advice or Suggestions
Salah satu kegunaan senyawa hidrokarbon dalam kehidupan sehari-hari adalah proses pengelasan pada suatu logam. Pada proses pengelasan, digunakan suatu gas dari golongan alkuna yang merupakan hasil reaksi dari kalsium karbida dengan air. Gas yang dimaksud adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Diketahui adalah rumus dari
Jika benar untuk , maka ruas kiri menjadi ....
Matematika
Level 11
Logika
Induksi Matematika
Induksi Matematika pada Barisan Bilangan
Terdapat 3 buah partikel yang berada di titik koordinat berikut.

Partikel A dan B masing-masing bermassa 1 kg sementara partikel C bermassa 2 kg. Besar momen inersia sistem jika ketiga partikel diputar terhadap sumbu y adalah ....
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Dinamika Benda Tegar
Membran sel bersifat impermeabel terhadap molekul di bawah ini, kecuali ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Perhatikan struktur di bawah ini!
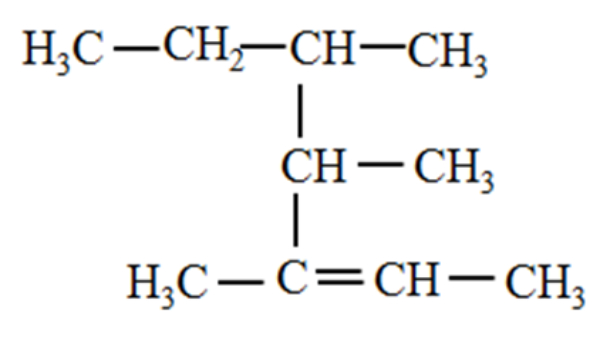
Tata nama dari struktur tersebut adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Jika dan adalah solusi dari persamaan trigonometri untuk dan maka nilai dari
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Berikut kebijakan yang bisa diambil sebuah negara untuk mengurangi dampak pemanasan global, kecuali ....
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal

sumber: tanya-tanya.com
Bagian fosfolipid bilayer yang bersifat hidrofobik ditunjukan nomor ....
Perhatikan grafik berikut.
Translasi yang dapat memindahkan garis ke adalah ....
The underlined expression expresses ....
Salah satu kegunaan senyawa hidrokarbon dalam kehidupan sehari-hari adalah proses pengelasan pada suatu logam. Pada proses pengelasan, digunakan suatu gas dari golongan alkuna yang merupakan hasil reaksi dari kalsium karbida dengan air. Gas yang dimaksud adalah ....
Diketahui adalah rumus dari
Jika benar untuk , maka ruas kiri menjadi ....
Terdapat 3 buah partikel yang berada di titik koordinat berikut.
Partikel A dan B masing-masing bermassa 1 kg sementara partikel C bermassa 2 kg. Besar momen inersia sistem jika ketiga partikel diputar terhadap sumbu y adalah ....
Membran sel bersifat impermeabel terhadap molekul di bawah ini, kecuali ....
Perhatikan struktur di bawah ini!
Tata nama dari struktur tersebut adalah ....
Jika dan adalah solusi dari persamaan trigonometri untuk dan maka nilai dari
Berikut kebijakan yang bisa diambil sebuah negara untuk mengurangi dampak pemanasan global, kecuali ....



