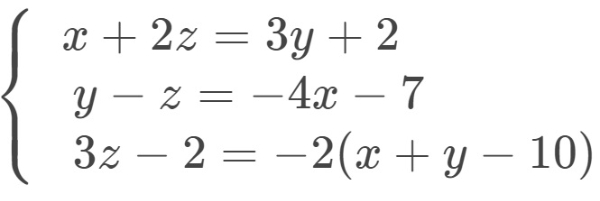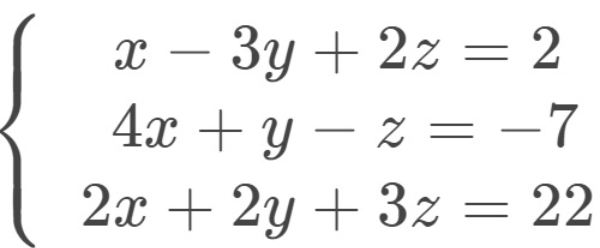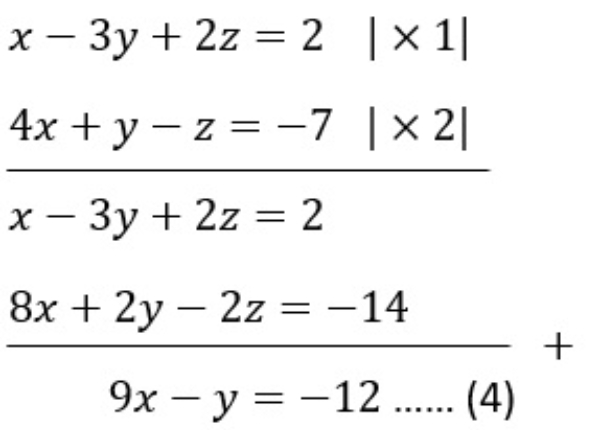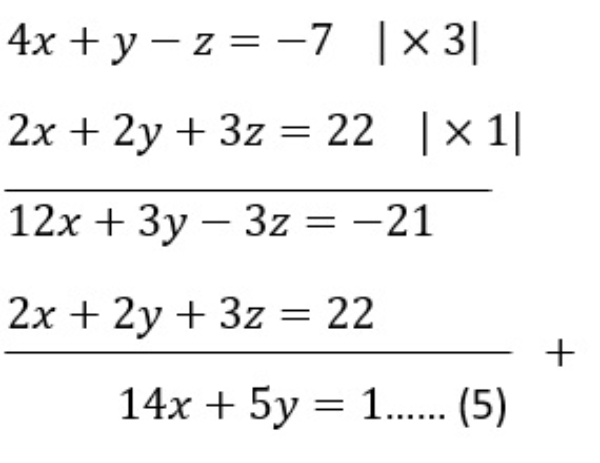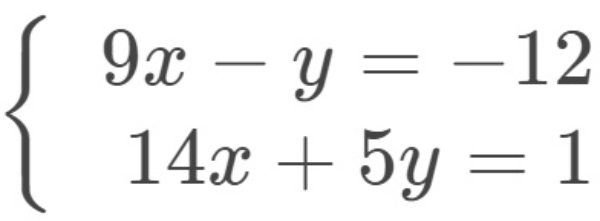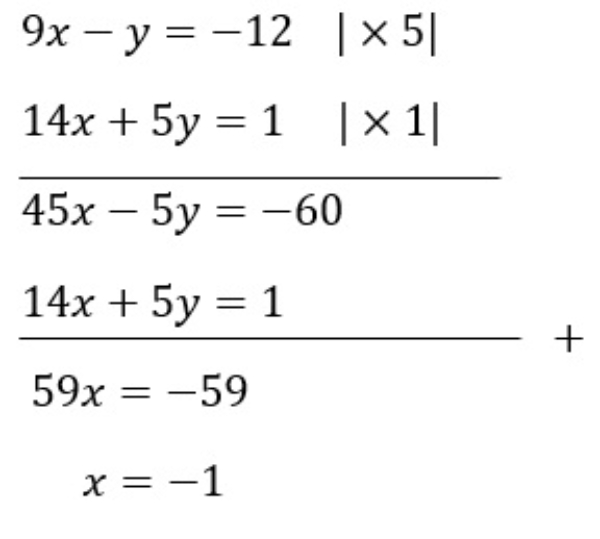Bank Soal Matematika SMA Sistem Persamaan Linear Tiga Variabel
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Terdapat bilangan:
3 ; 6 ; 5 ; 9 ; 10
Urutan bilangan dari yang terbesar adalah ....
Matematika
Level 1
Bilangan
Mengenal Bilangan Cacah (0-100)
Mengurutkan Bilangan
Sebaiknya kita sudah mulai belajar membaca sejak ....
Bahasa Indonesia
Level 1
Membaca
Membaca Permulaan
Persiapan Membaca
11 + 18 = ....
Matematika
Level 1
Bilangan
Penjumlahan dan Pengurangan Bilangan Cacah
Penjumlahan dan Pengurangan Bilangan Cacah
Lanjutkan urutan angka di bawah ini.
1, 3, 5, ....
Matematika
Level 1
Bilangan
Pola Bilangan
Memprediksi dan Membuat Pola Bilangan
Kegiatan yang membutuhkan waktu lebih lama, kecuali ....
Matematika
Level 1
Bilangan
Mengenal Satuan Waktu, Panjang, dan Berat
Membandingkan Lamanya Waktu
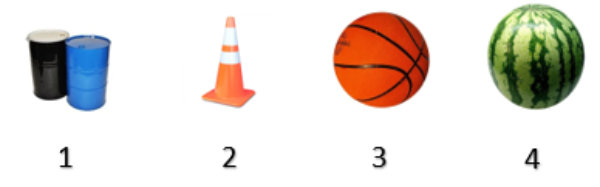
Benda yang bentuknya sama adalah nomor ....
Matematika
Level 1
Geometri
Mengenal Bangun Ruang
Macam-Macam Bangun Ruang
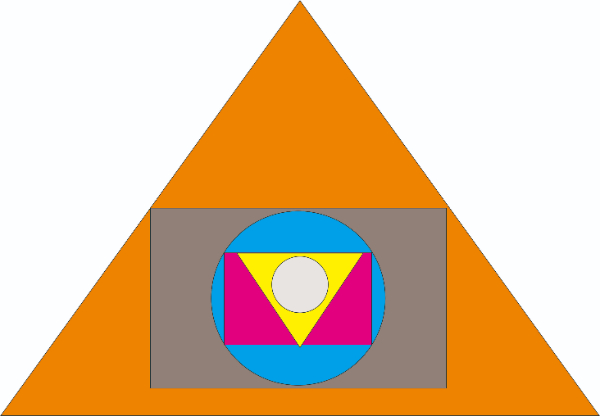
Pada gambar di atas terdapat 2 lingkaran dengan warna ....
Matematika
Level 1
Geometri
Mengenal Bangun Datar
Mengelompokkan Benda Berdasarkan Bentuk
Coki, Dodo, Erfan memilih sebuah bilangan.
Bilangan yang dipilih masing-masing, digambarkan sebagai berikut.

(Sumber Gambar: freepik.com)
Nama bilangan yang dipilih Erfan adalah ....
Matematika
Level 1
Bilangan
Mengenal Bilangan Cacah (0-100)
Lambang Bilangan
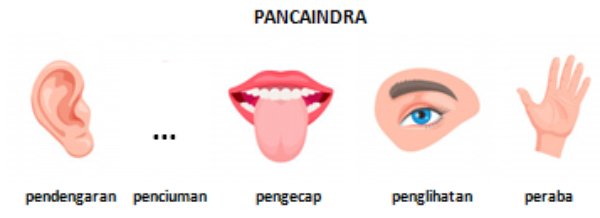
Gambar yang tepat untuk mengisi indra penciuman adalah ....
Bahasa Indonesia
Level 1
Menulis
Anggota Tubuh
Fungsi Anggota Tubuh (Pancaindra)
Bacalah teks percakapan berikut ini!
Tia: Ani, kamu berangkat sekolah pukul berapa?
Ani: Aku berangkat sekolah pukul 06.30. Bagaimana denganmu?
Tia: Aku juga berangkat sekolah pukul 06.30.
Ani: Tia, kamu tidur malam pukul berapa?
Tia: Aku tidur malam pukul 9 malam. Bagaimana denganmu?
Ani: Aku tidur malam pukul 10 malam.
Tia tidur malam pada pukul ....
Bahasa Indonesia
Level 1
Menulis
Kosakata Siang dan Malam
Kegiatan pada Waktu Siang dan Malam
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Terdapat bilangan:
3 ; 6 ; 5 ; 9 ; 10
Urutan bilangan dari yang terbesar adalah ....
Sebaiknya kita sudah mulai belajar membaca sejak ....
11 + 18 = ....
Lanjutkan urutan angka di bawah ini.
1, 3, 5, ....
Kegiatan yang membutuhkan waktu lebih lama, kecuali ....
Benda yang bentuknya sama adalah nomor ....
Pada gambar di atas terdapat 2 lingkaran dengan warna ....
Coki, Dodo, Erfan memilih sebuah bilangan.
Bilangan yang dipilih masing-masing, digambarkan sebagai berikut.
(Sumber Gambar: freepik.com)
Nama bilangan yang dipilih Erfan adalah ....
Gambar yang tepat untuk mengisi indra penciuman adalah ....
Bacalah teks percakapan berikut ini!
Tia: Ani, kamu berangkat sekolah pukul berapa?
Ani: Aku berangkat sekolah pukul 06.30. Bagaimana denganmu?
Tia: Aku juga berangkat sekolah pukul 06.30.
Ani: Tia, kamu tidur malam pukul berapa?
Tia: Aku tidur malam pukul 9 malam. Bagaimana denganmu?
Ani: Aku tidur malam pukul 10 malam.
Tia tidur malam pada pukul ....