Bank Soal Matematika SMA Peluang Kejadian Majemuk
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Pecahan yang senilai dengan pecahan di atas adalah ...
Matematika
Level 4
Bilangan
Pecahan
Pecahan Senilai

Keliling bangun pada gambar adalah … cm.
Matematika
Level 6
Geometri
Bangun Datar
Ulasan Buku Oliver Twist Karya Charles Dickens
Pada suatu ketika, hiduplah seorang anak yatim bernama Oliver Twist. Umurnya sembilan tahun. Ia hidup dalam roda kehidupan yang sangat berat.
Ia ditampung di panti asuhan. Pada saat makan, ia mengambil bubur tanpa seizin pemasak. Kepala panti asuhan mengatakan bahwa ia akan digantung. Kemudian, ia diambil oleh keluarga pembuat peti mati, Sowerberry.
Saat hidup di keluarga Sowerberry, ia juga tersiksa, tidur di bawah, diberi makan anjing, dan sebagainya. Suatu saat, anak keluarga Sowerberry menghina ibu Oliver dan Oliver pun marah. Pertengkaran pun tak terelakkan. Oliver dilaporkan polisi setempat, lalu paginya ia kabur, pergi ke London. Saat di perjalanan, Oliver jatuh pingsan. Ada seorang nenek tua renta yang menolong Oliver karena merasa tak tega.

Sampul buku Oliver Twist karya Charles Dickens, diterbitkan oleh Bentang Pustaka
Novel ini bercerita mengenai seorang anak yang tinggal di rumah penampungan, kemudian memilih kabur dan hidup di jalanan. Latar ceritanya berada di Kota London pada tahun 1873.
Gaya bahasa yang digunakan dalan novel ini mudah dipahami dan tidak terlalu rumit. Tokoh dalam novel juga digambarkan mempunyai karakter yang kuat. Namun, novel ini punya sisi membosankan, yaitu penjelasan tiap adegannya yang terlalu rinci.
Novel ini baik untuk dibaca anak-anak karena mengajarkan untuk peduli pada teman, saudara, dan tetangga yang hidupnya kekurangan. Tokoh dalam novel ini juga mengajarkan kegigihan dalam bertahan hidup, dalam melewati segala cobaan.
(Dikutip dari berbagai sumber)
Pelajaran yang bisa diambil dari novel Oliver Twist adalah ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra

Fill in the blank with the correct verb.
She is a dancer. She ____ on the stage.
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Simple Present Tense
Bilangan kelipatan 8 yang kurang dari 30 adalah ...
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Kelipatan Bilangan
Ayah Anton membeli sebuah hadiah yang di dalamnya terdapat kartu ucapan berbentuk segi banyak untuk Anton dan adiknya. Anton mendapat sebuah kartu ucapan berbentuk segi delapan. Adik Anton tidak tahu nama bentuk dari kartu ucapannya. Jumlah kedua sisi kartu ucapan tersebut adalah 12. Kartu ucapan adik Anton berbentuk ...
Matematika
Level 4
Geometri
Bangun Datar
Segi Banyak
2 x 32 x 52 adalah faktorisasi dari ....
Matematika
Level 4
Bilangan
FPB dan KPK
Faktor dan Faktorisasi Prima
Cermati teks berikut!
Jaka Tarub

Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Tokoh utama dari cerita di atas adalah ....
Bahasa Indonesia
Level 4
Membaca
Teks Fiksi-Tokoh Cerita
Cerita Rakyat
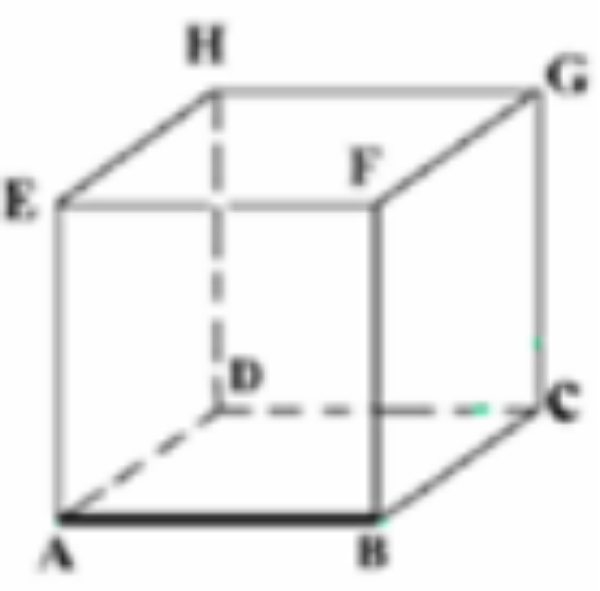
Berdasarkan kubus ABCD.EFGH, bidang yang berpotongan adalah ...
Matematika
Level 4
Geometri
Garis dan Sudut
Hubungan Antar Garis
Berikut adalah diagram batang dari hasil panen kebun Kakek.
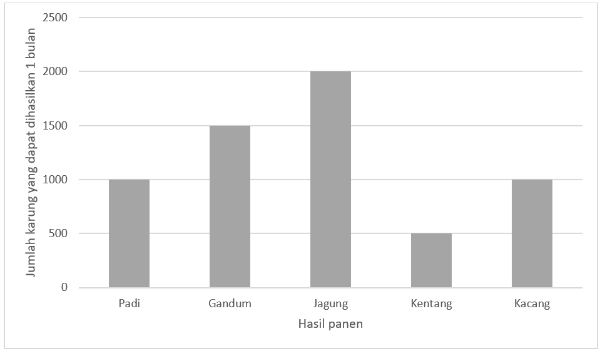
Berapa jumlah karung seluruh hasil panen kebun Kakek setiap 1 bulan?
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Pecahan yang senilai dengan pecahan di atas adalah ...
Keliling bangun pada gambar adalah … cm.
Ulasan Buku Oliver Twist Karya Charles Dickens
Pada suatu ketika, hiduplah seorang anak yatim bernama Oliver Twist. Umurnya sembilan tahun. Ia hidup dalam roda kehidupan yang sangat berat.
Ia ditampung di panti asuhan. Pada saat makan, ia mengambil bubur tanpa seizin pemasak. Kepala panti asuhan mengatakan bahwa ia akan digantung. Kemudian, ia diambil oleh keluarga pembuat peti mati, Sowerberry.
Saat hidup di keluarga Sowerberry, ia juga tersiksa, tidur di bawah, diberi makan anjing, dan sebagainya. Suatu saat, anak keluarga Sowerberry menghina ibu Oliver dan Oliver pun marah. Pertengkaran pun tak terelakkan. Oliver dilaporkan polisi setempat, lalu paginya ia kabur, pergi ke London. Saat di perjalanan, Oliver jatuh pingsan. Ada seorang nenek tua renta yang menolong Oliver karena merasa tak tega.
Sampul buku Oliver Twist karya Charles Dickens, diterbitkan oleh Bentang Pustaka
Novel ini bercerita mengenai seorang anak yang tinggal di rumah penampungan, kemudian memilih kabur dan hidup di jalanan. Latar ceritanya berada di Kota London pada tahun 1873.
Gaya bahasa yang digunakan dalan novel ini mudah dipahami dan tidak terlalu rumit. Tokoh dalam novel juga digambarkan mempunyai karakter yang kuat. Namun, novel ini punya sisi membosankan, yaitu penjelasan tiap adegannya yang terlalu rinci.
Novel ini baik untuk dibaca anak-anak karena mengajarkan untuk peduli pada teman, saudara, dan tetangga yang hidupnya kekurangan. Tokoh dalam novel ini juga mengajarkan kegigihan dalam bertahan hidup, dalam melewati segala cobaan.
(Dikutip dari berbagai sumber)
Pelajaran yang bisa diambil dari novel Oliver Twist adalah ....

Fill in the blank with the correct verb.
She is a dancer. She ____ on the stage.
Bilangan kelipatan 8 yang kurang dari 30 adalah ...
Ayah Anton membeli sebuah hadiah yang di dalamnya terdapat kartu ucapan berbentuk segi banyak untuk Anton dan adiknya. Anton mendapat sebuah kartu ucapan berbentuk segi delapan. Adik Anton tidak tahu nama bentuk dari kartu ucapannya. Jumlah kedua sisi kartu ucapan tersebut adalah 12. Kartu ucapan adik Anton berbentuk ...
2 x 32 x 52 adalah faktorisasi dari ....
Cermati teks berikut!
Jaka Tarub
Suatu malam, Jaka Tarub bermimpi makan daging rusa yang lezat. Paginya Jaka Tarub pergi ke hutan untuk berburu rusa. Alih-alih rusa, yang ditemukan malah tujuh bidadari cantik yang sedang mandi di telaga. Dengan mengendap-endap, Jaka Tarub mengambil salah satu selendang bidadari yang ada di pinggir telaga. Karena tidak dapat pulang ke kahyangan tanpa selendangnya, Nawang Wulan terpaksa ditinggal oleh kakak-kakaknya.
Nawang Wulan yang bersedih hati karena ditinggal pun bersedia ikut Jaka Tarub pulang ke rumahnya. Tak lama kemudian, mereka pun menikah. Anak perempuan pertama mereka, Nawangsih, terlahir setelahnya. Sejak adanya Nawang Wulan dan Nawangsih, Jaka Tarub merasa hidupnya bahagia kembali.
Sejak pernikahannya dengan Nawang Wulan, Jaka Tarub merasakan adanya satu keanehan. Hal ini yaitu lumbung padinya tidak pernah berkurang meskipun selalu diambil berasnya untuk memasak nasi. Meski diminta berjanji untuk tidak mencari tahu, Jaka Tarub melanggar janjinya sendiri dengan mengintip periuk nasi yang sedang dimasak Nawang Wulan. Akibatnya, kekuatan Nawang Wulan pun hilang. Sejak itu ia harus menumbuk dan menampi beras seperti manusia lainnya. Akibatnya lumbung padi Jaka Tarub terus berkurang.
Suatu hari Nawang Wulan menemukan selendangnya yang sudah lama hilang di dalam lumbung. Nawang Wulan lalu memutuskan kembali ke kahyangan dengan selendangnya. Sebelum berangkat ke kahyangan, Nawang Wulan berpesan pada Jaka Tarub untuk meninggalkan Nawangsih di dekat rumahnya tiap malam. Setiap malam Nawang Wulan turun menghampiri Nawangsih dan kembali ke kahyangan menjelang pagi. Demikian hal ini terus berlanjut hingga Nawangsih beranjak dewasa. Setelahnya, Nawang Wulan tidak pernah lagi turun ke bumi dan Jaka Tarub tidak pernah bertemu dengannya lagi.
Tokoh utama dari cerita di atas adalah ....
Berdasarkan kubus ABCD.EFGH, bidang yang berpotongan adalah ...
Berikut adalah diagram batang dari hasil panen kebun Kakek.
Berapa jumlah karung seluruh hasil panen kebun Kakek setiap 1 bulan?



