Bank Soal Matematika SMA Persamaan Garis Singgung dan Garis Normal Kurva
Soal
Video Matematika Wajib LOTS
Video
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Nilai y pada persamaan
−5y − 180 = 60 − (−7y) adalah ....
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Persamaan Linear Satu Variabel (PLSV)
73= ...
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
S = {0, 1, 2, …, 9}
A = {8, 7, 1}
B = {1, 2, 9}
C = {1, 7}
D = {0}
S adalah …
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Perhatikan gambar berikut!
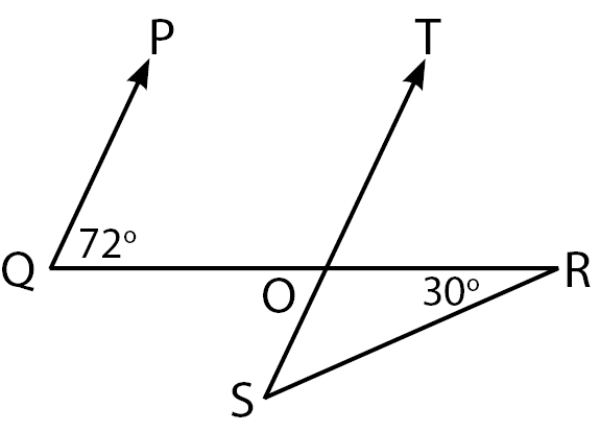
Besar RSO yang memenuhi gambar di atas adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Hubungan Antar Sudut
Keindahan yang ditonjolkan dari Pulau Tomia berdasarkan teks deskripsi tersebut adalah ….
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Menentukan Isi Teks Deskripsi
Hasil dari:
Matematika
Level 7
Aljabar
Bentuk Aljabar
Operasi Hitung Bentuk Aljabar
Surat dinas adalah surat ....
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Ciri Surat Pribadi dan Surat Dinas
Perhatikan penggalan buku fiksi berikut.
Hiruk pikuk bunyi kendaraan mulai memecahkan keheningan pagi. Jalan Veteran mulai ramai dipenuhi angkutan kota yang lalu-lalang. Ada yang pergi bekerja, ada yang hanya sekadar berjalan-jalan pagi. Ada yang ingin berangkat sekolah. Semuanya terlihat terburu-buru.
(Dikutip dari novel Origami Hati karya Boy Candra)
Unsur yang menonjol pada penggalan buku fiksi tersebut adalah ….
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Unsur Pembangun Buku Fiksi dan Nonfiksi
Diagram batang di bawah ini menunjukkan hasil produksi bulan Januari-Juni. Hasil produksi yang mengalami penurunan adalah bulan …
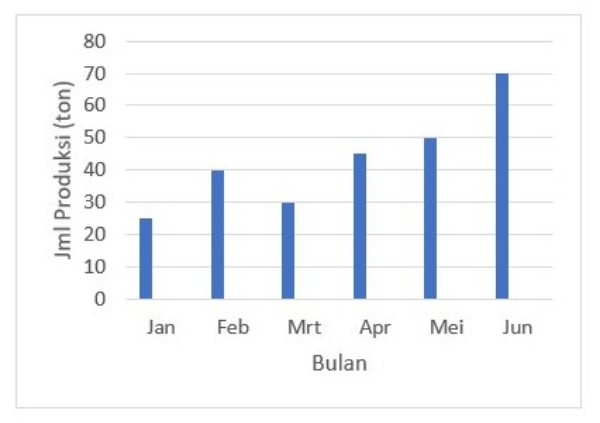
Matematika
Level 5
Statistika
Penyajian dan Pengolahan Data
Penyajian dan Pengolahan Data
We say 'What do you do' when we want to know someone's ....
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Self Introduction
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Nilai y pada persamaan
−5y − 180 = 60 − (−7y) adalah ....
73= ...
S = {0, 1, 2, …, 9}
A = {8, 7, 1}
B = {1, 2, 9}
C = {1, 7}
D = {0}
S adalah …
Perhatikan gambar berikut!
Besar RSO yang memenuhi gambar di atas adalah ....
Keindahan yang ditonjolkan dari Pulau Tomia berdasarkan teks deskripsi tersebut adalah ….
Hasil dari:
Surat dinas adalah surat ....
Perhatikan penggalan buku fiksi berikut.
Hiruk pikuk bunyi kendaraan mulai memecahkan keheningan pagi. Jalan Veteran mulai ramai dipenuhi angkutan kota yang lalu-lalang. Ada yang pergi bekerja, ada yang hanya sekadar berjalan-jalan pagi. Ada yang ingin berangkat sekolah. Semuanya terlihat terburu-buru.
(Dikutip dari novel Origami Hati karya Boy Candra)
Unsur yang menonjol pada penggalan buku fiksi tersebut adalah ….
Diagram batang di bawah ini menunjukkan hasil produksi bulan Januari-Juni. Hasil produksi yang mengalami penurunan adalah bulan …
We say 'What do you do' when we want to know someone's ....



