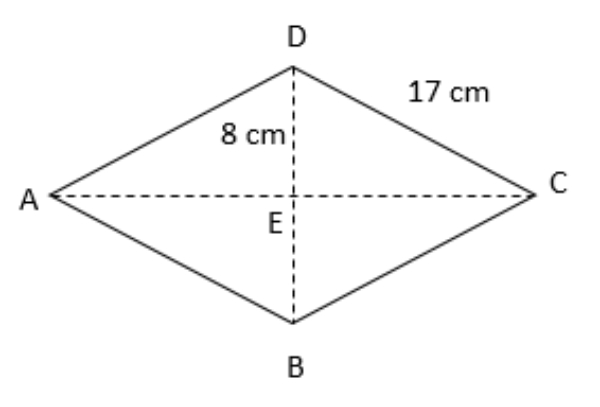
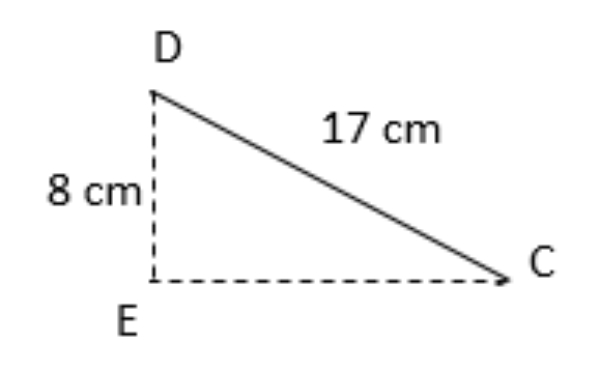
Bank Soal Matematika SMP Penerapan Teorema Pythagoras

Soal

Pilgan

Luas belah ketupat pada gambar berikut adalah ....

A

240 cm2

B

280 cm2

C

320 cm2

D

360 cm2

Pembahasan:

Diketahui:

Belah ketupat ABCD berikut.

Ditanya:

Luas belah ketupat ABCD?

Jawab:

Perhatikan △DEC\triangle DEC berikut!

Berdasarkan Teorema Pythagoras diperoleh

CD2=EC2+DE2CD^2=EC^2+DE^2

EC2=CD2−DE2EC^2=CD^2-DE^2

EC=CD2−DE2EC=\sqrt{CD^2-DE^2}

EC=172−82EC=\sqrt{17^2-8^2}

EC=289−64EC=\sqrt{289-64}

EC=225EC=\sqrt{225}

EC=15EC=15

Perlu diingat kembali sifat belah ketupat yaitu, kedua diagonalnya saling memotong sama panjang. Artinya,

AE=EC=4AE=EC=4 dan

BE=DE=8BE=DE=8 .

Sehingga diperoleh diagonal belah ketupat, yaitu

d1=AC=AE+EC=15+15=30d_1=AC=AE+EC=15+15=30 cm

d2=BD=BE+DE=8+8=16d_2=BD=BE+DE=8+8=16 cm

Rumus luas belah ketupat adalah

L=d1×d22L=\frac{d_1\times d_2}{2}

L=30×162L=\frac{30\times16}{2}

L=240L=240 cm2

K13 Kelas VIII Matematika Geometri Teorema Pythagoras Penerapan Teorema Pythagoras Skor 3
Teknik Hitung LOTS
Video
07 Desember 2020
Penerapan Teorema Pythagoras | Matematika | Kelas VIII
✔ Ingin tanya tutor?
✔ Cek sampel tanya jawab
Rangkuman
08 April 2020
Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya
Lihat Semua Rangkuman dan Materi

Siswa

Ingin latihan soal, nonton, atau unduh materi belajar lebih banyak?

Buat Akun Gratis

Guru

Ingin akses bank soal, nonton, atau unduh materi belajar lebih banyak?

Buat Akun Gratis

Soal Populer Hari Ini

Diketahui persamaan 5(3x + 8) = 2 (3x + 2), maka nilai x2^2 adalah ....

Matematika Level 7 Aljabar Persamaan dan Pertidaksamaan Linear Satu Variabel Persamaan Linear Satu Variabel (PLSV) Kelas VII Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Penulisan kata berimbuhan me- yang tidak tepat adalah ….

Bahasa Indonesia Level 7,7 Menulis Teks Deskripsi Struktur dan Kebahasaan Teks Deskripsi Kelas VII Kurikulum 2013 K13 Bahasa Indonesia
Lihat selengkapnya

Perhatikan tabel berikut!

Berdasarkan tabel tersebut, pasangan jenis buku dan contohnya yang tepat adalah ….

Bahasa Indonesia Level 7 Menulis Buku Fiksi dan Nonfiksi Unsur Pembangun Buku Fiksi dan Nonfiksi KD3.9 Kelas VII Kurikulum 2013 K13 Bahasa Indonesia
Lihat selengkapnya

Jika di dalam surat dinas ada kop surat, maka bagian yang tidak perlu dicantumkan adalah ....

Bahasa Indonesia Level 7 Menulis Surat Pribadi dan Surat Dinas Unsur-unsur dan Kebahasaan Surat KD3.12 Kelas VII Kurikulum 2013 K13 Bahasa Indonesia
Lihat selengkapnya

Bentuk paling sederhana dari

x2−368x−56÷x2+14x+484x−28=\frac{x^2-36}{8x-56}\div\frac{x^2+14x+48}{4x-28}= ....

Matematika Level 7 Aljabar Bentuk Aljabar Operasi Pecahan Bentuk Aljabar Kelas VII Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Study the picture of a family tree below.

picture: Buku Bahasa Inggris 'When English Rings a Bell'

Hi, my name is Beni. Above is my family tree. There are nine people in my family. My brother is Indra, and my sister is Siti. My mother is Hasanah, and my father is Didi. I have an uncle and an auntie. They are Johan and Yuli. I also live with my grandparents, Sarah and Ridwan.

Didi is my ....

Bahasa Inggris Level 7 Bahasa Inggris Describing oneself Vocabulary: Family Tree Kelas VII Kurikulum 2013 K13
Lihat selengkapnya

Kegiatan di bawah ini merupakan proses yang dilakukan dalam statistika, kecuali ....

Matematika Level 7 Statistika Penyajian dan Pengolahan Data Penyajian dan Pengolahan Data Kelas VII Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Diketahui ruas garis DF dengan panjang 56 cm. Titik E terletak di antara titik D dan F sehingga DE : EF = 3 : 5. Panjang DE adalah ....

Matematika Level 7 Geometri Garis dan Sudut Perbandingan Ruas Garis Video Kelas VII Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Perhatikan teks berikut!

Roni membeli sebuah hadiah yang diperuntukkan kepada adiknya. Hadiah tersebut dibungkus, dengan sangat rapih dengan kertas kado bermotif bunga-bunga berwarna-warni. Diatas bungkus kado tersebut ditambahkan sebuah pita kecil. Adik Roni merasa begitu bahagianya saat menerima hadiah dari Kakaknya. 

Perbaiki teks deskripsi di atas sehingga menjadi kalimat yang efektif!

Bahasa Indonesia Level 7 Menulis Teks Deskripsi Struktur dan Kebahasaan Teks Deskripsi KD3.2 Kelas VII Kurikulum 2013 K13 Bahasa Indonesia
Lihat selengkapnya

Sebuah piringan hitam berputar 45 putaran per menit selama 13 menit. Berapa lama piringan hitam berputar jika kecepatan putarannya 90 putaran per menit?

Matematika Level 7 Pengukuran Perbandingan Perbandingan Senilai dan Berbalik Nilai Kelas VII Kurikulum 2013 K13 Matematika
Lihat selengkapnya
✔ Ingin soal latihan HOTS?
✔ Cek sampel soal HOTS?

Cek Contoh Kuis Online

Kejar Kuis

Cek Contoh Bank Soal

Kejar Soal