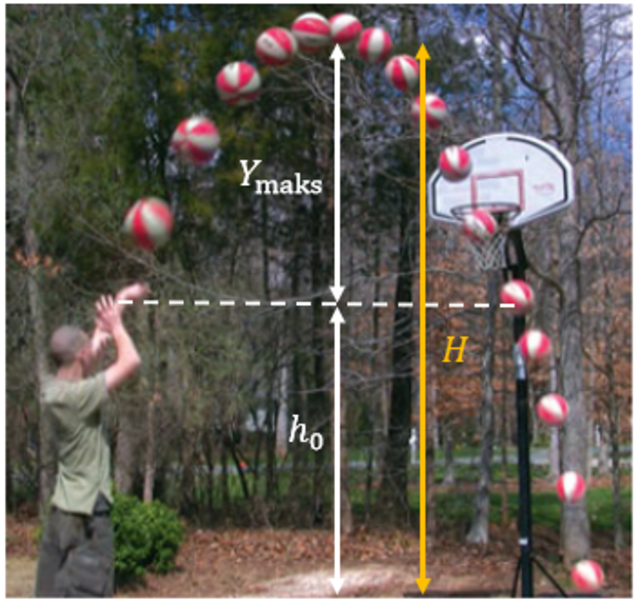
Bank Soal Fisika SMA Gerak Parabola
Soal
Soal Populer Hari Ini
Read the text carefully.

PANCAKES
Serve with a little caster sugar or lemon juice.
This recipe is for 2 adults and 2 kids.
Preparation time: 10 minutes
Cooking time: 15 minutes
Ingredients:
- 225 g of plain flour
- 1 egg
- 425 ml of low-fat milk
- Pinch of salt if desired
Methods:
- Sieve the flour and salt into a bowl
- Make a hoe in the center of the flour and drop in the egg with ¼ of the milk.
- Stir the egg mixture in the center of the bowl with a wooden spoon, allowing the flour to fall in gradually from the sides.
- Add the rest of the milk slowly, beating well avoid lumps.
- Pour a thin layer of the mixture onto a hot, non-stick pan.
- Use a spatula to turn the pancake over when bubbles start to appear on top.
Savory Fillings
- Chopped cooked chicken
- Smoked haddock
- Tinned salmon
- Mushrooms
- Mince cooked in curry sauce
- Bolognese sauce
Sweet Fillings
- Jam
- Stewed fruit
- Fried bananas
Source: 101 Square Meals by Safe Food
The recipe can be served for ... people.
Bahasa Inggris
Level 9
Bahasa Inggris
How to do or make things
Procedure Text
Kelas IX
Kurikulum 2013
K13
Here is the data from the Kejarcita English Club member about the genre of movie watched last month.
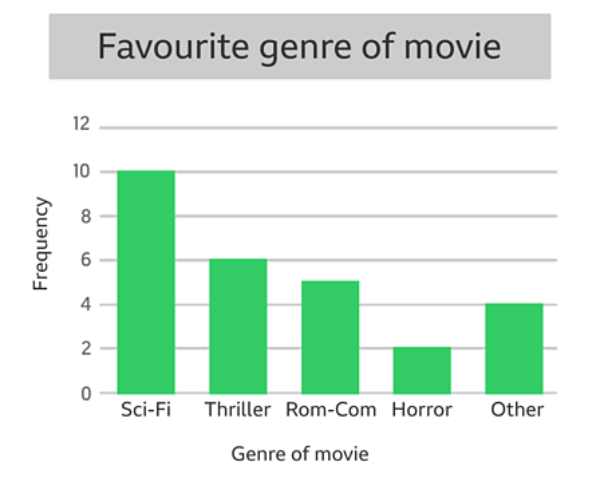
Source: bbc.co.uk
What is the most suitable statement based on the Sci-Fi genre data?
Bahasa Inggris
Level 9
Bahasa Inggris
Using passive voice to describe things
Passive Voice
Kelas IX
Kurikulum 2013
K13
Alat dan Bahan
1. 1 buah mikroskop
2. 1 buah cover glass
3. 1 buah objek glass
4. Preparat daun zea mays (jagung)
Yang dimaksud dengan bahan di dalam cuplikan teks tersebut adalah ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Identifikasi Laporan Percobaan
KD3.1
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Penjabaran yang benar dari adalah ...
Matematika
Level 9
Bilangan
Bilangan Berpangkat dan Bentuk Akar
Bilangan Berpangkat
Kelas IX
Kurikulum 2013
K13
Matematika
Baca teks berikut ini dengan cermat.
Pro dan Kontra Warga Jakarta Menyikapi Penerapan Tilang ETLE
Penerbitan aturan berkendara di jalan belum begitu efektif membuat para pengendara motor patuh. Meskipun sudah ada personel polisi yang bertugas menertibkan lalu lintas, masih banyak pengendara yang bandel. Berangkat dari permasalahan tersebut, Kepolisian Daerah Metropolitan Jakarta Raya (Polda Metro Jaya) menerapkan sistem tilang elektronik atau ETLE (electronic traffic law enforcement). ETLE rencananya mulai diperluas pada Februari 2020.
Tilang elektronik akan diterapkan di beberapa titik di Jakarta dan Bekasi. Penerapan tilang tersebut dilakukan dengan memasang kamera-kamera di beberapa bahu jalan untuk merekam pelanggaran yang dilakukan oleh pengendara motor. Foto dan video dari kamera ETLE nantinya akan diverifikasi oleh petugas dan akan dikirim ke rumah pengendara yang melanggar.
Meskipun program ETLE bertujuan baik, masih ada masyarakat yang kurang setuju. Jaenal, seorang pengemudi ojek online asal Kebon Jeruk, kurang setuju dengan adanya tilang format baru tersebut. Jaenal merasa tilang ETLE akan merugikannya ketika mencari dan mendapatkan penumpang. "Saya kurang setuju dengan tilang eletronik. Kalau kebetulan saya lewat Bundaran Senayan Ratu Plaza (Salah satu titik kamera ETLE) sambil megang handphone karena menghubungi penumpang bagaimana?" ujar Jaenal.
Di sisi lain, banyak pihak yang sepakat dengan penerapan tilang ETLE. Johan, pemuda asal Pondok Gede justru lebih menyukai sistem tilang ETLE. "Iya, kalau tilang yang ketemu polisi langsung kan suka ada transaksi ilegal, jadi kurang adil," ujar Johan. Ada juga Abidin yang berpendapat kalau tilang ETLE lebih efektif daripada tilang Ditlantas turun ke jalan. "Kalau yang ditangkap kamera kan lebih jelas pelanggarannya apa. Kalau yang tilang langsung di jalan kadang suka cari-cari kesalahan, kadang harus mengeluarkan uang lebih," ujar Abidin.
Karena persoalannya adalah lalu lintas jalanan umum, maka yang harus diutamakan adalah kebaikan pengendara. Tilang ETLE hadir untuk meningkatkan ketertiban sekaligus keselamatan di jalan. Oleh karena itu bagi pengendara yang melakukan aktivitas lain ketika di jalan, sebaiknya berhenti atau minggir terlebih dahulu. Masyarakat dan polisi diharapkan saling bekerja sama menjaga ketertiban dan keselamatan dalam berlalu lintas.
(Sumber: Kompas.com, dengan penyesuaian)
Alasan diadakannya sistem tilang elektronik atau ETLE adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Menggali Informasi Teks Diskusi
KD3.9
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Kalimat berikut ini mengandung istilah bidang ilmu, kecuali ...
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Struktur dan Kebahasaan Laporan Percobaan
KD3.2
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Baca teks berikut ini dengan cermat.
Gagasan dan inisiatif Pak Kinong melalui bemo bacanya berhasil menarik perhatian publik. (1) Banyak anak muda, terutama mahasiswa, yang kagum dengan tindakan Pak Kinong. (2) Bahkan Presiden Joko Widodo menunjukkan apresiasinya dengan mengundangnya ke Istana Negara pada peringatan Hari Pendidikan Nasional, 2 Mei 2017. (3) Yang lebih mengejutkan lagi ialah hadiah sebuah tiket umroh yang diberikan oleh presiden kepada Pak Kinong. (4) Selain itu, beberapa media juga mengundang Pak Kinong untuk menjadi narasumber mengenai perjuangannya menumbuhkan minat baca.
(Sumber: Kompas.com, dengan penyesuaian)
Sikap simpati dalam kutipan cerita di atas ditunjukkan pada kalimat nomor ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
KD4.12
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Pernyataan yang benar mengenai simpulan teks diskusi adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Struktur dan Kebahasaan Teks Diskusi
KD4.9
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Baca teks berikut ini dengan cermat.
Bocah bernama Zhang Ze mengalami kelumpuhan pada kakinya yang membuatnya tidak bisa berjalan secara normal. Namun, dia masih bisa berangkat ke sekolah tanpa mengalami kendala berkat temannya yang bernama Xu Bingyang. Xu Bingyang adalah temannya yang baik, yang menggendongnya setiap hari selama enam tahun.
(Sumber: Liputan6.com dengan penyesuaian)
Kutipan teks di atas merupakan bagian abstrak dalam cerita inspiratif. Bagian komplikasi yang tepat untuk melengkapi teks di atas adalah ...
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
KD4.12
Kelas IX
Kurikulum 2013
K13
Bahasa Indonesia
Read the following text and answer the question.
Hi, how's life?
I know it's been so tiring to stay at and manage everything from home for these two months. Everything starts being a normal thing, as we get used to it. I heard that your city has turned into a red zone right now, and I feel so sorry to hear that. I hope that all of your family members are okay and can get through this pandemic. Let us hope that everything goes back to normal. We are stronger than the virus.
With love,
Ama
The writer's intention in writing the text is to ....
Bahasa Inggris
Level 9
Bahasa Inggris
Appreciation over achievements or happiness
Expressions of Wishes, Prayers
Kelas IX
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Read the text carefully.
PANCAKES
Serve with a little caster sugar or lemon juice.
This recipe is for 2 adults and 2 kids.
Preparation time: 10 minutes
Cooking time: 15 minutes
Ingredients:
- 225 g of plain flour
- 1 egg
- 425 ml of low-fat milk
- Pinch of salt if desired
Methods:
- Sieve the flour and salt into a bowl
- Make a hoe in the center of the flour and drop in the egg with ¼ of the milk.
- Stir the egg mixture in the center of the bowl with a wooden spoon, allowing the flour to fall in gradually from the sides.
- Add the rest of the milk slowly, beating well avoid lumps.
- Pour a thin layer of the mixture onto a hot, non-stick pan.
- Use a spatula to turn the pancake over when bubbles start to appear on top.
Savory Fillings
- Chopped cooked chicken
- Smoked haddock
- Tinned salmon
- Mushrooms
- Mince cooked in curry sauce
- Bolognese sauce
Sweet Fillings
- Jam
- Stewed fruit
- Fried bananas
Source: 101 Square Meals by Safe Food
The recipe can be served for ... people.
Here is the data from the Kejarcita English Club member about the genre of movie watched last month.
Source: bbc.co.uk
What is the most suitable statement based on the Sci-Fi genre data?
Alat dan Bahan
1. 1 buah mikroskop
2. 1 buah cover glass
3. 1 buah objek glass
4. Preparat daun zea mays (jagung)
Yang dimaksud dengan bahan di dalam cuplikan teks tersebut adalah ....
Penjabaran yang benar dari adalah ...
Baca teks berikut ini dengan cermat.
Pro dan Kontra Warga Jakarta Menyikapi Penerapan Tilang ETLE
Penerbitan aturan berkendara di jalan belum begitu efektif membuat para pengendara motor patuh. Meskipun sudah ada personel polisi yang bertugas menertibkan lalu lintas, masih banyak pengendara yang bandel. Berangkat dari permasalahan tersebut, Kepolisian Daerah Metropolitan Jakarta Raya (Polda Metro Jaya) menerapkan sistem tilang elektronik atau ETLE (electronic traffic law enforcement). ETLE rencananya mulai diperluas pada Februari 2020.
Tilang elektronik akan diterapkan di beberapa titik di Jakarta dan Bekasi. Penerapan tilang tersebut dilakukan dengan memasang kamera-kamera di beberapa bahu jalan untuk merekam pelanggaran yang dilakukan oleh pengendara motor. Foto dan video dari kamera ETLE nantinya akan diverifikasi oleh petugas dan akan dikirim ke rumah pengendara yang melanggar.
Meskipun program ETLE bertujuan baik, masih ada masyarakat yang kurang setuju. Jaenal, seorang pengemudi ojek online asal Kebon Jeruk, kurang setuju dengan adanya tilang format baru tersebut. Jaenal merasa tilang ETLE akan merugikannya ketika mencari dan mendapatkan penumpang. "Saya kurang setuju dengan tilang eletronik. Kalau kebetulan saya lewat Bundaran Senayan Ratu Plaza (Salah satu titik kamera ETLE) sambil megang handphone karena menghubungi penumpang bagaimana?" ujar Jaenal.
Di sisi lain, banyak pihak yang sepakat dengan penerapan tilang ETLE. Johan, pemuda asal Pondok Gede justru lebih menyukai sistem tilang ETLE. "Iya, kalau tilang yang ketemu polisi langsung kan suka ada transaksi ilegal, jadi kurang adil," ujar Johan. Ada juga Abidin yang berpendapat kalau tilang ETLE lebih efektif daripada tilang Ditlantas turun ke jalan. "Kalau yang ditangkap kamera kan lebih jelas pelanggarannya apa. Kalau yang tilang langsung di jalan kadang suka cari-cari kesalahan, kadang harus mengeluarkan uang lebih," ujar Abidin.
Karena persoalannya adalah lalu lintas jalanan umum, maka yang harus diutamakan adalah kebaikan pengendara. Tilang ETLE hadir untuk meningkatkan ketertiban sekaligus keselamatan di jalan. Oleh karena itu bagi pengendara yang melakukan aktivitas lain ketika di jalan, sebaiknya berhenti atau minggir terlebih dahulu. Masyarakat dan polisi diharapkan saling bekerja sama menjaga ketertiban dan keselamatan dalam berlalu lintas.
(Sumber: Kompas.com, dengan penyesuaian)
Alasan diadakannya sistem tilang elektronik atau ETLE adalah ....
Kalimat berikut ini mengandung istilah bidang ilmu, kecuali ...
Baca teks berikut ini dengan cermat.
Gagasan dan inisiatif Pak Kinong melalui bemo bacanya berhasil menarik perhatian publik. (1) Banyak anak muda, terutama mahasiswa, yang kagum dengan tindakan Pak Kinong. (2) Bahkan Presiden Joko Widodo menunjukkan apresiasinya dengan mengundangnya ke Istana Negara pada peringatan Hari Pendidikan Nasional, 2 Mei 2017. (3) Yang lebih mengejutkan lagi ialah hadiah sebuah tiket umroh yang diberikan oleh presiden kepada Pak Kinong. (4) Selain itu, beberapa media juga mengundang Pak Kinong untuk menjadi narasumber mengenai perjuangannya menumbuhkan minat baca.
(Sumber: Kompas.com, dengan penyesuaian)
Sikap simpati dalam kutipan cerita di atas ditunjukkan pada kalimat nomor ....
Pernyataan yang benar mengenai simpulan teks diskusi adalah ....
Baca teks berikut ini dengan cermat.
Bocah bernama Zhang Ze mengalami kelumpuhan pada kakinya yang membuatnya tidak bisa berjalan secara normal. Namun, dia masih bisa berangkat ke sekolah tanpa mengalami kendala berkat temannya yang bernama Xu Bingyang. Xu Bingyang adalah temannya yang baik, yang menggendongnya setiap hari selama enam tahun.
(Sumber: Liputan6.com dengan penyesuaian)
Kutipan teks di atas merupakan bagian abstrak dalam cerita inspiratif. Bagian komplikasi yang tepat untuk melengkapi teks di atas adalah ...
Read the following text and answer the question.
Hi, how's life?
I know it's been so tiring to stay at and manage everything from home for these two months. Everything starts being a normal thing, as we get used to it. I heard that your city has turned into a red zone right now, and I feel so sorry to hear that. I hope that all of your family members are okay and can get through this pandemic. Let us hope that everything goes back to normal. We are stronger than the virus.
With love,
Ama
The writer's intention in writing the text is to ....