Bank Soal Matematika SMA Operasi Komposisi pada Fungsi
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Sebuah dadu dilempar 1 kali. Peluang muncul mata dadu bilangan prima genap adalah...
Matematika
Level 8
Statistika
Peluang
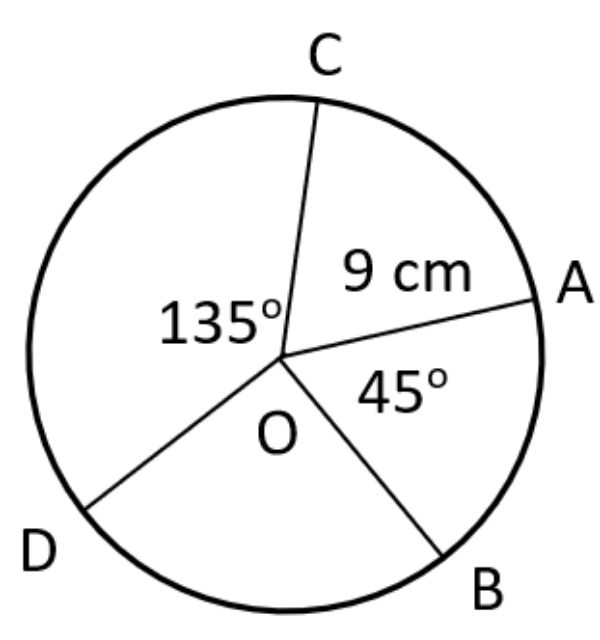
Jika panjang busur AB adalah 15 cm, maka panjang busur CD adalah ... cm
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
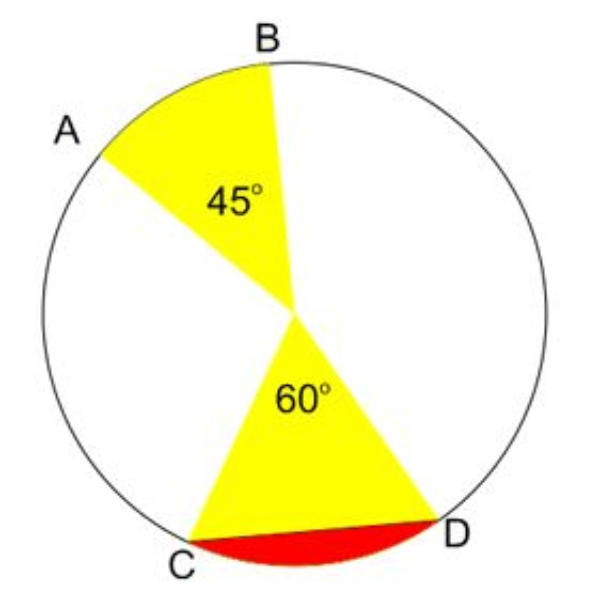
Perhatikan gambar lingkaran di atas, apabila panjang busur AB = 33 cm dan luas juring COD = 924 cm2, maka tentukanlah panjang busur CD!
Matematika
Level 8
Geometri
Lingkaran
Diantara titik berikut yang mempunyai jarak 8 satuan terhadap sumbu-y adalah?
Matematika
Level 8
Geometri
Koordinat Kartesius
Pengertian berita adalah ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Unsur-unsur Berita
Read the following teacher’s talk.

Source: shutterstock.com
"Well done, everyone. You did your best in your English speech today. However, some of you still need to speak more confidently."
The comparison form of “more confidently” refers to ….
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Coba perhatikan gambar denah lingkungan komplek Pertama Hijau pada bidang koordinat dua dimensi berikut!

Bagaimanakah posisi rumah Rina terhadap kolam renang?
Matematika
Level 8
Geometri
Koordinat Kartesius
Koordinat Posisi Suatu Benda
Cermati pilihan berikut!
- Tema
- Diksi
- Rasa
- Imaji
- Tipografi
- Amanat
Yang termasuk di dalam struktur lahir sebagai unsur pembangun sebuah puisi adalah nomor ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Pak Anton akan menjual motornya dengan harga Rp3.000.000,00. Motor 135 cc dengan warna kombinasi antara hitam dan putih. Surat lengkap BPKB dan STNK. Pak Anton tinggal di kota Surabaya dan bisa dihubungi di nomor 082234568910.
Manakah iklan baris yang sesuai berdasarkan ilustrasi tersebut?
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Menulis Iklan, Slogan, Poster
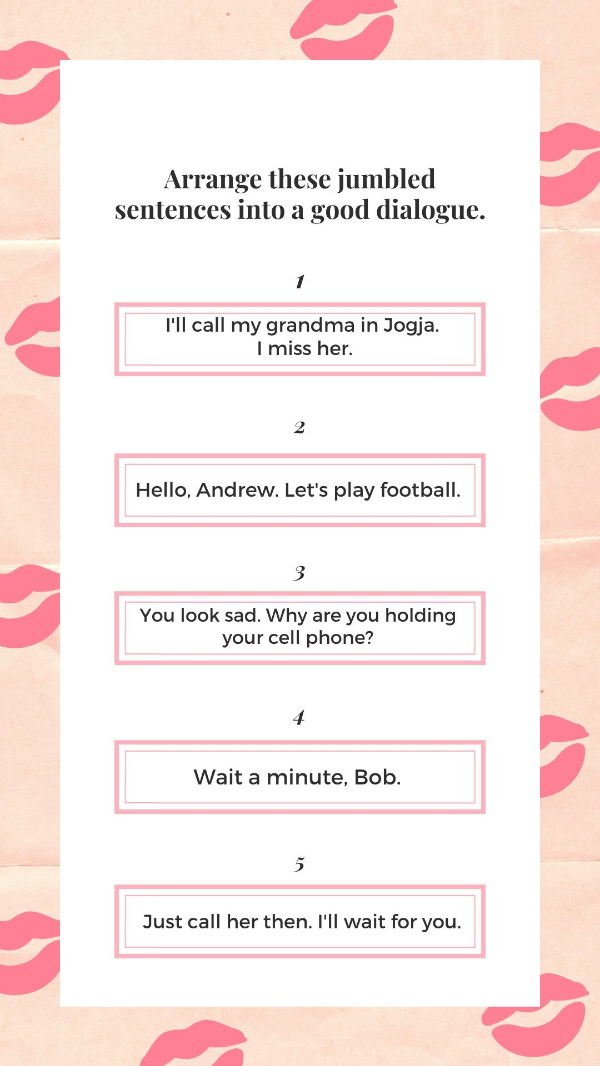
Source: canva.com
What's the best arrangement for the dialogue?
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Willingness to Do Something
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Sebuah dadu dilempar 1 kali. Peluang muncul mata dadu bilangan prima genap adalah...
Jika panjang busur AB adalah 15 cm, maka panjang busur CD adalah ... cm
Perhatikan gambar lingkaran di atas, apabila panjang busur AB = 33 cm dan luas juring COD = 924 cm2, maka tentukanlah panjang busur CD!
Diantara titik berikut yang mempunyai jarak 8 satuan terhadap sumbu-y adalah?
Pengertian berita adalah ....
Read the following teacher’s talk.

Source: shutterstock.com
"Well done, everyone. You did your best in your English speech today. However, some of you still need to speak more confidently."
The comparison form of “more confidently” refers to ….
Coba perhatikan gambar denah lingkungan komplek Pertama Hijau pada bidang koordinat dua dimensi berikut!
Bagaimanakah posisi rumah Rina terhadap kolam renang?
Cermati pilihan berikut!
- Tema
- Diksi
- Rasa
- Imaji
- Tipografi
- Amanat
Yang termasuk di dalam struktur lahir sebagai unsur pembangun sebuah puisi adalah nomor ....
Pak Anton akan menjual motornya dengan harga Rp3.000.000,00. Motor 135 cc dengan warna kombinasi antara hitam dan putih. Surat lengkap BPKB dan STNK. Pak Anton tinggal di kota Surabaya dan bisa dihubungi di nomor 082234568910.
Manakah iklan baris yang sesuai berdasarkan ilustrasi tersebut?
Source: canva.com
What's the best arrangement for the dialogue?



