Bank Soal Matematika SMP Posisi Titik terhadap Titik Tertentu
Soal
LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
1.000 dibaca ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Membilang Sampai 10.000
Perhatikan ilustrasi perubahan zat berikut!

Kata yang tepat untuk mengisi kotak yang kosong adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menyajikan Hasil Informasi
Perhatikan data usia siswa kelas III pada diagram di bawah ini!
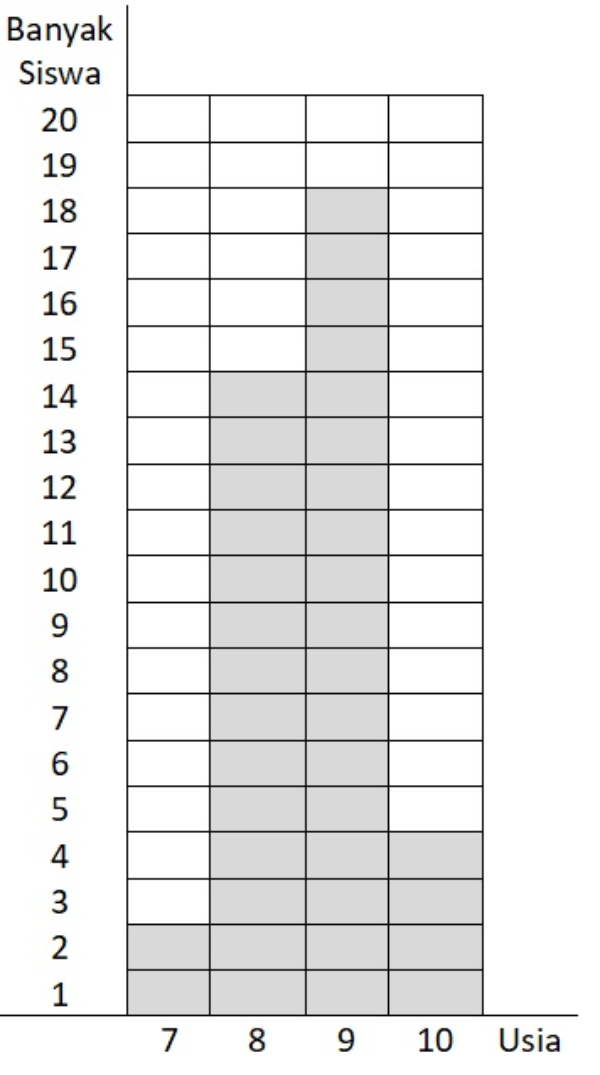
Berapa siswa yang mempunyai usia tertinggi?
Matematika
Level 3
Statistika
Data
Membaca dan Menafsirkan Data
Perhatikan denah berikut!
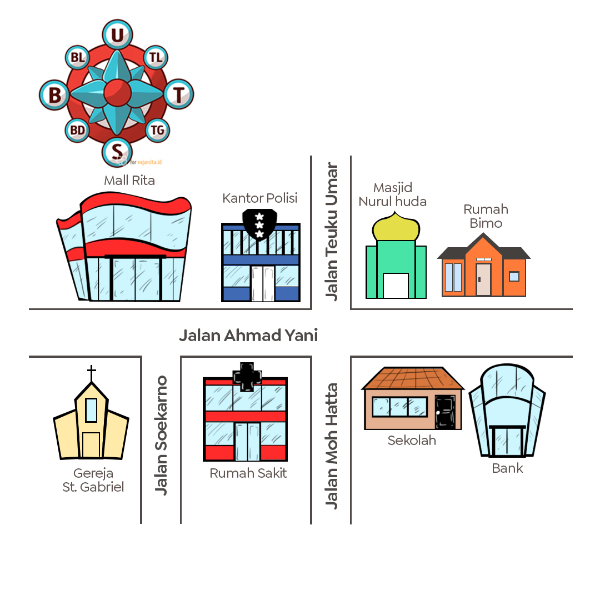
Bangunan yang berada di sebelah barat laut sekolah adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
....
Matematika
Level 3
Bilangan
Pecahan Sederhana
Pengurangan Pecahan Penyebut Sama
Ibu membeli kain sepanjang 520 cm.
Panjang kain yang dibeli ibu dalam satuan m adalah ....
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Hubungan Antarsatuan Panjang
Santi ingin menaruh air dalam termos.
Santi mempunyai 3 termos dengan ukuran berbeda.

(Sumber Gambar: flaticon.com)
Santi memerlukan volume termos yang besar.
Maka, termos yang dipilih Santi adalah ....
Matematika
Level 3
Geometri
Volume Bangun Ruang
Konsep Volume
Perhatikan bangun berikut!
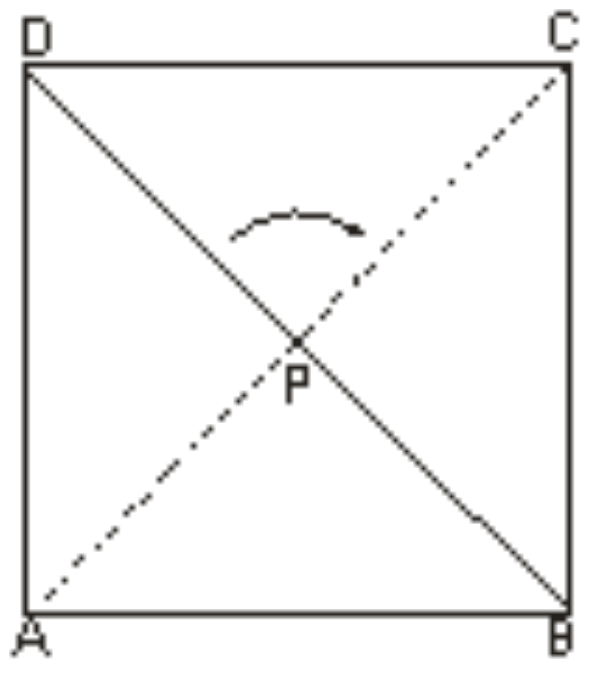
Apabila bangun ABCD diputar 180o searah jarum jam dengan titik P sebagai pusatnya, maka hasil perputaran tersebut adalah ...
Matematika
Level 3
Geometri
Bangun Datar
Simetri dan Pencerminan
Angka yang hilang adalah ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Operasi Hitung Campuran
Perhatikan gambar berikut ini!

Kamu melakukan wawancara dengan orang yang berprofesi seperti gambar di atas. Contoh pertanyaan yang sesuai adalah ...
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menulis Pertanyaan Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
1.000 dibaca ....
Perhatikan ilustrasi perubahan zat berikut!
Kata yang tepat untuk mengisi kotak yang kosong adalah ....
Perhatikan data usia siswa kelas III pada diagram di bawah ini!
Berapa siswa yang mempunyai usia tertinggi?
Perhatikan denah berikut!
Bangunan yang berada di sebelah barat laut sekolah adalah ....
....
Ibu membeli kain sepanjang 520 cm.
Panjang kain yang dibeli ibu dalam satuan m adalah ....
Santi ingin menaruh air dalam termos.
Santi mempunyai 3 termos dengan ukuran berbeda.
(Sumber Gambar: flaticon.com)
Santi memerlukan volume termos yang besar.
Maka, termos yang dipilih Santi adalah ....
Perhatikan bangun berikut!
Apabila bangun ABCD diputar 180o searah jarum jam dengan titik P sebagai pusatnya, maka hasil perputaran tersebut adalah ...
Angka yang hilang adalah ….
Perhatikan gambar berikut ini!
Kamu melakukan wawancara dengan orang yang berprofesi seperti gambar di atas. Contoh pertanyaan yang sesuai adalah ...



