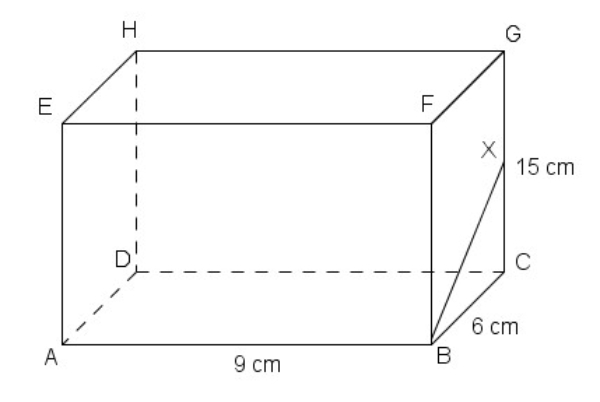
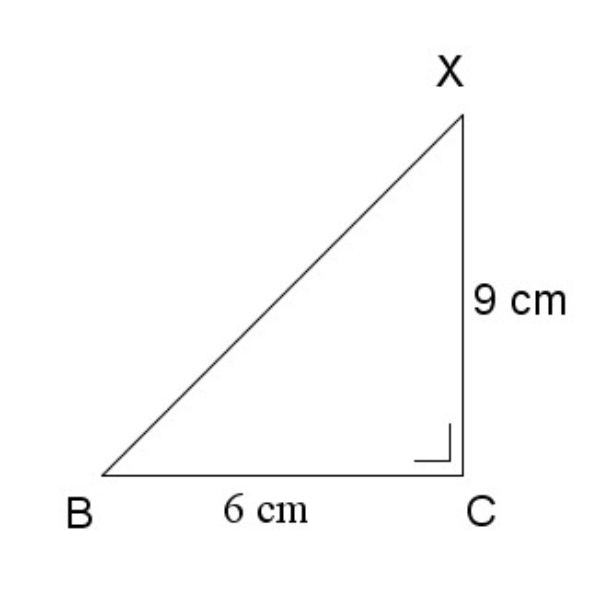
Bank Soal Matematika SMA Sudut pada Bangun Ruang
Soal
Diketahui balok seperti gambar berikut.
Jika titik pada garis dengan , nilai sinus antara garis dan adalah ....
Pembahasan:
Sudut antara garis dan dapat diperoleh dengan memproyeksikan garis ke garis . Proyeksi garis ke garis dapat dilakukan dengan menarik garis dari yang tegak lurus dengan garis
Proyeksi garis ke garis adalah garis . Sehingga sudut antara garis ke garis adalah
.
Perhatikan bahwa:
cm
Dengan mengaplikaikan teorema pythagoras pada diperoleh
cm
Sudut antara garis dan adalah .
Dengan demikian nilai sinus antara garis dan adalah
Rangkuman
Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya
Soal Populer Hari Ini
Frekuensi harapan muncul mata dadu bilangan prima pada pelemparan sebuah dadu adalah 120 kali. Berapa banyak lemparan yang dilakukan?
Matematika
Level 8
Statistika
Peluang
Frekuensi Harapan
Kelas VIII
Kurikulum 2013
K13
Matematika
Panjang busur AB adalah ... cm ( Gunakan = 3,14 )
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
Kelas VIII
Kurikulum 2013
K13
Matematika
Perhatikan gambar berikut!
Jika sudut CDE = 75o, tentukan besar sudut ABC!
Matematika
Level 8
Geometri
Lingkaran
Panjang Busur, Luas Juring dan Tembereng
Kelas VIII
Kurikulum 2013
K13
Matematika
Manakah di antara koordinat titik berikut yang terletak di kuadran IV?
Matematika
Level 8
Geometri
Koordinat Kartesius
Kuadran
Kelas VIII
Kurikulum 2013
K13
Matematika
Read the following comments of a broadway show.
Template/source: canva.com, linetv.com
Which of the following statements is true based on the comments above?
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Urutan struktur teks berita yang benar adalah ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Struktur dan Kebahasaan Teks Berita
KD3.2
Kelas VIII
Kurikulum 2013
K13
Bahasa Indonesia
Cermati puisi berikut!
Aku
Kalau sampai waktuku
‘Ku mau tak seorang ‘kan merayu
Tidak juga kau
Tak perlu sedu sedan itu
Aku ini binatang jalang
Dari kumpulan yang terbuang
Biar peluru menembus kulitku
Aku tetap meradang menerjang
Luka dan bisa kubawa berlari
Berlari
Hingga hilang pedih peri
Dan aku akan lebih tidak peduli
Aku mau hidup seribu tahun lagi!
(Karya: Chairil Anwar)
Citraan yang terdapat pada larik yang dicetak miring tersebut adalah citraan ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
KD3.7
Kelas VIII
Kurikulum 2013
K13
Bahasa Indonesia
Perhatikanlah gambar persegi pada koordinat cartesius berikut.
Manakah diantara titik pada koordinat cartesius yang merupakan titik pusat dari persegi?
Matematika
Level 8
Geometri
Koordinat Kartesius
Posisi Titik dan Bangun Datar
Kelas VIII
Kurikulum 2013
K13
Matematika
Diketahui harga 4 pensil dan 5 buku tulis Rp 19.000, sedangkan harga 3 pensil dan 4 buku tulis Rp 15.000. Jika pensil adalah dan buku tulis adalah , manakah model matematika yang benar?
Matematika
Level 8
Aljabar
Sistem Persamaan Linear Dua Variabel (SPLDV)
Konsep Persamaan Linear Dua Variabel
Kelas VIII
Kurikulum 2013
K13
Matematika
Read the dialogue carefully.
Picture: today.line.me
Rossa : Do you know Tiara Anugrah?
Yoga : Yes. She is a singer, right? She can sing various genres of song very well.
Rossa : Yes. I envy her. Can you sing?
Yoga : Are you joking? Of course I can't. How about you?
Rossa : I can sing particular songs. But I can't perform them well.
Yoga : Why?
Rossa : My voice isn't good enough.
"I can sing particular songs." (Rossa, line 5)
The word particular has similar meaning with ....
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Explaining Abilities
Kelas VIII
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Frekuensi harapan muncul mata dadu bilangan prima pada pelemparan sebuah dadu adalah 120 kali. Berapa banyak lemparan yang dilakukan?
Panjang busur AB adalah ... cm ( Gunakan = 3,14 )
Perhatikan gambar berikut!
Jika sudut CDE = 75o, tentukan besar sudut ABC!
Manakah di antara koordinat titik berikut yang terletak di kuadran IV?
Read the following comments of a broadway show.
Template/source: canva.com, linetv.com
Which of the following statements is true based on the comments above?
Urutan struktur teks berita yang benar adalah ....
Cermati puisi berikut!
Aku
Kalau sampai waktuku
‘Ku mau tak seorang ‘kan merayu
Tidak juga kau
Tak perlu sedu sedan itu
Aku ini binatang jalang
Dari kumpulan yang terbuang
Biar peluru menembus kulitku
Aku tetap meradang menerjang
Luka dan bisa kubawa berlari
Berlari
Hingga hilang pedih peri
Dan aku akan lebih tidak peduli
Aku mau hidup seribu tahun lagi!
(Karya: Chairil Anwar)
Citraan yang terdapat pada larik yang dicetak miring tersebut adalah citraan ....
Perhatikanlah gambar persegi pada koordinat cartesius berikut.
Manakah diantara titik pada koordinat cartesius yang merupakan titik pusat dari persegi?
Diketahui harga 4 pensil dan 5 buku tulis Rp 19.000, sedangkan harga 3 pensil dan 4 buku tulis Rp 15.000. Jika pensil adalah dan buku tulis adalah , manakah model matematika yang benar?
Read the dialogue carefully.
Picture: today.line.me
Rossa : Do you know Tiara Anugrah? Yoga : Yes. She is a singer, right? She can sing various genres of song very well. Rossa : Yes. I envy her. Can you sing? Yoga : Are you joking? Of course I can't. How about you? Rossa : I can sing particular songs. But I can't perform them well. Yoga : Why? Rossa : My voice isn't good enough.
"I can sing particular songs." (Rossa, line 5)
The word particular has similar meaning with ....
