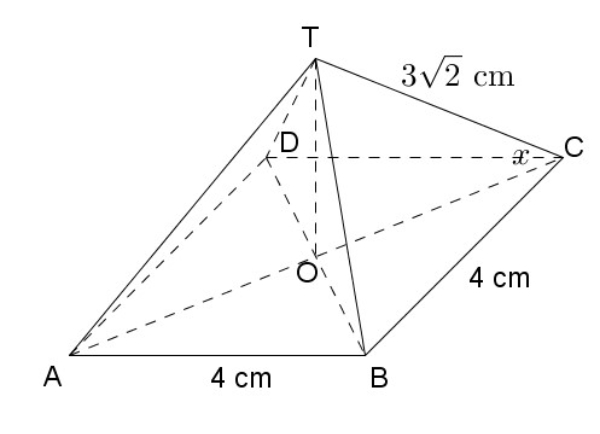
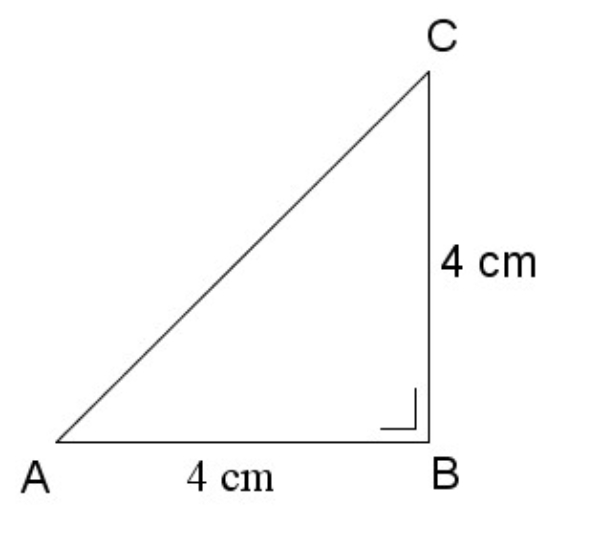
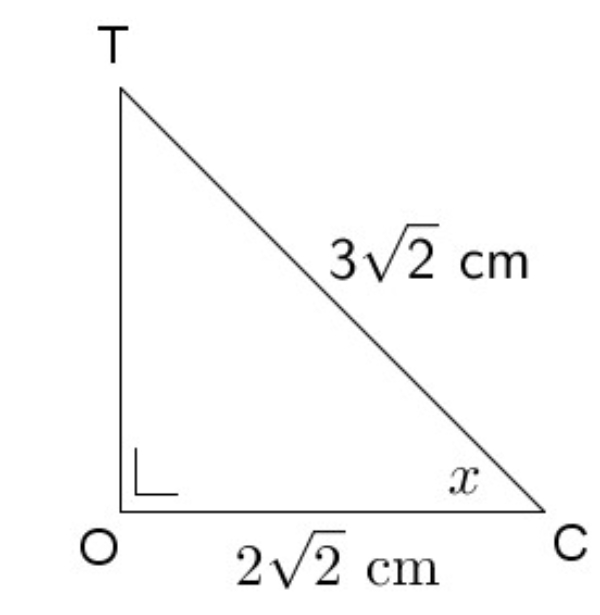
Bank Soal Matematika SMA Sudut pada Bangun Ruang
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Jenis polisakarida yang terdapat pada sel otot dan hati hewan serta berperan sebagai cadangan makanan adalah ....
Biologi
Level 11
Biologi
Sel
Penemuan, Tipe, Ukuran, dan Komponen Kimiawi Sel
Kelas XI
Kurikulum 2013
K13
Jika garis digeser ke atas sejauh 2 satuan dan ke kanan sejauh 6 satuan, maka bayangan yang terbentuk adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
Kelas XI
Kurikulum 2013
K13
Matematika Wajib
Choose the right offer for the following situation.

You look at your friend in front of his apartment. He can’t move the heavy boxes.
Bahasa Inggris
Level 11
Good Advice
Making Offers
Kelas XI
Kurikulum 2013
K13
Bahasa Inggris
Deret dapat ditulis dalam notasi sigma menjadi ....
Matematika
Level 11
Logika
Induksi Matematika
Notasi Sigma
Kelas XI
Kurikulum 2013
K13
Matematika Wajib
Berikut ini yang bukan merupakan benda yang mengandung senyawa hidrokarbon adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Kelas XI
Kurikulum 2013
K13
Kimia

Sebuah helikopter memiliki 3 bilah baling-baling yang memiliki massa 20 kg dengan jari-jari 3 m. Baling-baling ini diputar dengan kecepatan sudut 100 rad/s. Momentum sudut yang dimiliki baling-baling ini adalah ... kg m2/s. (momen inersia baling-baling helikopter dengan 3 bilah )
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Dinamika Benda Tegar
Kelas XI
Kurikulum 2013
K13
Perhatikan data di bawah ini!
- Ukuran partikel
- Luas area
- Suhu
- Jarak
Berdasarkan data di atas, faktor-faktor yang mempengaruhi kecepatan difusi adalah nomor ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Kelas XI
Kurikulum 2013
K13
Di antara senyawa hidrokarbon berikut yang merupakan senyawa golongan alkana adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Kelas XI
Kurikulum 2013
K13
Kimia
Terdapat sebuah persamaan trigonometri , maka salah satu nilai dari dapat didefinisikan sebagai ....
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Kelas XI
Kurikulum 2013
K13
Matematika Peminatan
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
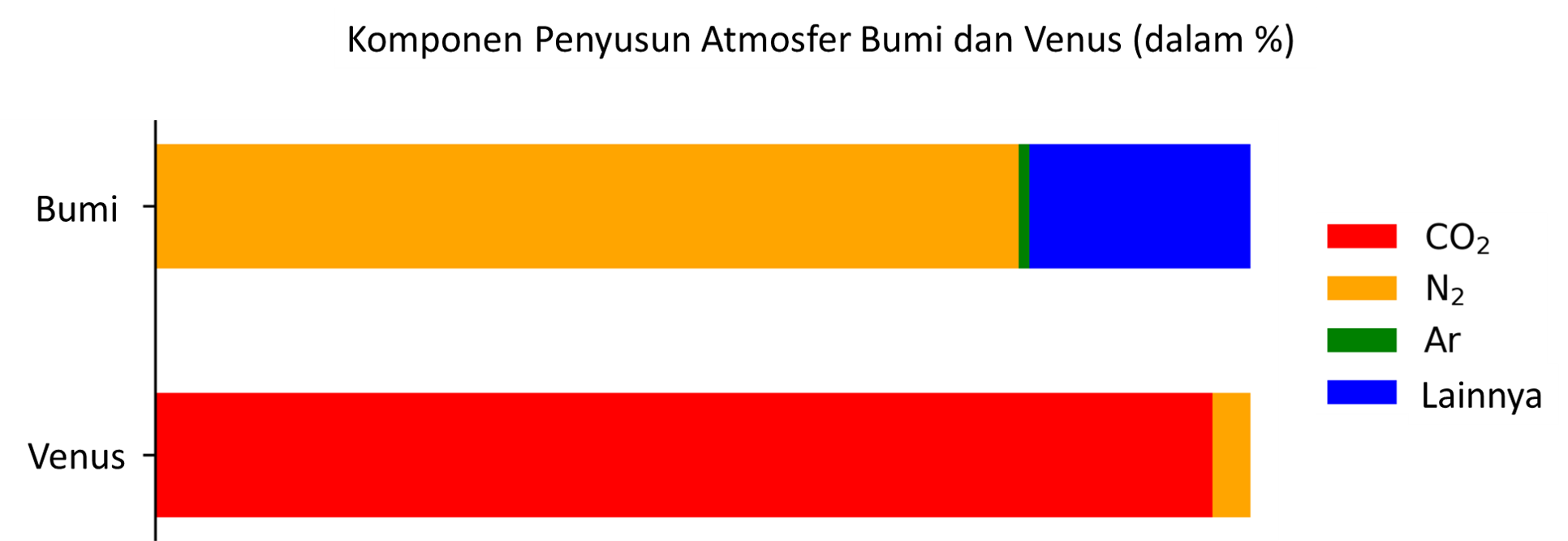
Berdasarkan data tersebut, kemungkinan efek rumah kaca terjadi lebih besar di ... dan planet yang memiliki suhu permukaan rata-rata yang lebih rendah adalah ....
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Kelas XI
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Jenis polisakarida yang terdapat pada sel otot dan hati hewan serta berperan sebagai cadangan makanan adalah ....
Jika garis digeser ke atas sejauh 2 satuan dan ke kanan sejauh 6 satuan, maka bayangan yang terbentuk adalah ....
Choose the right offer for the following situation.

You look at your friend in front of his apartment. He can’t move the heavy boxes.
Deret dapat ditulis dalam notasi sigma menjadi ....
Berikut ini yang bukan merupakan benda yang mengandung senyawa hidrokarbon adalah ....

Sebuah helikopter memiliki 3 bilah baling-baling yang memiliki massa 20 kg dengan jari-jari 3 m. Baling-baling ini diputar dengan kecepatan sudut 100 rad/s. Momentum sudut yang dimiliki baling-baling ini adalah ... kg m2/s. (momen inersia baling-baling helikopter dengan 3 bilah )
Perhatikan data di bawah ini!
- Ukuran partikel
- Luas area
- Suhu
- Jarak
Berdasarkan data di atas, faktor-faktor yang mempengaruhi kecepatan difusi adalah nomor ....
Di antara senyawa hidrokarbon berikut yang merupakan senyawa golongan alkana adalah ....
Terdapat sebuah persamaan trigonometri , maka salah satu nilai dari dapat didefinisikan sebagai ....
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
Berdasarkan data tersebut, kemungkinan efek rumah kaca terjadi lebih besar di ... dan planet yang memiliki suhu permukaan rata-rata yang lebih rendah adalah ....