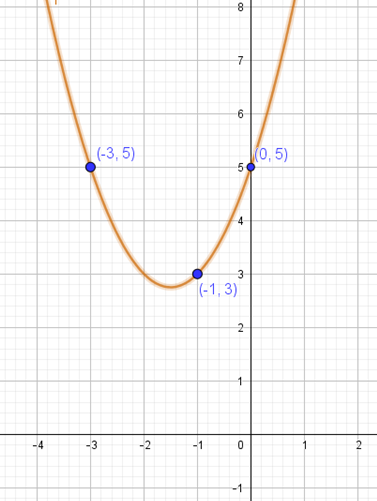
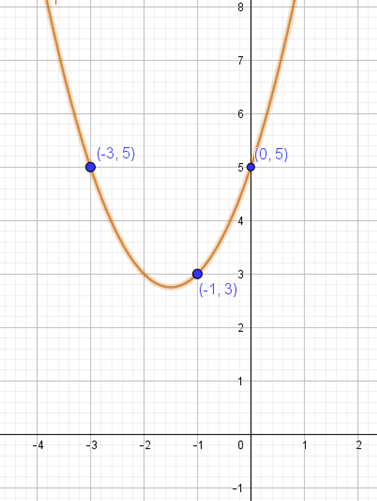
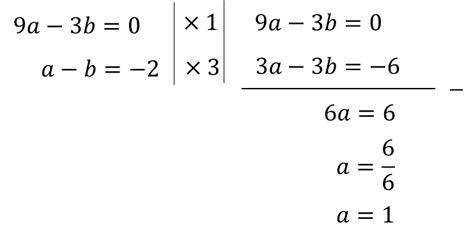Bank Soal Matematika SMP Menyusun Persamaan Kuadrat
Soal
Teknik Hitung LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bilangan 73 ... 102
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Membandingkan dan Mengurutkan Bilangan
Maaf, Tina. Aku tidak bisa ikut bermain bersama karena harus pergi bersama Ibu.
Ungkapan penolakan tersebut diucapkan seseorang untuk ....
Bahasa Indonesia
Level 2
Menulis
Ungkapan (1)
Ungkapan Penolakan
Gambar yang tepat untuk melanjutkan pola barisan berikut ini adalah ....

(Sumber: freepik.com)
Matematika
Level 2
Geometri
Bangun Ruang sederhana
Pola Barisan Bangun Ruang
Lala menemukan uang di laci dengan uang seperti berikut.



(Sumber Gambar: DocPlayer.info)
Jenis uang yang ditemukan Lala adalah uang ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Macam-Macam Jenis Uang
Perhatikan gambar berikut!

(Sumber Gambar: freepik.com)
Gambar yang tepat untuk melanjutkan pola barisan di atas adalah ....
Matematika
Level 2
Geometri
Bangun Datar Sederhana
Pola Barisan Bangun Datar
Asa pergi ke toko.
Di toko tersebut menjual berbagai macam alat tulis.
Berikut adalah daftar harga berbagai macam alat tulis yang dijual.

(Sumber Gambar: flaticon.com)
Asa memiliki 1 lembar uang dua ribuan.
Ia ingin menggunakan uangnya untuk membeli 2 jenis barang tetapi masih mendapatkan uang kembalian.
Barang yang dapat dibeli Asa adalah ....
Matematika
Level 2
Bilangan
Nilai dan Kesetaraan Mata Uang
Kesetaraan Nilai Mata Uang
Fill in the blanks.
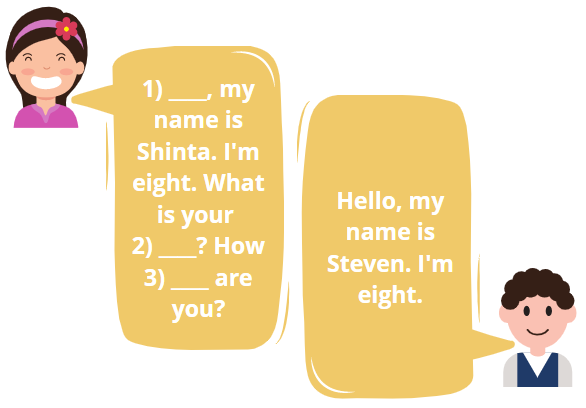
Number 3 is ______.
Bahasa Inggris
Level 2
A NEW FRIEND
Greetings and Spelling
Manakah yang disebut jam analog?
Matematika
Level 2
Bilangan
Satuan Waktu, Panjang, dan Berat
Mengenal Alat Ukur Waktu
Perhatikan puisi berikut.
Terjatuh
Aku terjatuh saat berlari
Lututku berdarah
Perih terasa
Aku sangat sedih
karena tidak bisa bermain
tidak bisa kejar-kejaran
Ekspresi yang sesuai dengan puisi tersebut adalah ….
Bahasa Indonesia
Level 2
Membaca
Puisi Anak
Lafal, Intonasi, dan Ekspresi dalam Membaca Puisi
Terdapat dua buah bilangan.
Kedua bilangan memiliki nilai ratusan yang sama.
Tetapi bilangan pertama memiliki nilai puluhan yang lebih besar dari bilangan kedua.
Sebaliknya, nilai satuan pada bilangan kedua lebih besar dari bilangan pertama.
Bilangan pertama dan kedua berturut-turut yang sesuai adalah ....
Matematika
Level 2
Bilangan
Mengenal Bilangan Cacah (0-999)
Menentukan Nilai Tempat Bilangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bilangan 73 ... 102
Maaf, Tina. Aku tidak bisa ikut bermain bersama karena harus pergi bersama Ibu.
Ungkapan penolakan tersebut diucapkan seseorang untuk ....
Gambar yang tepat untuk melanjutkan pola barisan berikut ini adalah ....
(Sumber: freepik.com)
Lala menemukan uang di laci dengan uang seperti berikut.
(Sumber Gambar: DocPlayer.info)
Jenis uang yang ditemukan Lala adalah uang ....
Perhatikan gambar berikut!
(Sumber Gambar: freepik.com)
Gambar yang tepat untuk melanjutkan pola barisan di atas adalah ....
Asa pergi ke toko.
Di toko tersebut menjual berbagai macam alat tulis.
Berikut adalah daftar harga berbagai macam alat tulis yang dijual.
(Sumber Gambar: flaticon.com)
Asa memiliki 1 lembar uang dua ribuan.
Ia ingin menggunakan uangnya untuk membeli 2 jenis barang tetapi masih mendapatkan uang kembalian.
Barang yang dapat dibeli Asa adalah ....
Fill in the blanks.
Number 3 is ______.
Manakah yang disebut jam analog?
Perhatikan puisi berikut.
Terjatuh
Aku terjatuh saat berlari
Lututku berdarah
Perih terasa
Aku sangat sedih
karena tidak bisa bermain
tidak bisa kejar-kejaran
Ekspresi yang sesuai dengan puisi tersebut adalah ….
Terdapat dua buah bilangan.
Kedua bilangan memiliki nilai ratusan yang sama.
Tetapi bilangan pertama memiliki nilai puluhan yang lebih besar dari bilangan kedua.
Sebaliknya, nilai satuan pada bilangan kedua lebih besar dari bilangan pertama.
Bilangan pertama dan kedua berturut-turut yang sesuai adalah ....