Bank Soal Matematika SMA Barisan Geometri
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Sebuah dadu dilempar 1 kali. Peluang muncul mata dadu bilangan prima genap adalah...
Matematika
Level 8
Statistika
Peluang
Berikut manakah yang merupakan rumus mencari luas lingkaran?
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
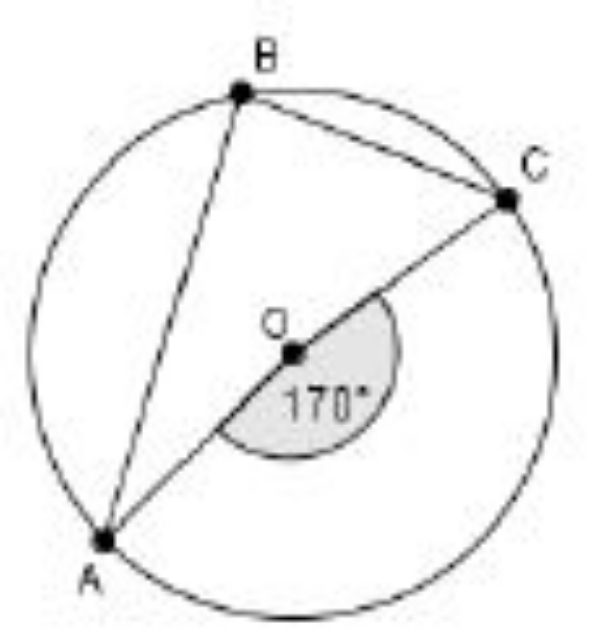
Tentukanlah besar sudut keliling ABC jika besar sudut AOC = 170o!
Matematika
Level 8
Geometri
Lingkaran
Sebuah belah ketupat KLMN mempunyai koordinat titik tengah (3, 3) dan titik K(3, 7). Berapakah koordinat titik M?
Matematika
Level 8
Geometri
Koordinat Kartesius
Urutan struktur teks berita yang benar adalah ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Struktur dan Kebahasaan Teks Berita
Bella — shop — frequent — Nia
Which comparative sentence is correct based on the clues above?
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Jika titik dan , maka koordinat posisi titik terhadap titik adalah ....
Matematika
Level 8
Geometri
Koordinat Kartesius
Koordinat Posisi Suatu Benda
Perbedaan makna konotasi dan makna denotasi dalam puisi adalah ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Perhatikan data berikut!
1) Sebagai media promosi.
2) Menjelaskan suatu produk atau jasa.
3) Sebagai pengingat.
4) Dorongan melakukan tindakan.
5) Pesan bersifat informatif.
6) Kata-kata yang digunakan menarik.
Ciri-ciri iklan ditunjukkan nomor ....
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Unsur-unsur Iklan, Slogan, Poster
You are about going to the bookstore to buy some novels. Suddenly, you meet your classmate on the way you go to the bookstore. You want to ask him whether he is willing to come with you to the bookstore or not. You may say ....
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Willingness to Do Something
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Sebuah dadu dilempar 1 kali. Peluang muncul mata dadu bilangan prima genap adalah...
Berikut manakah yang merupakan rumus mencari luas lingkaran?
Tentukanlah besar sudut keliling ABC jika besar sudut AOC = 170o!
Sebuah belah ketupat KLMN mempunyai koordinat titik tengah (3, 3) dan titik K(3, 7). Berapakah koordinat titik M?
Urutan struktur teks berita yang benar adalah ....
Bella — shop — frequent — Nia
Which comparative sentence is correct based on the clues above?
Jika titik dan , maka koordinat posisi titik terhadap titik adalah ....
Perbedaan makna konotasi dan makna denotasi dalam puisi adalah ....
Perhatikan data berikut!
1) Sebagai media promosi.
2) Menjelaskan suatu produk atau jasa.
3) Sebagai pengingat.
4) Dorongan melakukan tindakan.
5) Pesan bersifat informatif.
6) Kata-kata yang digunakan menarik.
Ciri-ciri iklan ditunjukkan nomor ....
You are about going to the bookstore to buy some novels. Suddenly, you meet your classmate on the way you go to the bookstore. You want to ask him whether he is willing to come with you to the bookstore or not. You may say ....



