Bank Soal Matematika SMA Deret Aritmetika
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Iklan di radio termasuk jenis iklan media elektronik berupa iklan ….
Bahasa Indonesia
Level 5
Membaca
Iklan
Jenis-jenis Iklan
Sebuah bak mandi terisi air sebanyak 1.500 liter. Agar bak tersebut dapat terisi 2 m3 air, maka volume bak harus ditambah sebanyak … m3.
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Debit
Read the following dialogue and answer the question.

Mom: Son, this is our new neighbor, Jenny.
Aiden: Hey, Jenny.
Jenny: Hello. What is your name?
Aiden: I'm Aiden.
Jenny: Can you spell it?
Aiden: ….
Which spelling is correct to complete the dialogue?
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Spelling
Bagian tanah yang mencapai tinggi 600 meter di atas permukaan laut dan menyerupai kerucut disebut ....
IPS
Level 5
Geografi
Karakteristik Geografi Wilayah Indonesia
Kondisi Wilayah Indonesia
Perhatikan gambar berikut!
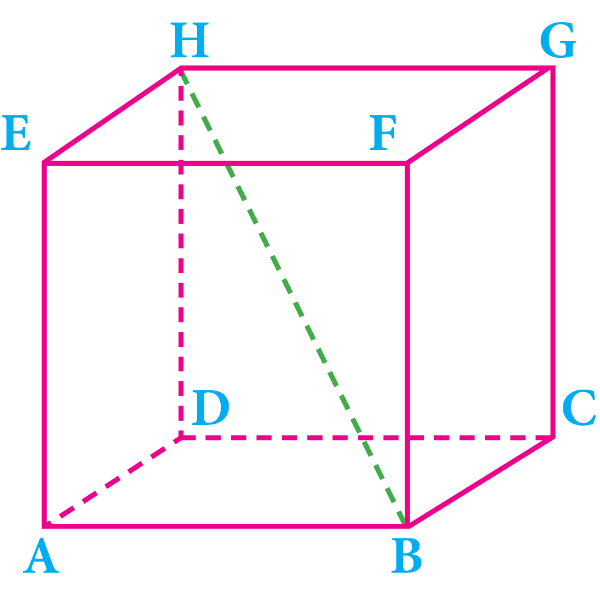
Garis hijau yang menghubungkan titik B dengan tittik H pada gambar kubus di atas disebut ....
Matematika
Level 5
Geometri
Balok dan Kubus
Sifat dan Jaring-Jaring Balok dan Kubus
Andi menjadi penjaga perpustakaan. Ia wajib mencatat jumlah pengunjung dalam seminggu. Berikut catatan milik Andi.
Senin = 50 pengunjung / Selasa = 100 pengunjung / Rabu = 75 pengunjung / Kamis = 100 pengunjung / Minggu = 125 pengunjung
Andi lupa mencatat jumlah pengunjung di hari Jumat dan Sabtu. Ia hanya ingat pada hari Jumat jumlah pengunjung mengalami kenaikan sebanyak 50 pengunjung dari hari sebelumnya. Sedangkan pada hari Minggu jumlah pengunjung mengalami penurunan sebanyak 25 pengunjung dari hari sebelumnya.
Tentukan tabel di bawah ini yang tepat sesuai cerita di atas!
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Menyajikan Data
Diketahui data tinggi badan (dalam cm) dari 30 murid kelas VI sebagai berikut.

Berapa cm tinggi badan terendah? Ada berapa orang yang memiliki tinggi badan terendah?
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Bacalah teks berikut!
Pedoman gizi seimbang kini telah diimplementasikan di Indonesia sebagai upaya realisasi dan rekomendasi Konferensi Pangan Sedunia di Roma tahun 1992. Pedoman tersebut menggantikan slogan "4 sehat 5 sempurna" yang telah diperkenalkan sejak tahun 1952 karena sudah tidak sesuai lagi dengan perkembangan ilmu pengetahuan dan teknologi (IPTEK) dalam bidang gizi.
Hal yang diperhatikan dalam pedoman gizi seimbang yaitu variasi makanan, pentingnya pola hidup bersih, pentingnya pola hidup aktif dan olahraga, serta memantau berat badan ideal. Dalam gambaran Tumpeng Gizi Seimbang (TGS) setiap orang dianjurkan untuk minum air putih rata-rata 8 gelas setiap harinya. Hal ini karena air merupakan bagian zat yang penting bagi kelangsungan hidup. Berikutnya disusul oleh karbohidrat yang dianjurkan untuk dikonsumsi 3-8 porsi (sesuai kebutuhan menurut usia, berat badan, dan keadaan kesehatan). Lalu sayur dan buah sebagai sumber serat, vitamin, dan mineral. Selain itu, sayuran harus lebih banyak dikonsumsi daripada buah. Kemudian, protein hewani dan nabati dikonsumsi lebih sedikit daripada sayuran dan buah. Paling puncak dilengkapi oleh minyak, gula, dan garam yang bisa digunakan seperlunya.
Judul yang tepat untuk teks eksplanasi tersebut adalah ....
Bahasa Indonesia
Level 5
Membaca
Teks Eksplanasi
Menulis Teks Eksplanasi
Cermati contoh surat berikut ini.

Tujuan Dinas Kebudayaan Kota Cirebon mengadakan lomba Melukis dari Rumah adalah ....
Bahasa Indonesia
Level 5
Membaca
Surat Undangan
Identifikasi Surat Undangan
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Iklan di radio termasuk jenis iklan media elektronik berupa iklan ….
Sebuah bak mandi terisi air sebanyak 1.500 liter. Agar bak tersebut dapat terisi 2 m3 air, maka volume bak harus ditambah sebanyak … m3.
Read the following dialogue and answer the question.

Mom: Son, this is our new neighbor, Jenny.
Aiden: Hey, Jenny.
Jenny: Hello. What is your name?
Aiden: I'm Aiden.
Jenny: Can you spell it?
Aiden: ….
Which spelling is correct to complete the dialogue?
Bagian tanah yang mencapai tinggi 600 meter di atas permukaan laut dan menyerupai kerucut disebut ....
Perhatikan gambar berikut!
Garis hijau yang menghubungkan titik B dengan tittik H pada gambar kubus di atas disebut ....
Andi menjadi penjaga perpustakaan. Ia wajib mencatat jumlah pengunjung dalam seminggu. Berikut catatan milik Andi.
Senin = 50 pengunjung / Selasa = 100 pengunjung / Rabu = 75 pengunjung / Kamis = 100 pengunjung / Minggu = 125 pengunjung
Andi lupa mencatat jumlah pengunjung di hari Jumat dan Sabtu. Ia hanya ingat pada hari Jumat jumlah pengunjung mengalami kenaikan sebanyak 50 pengunjung dari hari sebelumnya. Sedangkan pada hari Minggu jumlah pengunjung mengalami penurunan sebanyak 25 pengunjung dari hari sebelumnya.
Tentukan tabel di bawah ini yang tepat sesuai cerita di atas!
Diketahui data tinggi badan (dalam cm) dari 30 murid kelas VI sebagai berikut.
Berapa cm tinggi badan terendah? Ada berapa orang yang memiliki tinggi badan terendah?
Bacalah teks berikut!
Pedoman gizi seimbang kini telah diimplementasikan di Indonesia sebagai upaya realisasi dan rekomendasi Konferensi Pangan Sedunia di Roma tahun 1992. Pedoman tersebut menggantikan slogan "4 sehat 5 sempurna" yang telah diperkenalkan sejak tahun 1952 karena sudah tidak sesuai lagi dengan perkembangan ilmu pengetahuan dan teknologi (IPTEK) dalam bidang gizi.
Hal yang diperhatikan dalam pedoman gizi seimbang yaitu variasi makanan, pentingnya pola hidup bersih, pentingnya pola hidup aktif dan olahraga, serta memantau berat badan ideal. Dalam gambaran Tumpeng Gizi Seimbang (TGS) setiap orang dianjurkan untuk minum air putih rata-rata 8 gelas setiap harinya. Hal ini karena air merupakan bagian zat yang penting bagi kelangsungan hidup. Berikutnya disusul oleh karbohidrat yang dianjurkan untuk dikonsumsi 3-8 porsi (sesuai kebutuhan menurut usia, berat badan, dan keadaan kesehatan). Lalu sayur dan buah sebagai sumber serat, vitamin, dan mineral. Selain itu, sayuran harus lebih banyak dikonsumsi daripada buah. Kemudian, protein hewani dan nabati dikonsumsi lebih sedikit daripada sayuran dan buah. Paling puncak dilengkapi oleh minyak, gula, dan garam yang bisa digunakan seperlunya.
Judul yang tepat untuk teks eksplanasi tersebut adalah ....
Cermati contoh surat berikut ini.
Tujuan Dinas Kebudayaan Kota Cirebon mengadakan lomba Melukis dari Rumah adalah ....



