Bank Soal Matematika SMA Konsep dan Sifat-Sifat Limit Fungsi
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
The text below is for the following question.

picture: lifewire.com
If you are a junior high school student, you'll start to use email when submitting your tasks to your teachers. Have you tried it before? Read the way how to do it below. Make sure you already have an email account first. You can create your account using some providers such as Gmail or Yahoo.
First, open your email account. Let's use Gmail as an example.
Second, after the window is opened, look at the left side of your window. There is a white circle icon with a plus in it and the word 'compose'. Click it, and a form for email will appear.
Third, write the receiver's email address. Make sure the address is correct, or your email will not be sent. Also, write the subject of your email. If it's a task, you can write the name of the subject and what the task is about.
Next, write your message/task in the box provided. Open with introduction or greeting. You can also attach documents if your task is written in Microsoft Word. Just click the 'attach files' icon, choose your files, and click 'select'. Your documents will be attached to your email.
Do not forget to write the closing for your email. If you have finished writing the contents of your email, click 'send' and your email will be sent to your teacher.
Good luck!
The text above is intended to ....
Bahasa Inggris
Level 9
Bahasa Inggris
How to do or make things
Procedure Text
Observe the classroom reward chart below and answer the question.

Source: canva.com
Which of the following information is NOT stated on the chart?
Bahasa Inggris
Level 9
Bahasa Inggris
Using passive voice to describe things
Passive Voice
Penelitian ini bertujuan untuk mengetahui kadar vitamin C pada bagian tanaman jeruk (daun, kulit, buah).
Berdasarkan tujuan penelitian tersebut, objek penelitiannya adalah ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Identifikasi Laporan Percobaan
Penjabaran yang benar dari adalah ...
Matematika
Level 9
Bilangan
Bilangan Berpangkat dan Bentuk Akar
Bilangan Berpangkat
Bagian teks diskusi yang berisi penyampaian argumen dari kelompok pro dan kontra adalah ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Struktur dan Kebahasaan Teks Diskusi
Perhatikan tabel dalam kutipan teks laporan percobaan berikut dengan saksama!
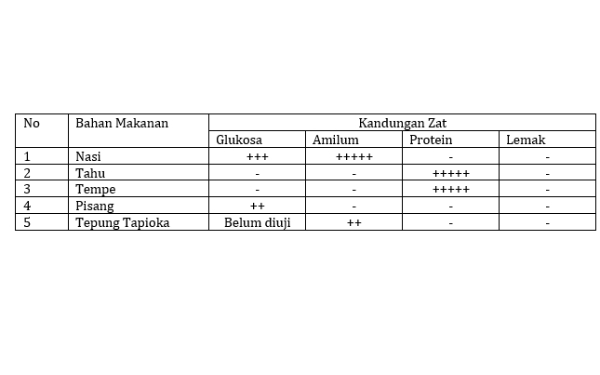
(Sumber: academia.edu-Laporan Uji Zat Makanan)
Tabel tersebut digunakan untuk menyajikan data pada bagian ....
Bahasa Indonesia
Level 9
Menulis
Laporan Percobaan
Identifikasi Laporan Percobaan
Read the following letter and answer the question.

Template: canva.com
Which of the following words has synonyms with the words used in paragraph 2?
Bahasa Inggris
Level 9
Bahasa Inggris
Appreciation over achievements or happiness
Expressions of Congratulations
Baca teks berikut dengan cermat.
Dampak positif memilih kelinci sebagai hewan peliharaan anak, di antaranya, adalah
- kelinci tidak memerlukan ruangan yang luas dan lebih nyaman berada di dalam kandang;
- kelinci adalah hewan yang mampu menyayangi dan biasanya memiliki bulu serta tubuh yang bersih;
- kelinci merupakan hewan yang mudah dilatih menjadi penurut, seperti buang air di tempatnya;
- umumnya orang-orang yang alergi pada kucing dan anjing tidak memiliki kondisi serupa pada kelinci;
- suara kelinci tidak menimbulkan kebisingan; serta
- kelinci merupakan hewan yang penurut dan tidak agresif sehingga bisa menjadi teman dekat bagi anak untuk menumbuhkan rasa kasih sayang anak.
(Sumber: Kompas.com, dengan penyesuaian)
Teks di atas merupakan bagian dari isi teks diskusi, yaitu ....
Bahasa Indonesia
Level 9
Menulis
Teks Diskusi
Struktur dan Kebahasaan Teks Diskusi
- Mencatat nilai-nilai pelajaran yang dapat dipetik di dalam cerita
- Memahami isi cerita
- Membaca keseluruhan cerita dengan cermat
- Menentukan garis besar dan merumuskan simpulan teks
Urutan langkah-langkah menyimpulkan teks inspiratif yang benar adalah ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Menulis Cerita Inspiratif
Baca teks berikut ini dengan cermat.
Melisa, Siswa SD Berprestasi Meski Menulis Hanya Menggunakan Kaki
Melisa Diana Putri adalah seorang siswi difabel di SDN Tukul II Kecamatan Sumber, Kabupaten Probolinggo, Jawa Timur. Melisa duduk di kelas 8. Ia bercita-cita menjadi guru. Semangatnya sangat tinggi meski ia belajar dan beraktivitas menggunakan kaki.
Melisa mengikuti pelajaran di sekolah bersama teman-temannya seperti biasa. Namun saat menulis di buku tulis, dia menggunakan jari kaki. Oleh sekolah, meja khusus dia menulis dibuat lebih rendah dari tubuhnya. Saat menulis di papan tulis untuk mengerjakan tugas dari guru, ia juga menggunakan kaki. Kaki kirinya menopang tubuh agar seimbang, sementara kaki kanannya lincah menulis di papan tulis. Meski menggunakan kaki sejak lahir, tulisan Melisa rapi.
Meskipun memiliki keterbatasan fisik, Melisa sangat tekun dalam belajar. Ia sangat bersemangat meraih prestasi dan nilai baik. Menurut pengakuan gurunya, Melisa memang sangat jago matematika. Selain itu, Melisa juga hobi membaca. Buku apa pun dia baca. Melisa mengaku, ia membaca buku untuk memperluas wawasan.
Menurut Tri Adi Nurfeni, guru Bahasa Indonesia, Melisa meraih cukup banyak prestasi. Melisa pernah juara lomba baca, tulis dan hitung tingkat kecamatan, dan ditunjuk menjadi duta sekolah karena pengetahuannya yang bagus. Berkat pencapaian Melisa, Wakil Bupati Timbul Prihanjoko mengunjungi Melisa di sekolah. Joko, panggilan akrab Wakil Bupati Probolinggi, terharu melihat semangat Melisa untuk meraih cita-cita. Joko dan sejumlah pejabat Pemkab Probolinggo memberi sejumlah bantuan untuk kelanjutan belajar Melisa.
Melisa menjadi bukti bahwa keterbatasan fisik tidak menghalangi seseorang dalam meraih prestasi. Berkat ketekunan dalam belajar, Melisa dapat menghilangkan keterbatasan-keterbatasan itu tadi.
(Sumber: Kompas.com, dengan penyesuaian)
Paragraf yang berisi bagian resolusi adalah ....
Bahasa Indonesia
Level 9
Menulis
Cerita Inspiratif
Struktur dan Kaidah Kebahasaan Teks Cerita Inspiratif
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
The text below is for the following question.
picture: lifewire.com
If you are a junior high school student, you'll start to use email when submitting your tasks to your teachers. Have you tried it before? Read the way how to do it below. Make sure you already have an email account first. You can create your account using some providers such as Gmail or Yahoo.
First, open your email account. Let's use Gmail as an example.
Second, after the window is opened, look at the left side of your window. There is a white circle icon with a plus in it and the word 'compose'. Click it, and a form for email will appear.
Third, write the receiver's email address. Make sure the address is correct, or your email will not be sent. Also, write the subject of your email. If it's a task, you can write the name of the subject and what the task is about.
Next, write your message/task in the box provided. Open with introduction or greeting. You can also attach documents if your task is written in Microsoft Word. Just click the 'attach files' icon, choose your files, and click 'select'. Your documents will be attached to your email.
Do not forget to write the closing for your email. If you have finished writing the contents of your email, click 'send' and your email will be sent to your teacher.
Good luck!
The text above is intended to ....
Observe the classroom reward chart below and answer the question.
Source: canva.com
Which of the following information is NOT stated on the chart?
Penelitian ini bertujuan untuk mengetahui kadar vitamin C pada bagian tanaman jeruk (daun, kulit, buah).
Berdasarkan tujuan penelitian tersebut, objek penelitiannya adalah ....
Penjabaran yang benar dari adalah ...
Bagian teks diskusi yang berisi penyampaian argumen dari kelompok pro dan kontra adalah ....
Perhatikan tabel dalam kutipan teks laporan percobaan berikut dengan saksama!
(Sumber: academia.edu-Laporan Uji Zat Makanan)
Tabel tersebut digunakan untuk menyajikan data pada bagian ....
Read the following letter and answer the question.
Template: canva.com
Which of the following words has synonyms with the words used in paragraph 2?
Baca teks berikut dengan cermat.
Dampak positif memilih kelinci sebagai hewan peliharaan anak, di antaranya, adalah
- kelinci tidak memerlukan ruangan yang luas dan lebih nyaman berada di dalam kandang;
- kelinci adalah hewan yang mampu menyayangi dan biasanya memiliki bulu serta tubuh yang bersih;
- kelinci merupakan hewan yang mudah dilatih menjadi penurut, seperti buang air di tempatnya;
- umumnya orang-orang yang alergi pada kucing dan anjing tidak memiliki kondisi serupa pada kelinci;
- suara kelinci tidak menimbulkan kebisingan; serta
- kelinci merupakan hewan yang penurut dan tidak agresif sehingga bisa menjadi teman dekat bagi anak untuk menumbuhkan rasa kasih sayang anak.
(Sumber: Kompas.com, dengan penyesuaian)
Teks di atas merupakan bagian dari isi teks diskusi, yaitu ....
- Mencatat nilai-nilai pelajaran yang dapat dipetik di dalam cerita
- Memahami isi cerita
- Membaca keseluruhan cerita dengan cermat
- Menentukan garis besar dan merumuskan simpulan teks
Urutan langkah-langkah menyimpulkan teks inspiratif yang benar adalah ....
Baca teks berikut ini dengan cermat.
Melisa, Siswa SD Berprestasi Meski Menulis Hanya Menggunakan Kaki
Melisa Diana Putri adalah seorang siswi difabel di SDN Tukul II Kecamatan Sumber, Kabupaten Probolinggo, Jawa Timur. Melisa duduk di kelas 8. Ia bercita-cita menjadi guru. Semangatnya sangat tinggi meski ia belajar dan beraktivitas menggunakan kaki.
Melisa mengikuti pelajaran di sekolah bersama teman-temannya seperti biasa. Namun saat menulis di buku tulis, dia menggunakan jari kaki. Oleh sekolah, meja khusus dia menulis dibuat lebih rendah dari tubuhnya. Saat menulis di papan tulis untuk mengerjakan tugas dari guru, ia juga menggunakan kaki. Kaki kirinya menopang tubuh agar seimbang, sementara kaki kanannya lincah menulis di papan tulis. Meski menggunakan kaki sejak lahir, tulisan Melisa rapi.
Meskipun memiliki keterbatasan fisik, Melisa sangat tekun dalam belajar. Ia sangat bersemangat meraih prestasi dan nilai baik. Menurut pengakuan gurunya, Melisa memang sangat jago matematika. Selain itu, Melisa juga hobi membaca. Buku apa pun dia baca. Melisa mengaku, ia membaca buku untuk memperluas wawasan.
Menurut Tri Adi Nurfeni, guru Bahasa Indonesia, Melisa meraih cukup banyak prestasi. Melisa pernah juara lomba baca, tulis dan hitung tingkat kecamatan, dan ditunjuk menjadi duta sekolah karena pengetahuannya yang bagus. Berkat pencapaian Melisa, Wakil Bupati Timbul Prihanjoko mengunjungi Melisa di sekolah. Joko, panggilan akrab Wakil Bupati Probolinggi, terharu melihat semangat Melisa untuk meraih cita-cita. Joko dan sejumlah pejabat Pemkab Probolinggo memberi sejumlah bantuan untuk kelanjutan belajar Melisa.
Melisa menjadi bukti bahwa keterbatasan fisik tidak menghalangi seseorang dalam meraih prestasi. Berkat ketekunan dalam belajar, Melisa dapat menghilangkan keterbatasan-keterbatasan itu tadi.
(Sumber: Kompas.com, dengan penyesuaian)
Paragraf yang berisi bagian resolusi adalah ....



