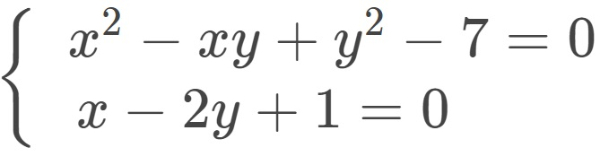Bank Soal Matematika SMA Sistem Persamaan Dua Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
The correct word to fill in the sentence number (III) is ....
Bahasa Inggris
Level 12
Bahasa Inggris
News Item
News Item
Berikut ini pernyataan yang tepat mengenai fase blastulasi adalah ....
Biologi
Level 12
Biologi
Pertumbuhan dan Perkembangan Makhluk Hidup
Pertumbuhan dan Perkembangan pada Hewan dan Manusia
Diketahui kubus memiliki panjang rusuk 20 cm. Titik dan masing-masing adalah titik tengah dan , sedangkan titik adalah titik potong diagonal bidang . Cosinus sudut antara dan alas adalah ....
Matematika
Level 12
Geometri
Dimensi Tiga (Geometri Ruang)
Sudut pada Bangun Ruang
Complete the dialogue based on the situation.

Your sister, Miranda, is coming home for holiday. She is going back by train alone. She needs someone to pick her up.
You: _____.
Miranda: Thanks a lot!
Bahasa Inggris
Level 12
Bahasa Inggris
Services
Asking for and Giving Services
Salah satu tokoh penting di kabinet Djuanda, gambar tokohnya diabadikan oleh pemerintah Indonesia dalam uang kertas pecahan ....
Sejarah Indonesia
Level 12
Kehidupan Politik dan Ekonomi Indonesia Masa Awal Kemerdekaan, Demokrasi Terpimpin, dan Demokrasi Liberal
Perkembangan Politik dan Ekonomi Indonesia (1945-1965)
Pada suhu 250 °C, tekanan uap air murni adalah 32 mmHg. Tekanan uap larutan 3 mol etanol dalam 25 mol air pada suhu 250 °C adalah ….
Kimia
Level 12
Sifat Koligatif Larutan
Penurunan Tekanan Uap
Perhatikan hasil pengukuran arus pada amperemeter di bawah ini!

Berdasarkan rangkaian listrik di atas, beda potensial pada ujung-ujung hambatan adalah ....
Fisika
Level 12
Fisika
Rangkaian Arus Searah
Rangkaian Arus Searah
Untuk mengatasi gangguan dengan gejala tubuh seperti gambar di bawah ini, hal-hal berikut yang bisa dilakukan, kecuali ....

Biologi
Level 12
Biologi
Enzim dan Metabolisme Sel
Katabolisme Lemak dan Protein
Hari kemenangan Pertempuran Ambarawa yaitu 15 Desember 1945 diperingati dan dijadikan sebagai hari bersejarah bagi TNI, yaitu ....
Sejarah Indonesia
Level 12
Upaya Bangsa Indonesia Menghadapi Ancaman Disintegrasi Bangsa
Upaya Bangsa Indonesia Mengatasi Ancaman Disintegrasi Bangsa
Nilai dari adalah ....
Matematika
Level 12
Trigonometri
Limit Fungsi Trigonometri
Nilai Limit Fungsi Trigonometri
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
The correct word to fill in the sentence number (III) is ....
Berikut ini pernyataan yang tepat mengenai fase blastulasi adalah ....
Diketahui kubus memiliki panjang rusuk 20 cm. Titik dan masing-masing adalah titik tengah dan , sedangkan titik adalah titik potong diagonal bidang . Cosinus sudut antara dan alas adalah ....
Complete the dialogue based on the situation.

Your sister, Miranda, is coming home for holiday. She is going back by train alone. She needs someone to pick her up.
You: _____.
Miranda: Thanks a lot!
Salah satu tokoh penting di kabinet Djuanda, gambar tokohnya diabadikan oleh pemerintah Indonesia dalam uang kertas pecahan ....
Pada suhu 250 °C, tekanan uap air murni adalah 32 mmHg. Tekanan uap larutan 3 mol etanol dalam 25 mol air pada suhu 250 °C adalah ….
Perhatikan hasil pengukuran arus pada amperemeter di bawah ini!
Berdasarkan rangkaian listrik di atas, beda potensial pada ujung-ujung hambatan adalah ....
Untuk mengatasi gangguan dengan gejala tubuh seperti gambar di bawah ini, hal-hal berikut yang bisa dilakukan, kecuali ....

Hari kemenangan Pertempuran Ambarawa yaitu 15 Desember 1945 diperingati dan dijadikan sebagai hari bersejarah bagi TNI, yaitu ....
Nilai dari adalah ....