Bank Soal Matematika SMA Aplikasi Integral
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
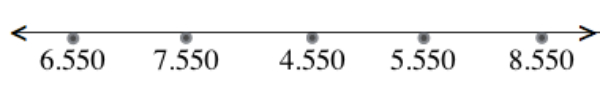
Garis bilangan yang tepat untuk memperbaiki garis bilangan di atas yang menunjukan urutan dari bilangan terkecil hingga bilangan terbesar adalah ....
Matematika
Level 3
Bilangan
Bilangan Cacah dan Pecahan Sederhana
Garis Bilangan (Bilangan Cacah dan Pecahan Sederhana)
Perhatikan gambar di bawah ini!

(Sumber: www.startfmmadina.com)
Kegunaan benda gas di atas adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi tentang Konsep
Menggali Informasi Konsep Perubahan Wujud Benda
Berikut ini adalah hasil laut yang terjual di sebuah perkampungan nelayan selama satu minggu.
- Kerang 45 kg
- Ikan tuna 60 kg
- Ikan salmon 25 kg
- Udang 40 kg
- Cumi 30 kg
Manakah dari tabel di bawah ini yang sesuai dengan data tersebut?
Matematika
Level 3
Statistika
Data
Mengumpulkan dan Menyajikan Data
Perhatikan denah berikut!
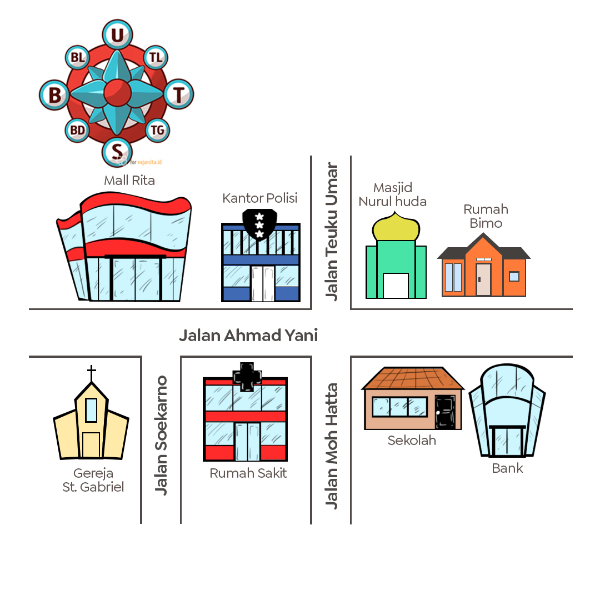
Bangunan yang berada di sebelah barat laut sekolah adalah ....
Bahasa Indonesia
Level 3
Menulis
Informasi Delapan Mata Angin
Membaca Denah
Nilai dari
 adalah ....
adalah ....
Matematika
Level 3
Bilangan
Pecahan Sederhana
Penjumlahan Pecahan Penyebut Sama
Perhatikan gambar berikut!

(Sumber: freepik.com)
Alat di atas digunakan untuk mengukur ....
Matematika
Level 3
Geometri
Pengukuran Waktu, Panjang, Berat
Alat Ukur Berat
Faiz mempunyai aquarium.
Air dalam aquarium habis dipindah ke dalam ember, seperti gambar berikut.

(Sumber Gambar: flaticon.com)
Arti dari gambaran di atas adalah ...
Matematika
Level 3
Geometri
Volume Bangun Ruang
Volume Bangun Ruang
Panjang persegi panjang 8 cm. Luas persegi panjang tersebut 40 cm2. Keliling persegi panjang ... cm.
Matematika
Level 3
Geometri
Bangun Datar
Keliling dan Luas Bangun Datar
30
Merupakan hasil kali dari bilangan ….
Matematika
Level 3
Bilangan
Operasi Hitung Bilangan Cacah
Operasi Hitung Bilangan Cacah
Cermati teks wawancara berikut ini!
Ola: Berapa banyak jumlah desa di Kelurahan Mekar Gemilang ini, Pak?
Pak Lurah: Ada 3 desa di Kelurahan Mekar Gemilang.
Ola: Apa nama ketiga desa tersebut, Pak?
Pak Lurah: Nama ketiga desa tersebut adalah Desa Mekar Abadi, Desa Mekar Sentosa, dan Desa Mekar Jaya.
Ola: Berapa jumlah kepala keluarga yang ada di masing-masing desa tersebut?
Pak Lurah: Desa Mekar Abadi terdiri atas 80 kepala keluarga. Desa Mekar Sentosa terdiri atas 90 kepala keluarga. Desa Mekar Jaya terdiri atas 100 kepala keluarga. Jadi, jumlah kepala keluarga di Kelurahan Mekar Gemilang ada 270 kepala keluarga.
Berdasarkan teks wawancara di atas, laporan hasil wawancara dalam bentuk tabel yang tepat adalah ...
Bahasa Indonesia
Level 3
Menulis
Wawancara
Menyajikan Laporan Hasil Wawancara
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Garis bilangan yang tepat untuk memperbaiki garis bilangan di atas yang menunjukan urutan dari bilangan terkecil hingga bilangan terbesar adalah ....
Perhatikan gambar di bawah ini!

(Sumber: www.startfmmadina.com)
Kegunaan benda gas di atas adalah ....
Berikut ini adalah hasil laut yang terjual di sebuah perkampungan nelayan selama satu minggu.
- Kerang 45 kg
- Ikan tuna 60 kg
- Ikan salmon 25 kg
- Udang 40 kg
- Cumi 30 kg
Manakah dari tabel di bawah ini yang sesuai dengan data tersebut?
Perhatikan denah berikut!
Bangunan yang berada di sebelah barat laut sekolah adalah ....
Nilai dari
adalah ....
Perhatikan gambar berikut!
(Sumber: freepik.com)
Alat di atas digunakan untuk mengukur ....
Faiz mempunyai aquarium.
Air dalam aquarium habis dipindah ke dalam ember, seperti gambar berikut.
(Sumber Gambar: flaticon.com)
Arti dari gambaran di atas adalah ...
Panjang persegi panjang 8 cm. Luas persegi panjang tersebut 40 cm2. Keliling persegi panjang ... cm.
30
Merupakan hasil kali dari bilangan ….
Cermati teks wawancara berikut ini!
Ola: Berapa banyak jumlah desa di Kelurahan Mekar Gemilang ini, Pak?
Pak Lurah: Ada 3 desa di Kelurahan Mekar Gemilang.
Ola: Apa nama ketiga desa tersebut, Pak?
Pak Lurah: Nama ketiga desa tersebut adalah Desa Mekar Abadi, Desa Mekar Sentosa, dan Desa Mekar Jaya.
Ola: Berapa jumlah kepala keluarga yang ada di masing-masing desa tersebut?
Pak Lurah: Desa Mekar Abadi terdiri atas 80 kepala keluarga. Desa Mekar Sentosa terdiri atas 90 kepala keluarga. Desa Mekar Jaya terdiri atas 100 kepala keluarga. Jadi, jumlah kepala keluarga di Kelurahan Mekar Gemilang ada 270 kepala keluarga.
Berdasarkan teks wawancara di atas, laporan hasil wawancara dalam bentuk tabel yang tepat adalah ...



