Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Dari 10 pekarangan rumah yang ada di RT 01, ada 5 yang ditanami pohon cabai. Berapa bagiankah pekarangan di RT 01 yang terdapat pohon cabainya?
Matematika
Level 4
Bilangan
Pecahan
Pecahan Senilai
Rumus untuk mencari luas segitiga adalah ...
Matematika
Level 4
Geometri
Bangun Datar
Keliling dan Luas Segitiga
Di bawah ini adalah macam-macam karya sastra, kecuali ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Vocabulary: Jobs
Perhatikan tabel di bawah ini!

Nilai p yang tepat adalah …
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Faktor Bilangan
Poligon yang mempunyai 7 sisi dinamakan?
Matematika
Level 4
Geometri
Bangun Datar
Segi Banyak
Seorang pedagang mempunyai 40 ekor ayam dan 50 ekor utik akan dimasukkan ke dalam kandang sama banyak. Banyak kandang terbanyak yang harus disiapkan adalah ... kandang.
Matematika
Level 4
Bilangan
FPB dan KPK
FPB
Reza sedang mengerjakan ujian Matematika sebanyak 40 soal.
3 soal tidak dikerjakan Reza karena susah.
Banyak soal yang dijawab benar oleh Reza 11 kali banyak soal yang tidak dia jawab.
Soal yang dijawab salah oleh Reza adalah … soal.
Bahasa Indonesia
Level 3
Membaca
Teks Fiksi-Tokoh Cerita
Dongeng
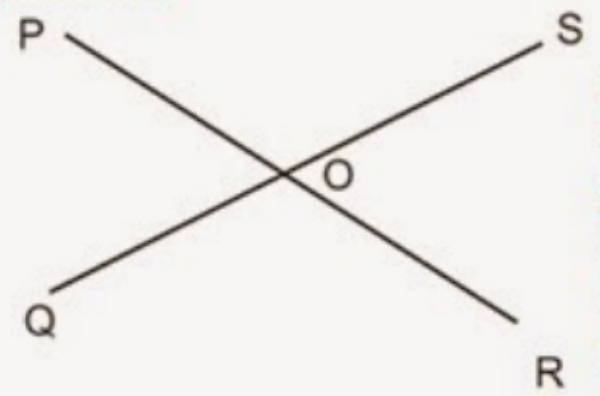
Bila POQ adalah 50, maka besar QOR adalah ....
Matematika
Level 4
Geometri
Garis dan Sudut
Sudut
Perhatikan tabel berikut.

Kelas manakah yang mempunyai jumlah murid paling sedikit?
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Dari 10 pekarangan rumah yang ada di RT 01, ada 5 yang ditanami pohon cabai. Berapa bagiankah pekarangan di RT 01 yang terdapat pohon cabainya?
Rumus untuk mencari luas segitiga adalah ...
Di bawah ini adalah macam-macam karya sastra, kecuali ....
Fill the blanks with 'a' or 'an'.
1. I want to be ... surgeon.
2. She is ... architect.
The correct answers for number 1 and 2 are ....
Perhatikan tabel di bawah ini!
Nilai p yang tepat adalah …
Poligon yang mempunyai 7 sisi dinamakan?
Seorang pedagang mempunyai 40 ekor ayam dan 50 ekor utik akan dimasukkan ke dalam kandang sama banyak. Banyak kandang terbanyak yang harus disiapkan adalah ... kandang.
Reza sedang mengerjakan ujian Matematika sebanyak 40 soal.
3 soal tidak dikerjakan Reza karena susah.
Banyak soal yang dijawab benar oleh Reza 11 kali banyak soal yang tidak dia jawab.
Soal yang dijawab salah oleh Reza adalah … soal.
Bila POQ adalah 50, maka besar QOR adalah ....
Perhatikan tabel berikut.
Kelas manakah yang mempunyai jumlah murid paling sedikit?



