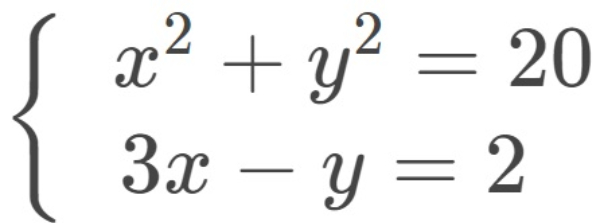Bank Soal Matematika SMA Sistem Persamaan Dua Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Jenis sitoskeleton yang menyusun rambut manusia adalah ....
Biologi
Level 11
Biologi
Sel
Struktur dan Fungsi Sel
Choose the right answer.

Sherly: What do you think of my appearance? Do I look okay with this dress?
Rachel: You look fabulous! But it will be more elegant if you wear these necklaces.
Sherly: That’s right!
The underlined sentence is the expression of ...
Bahasa Inggris
Level 11
Good Advice
Giving Advice or Suggestions
Jika setiap titik pada parabola ditranslasikan menurut 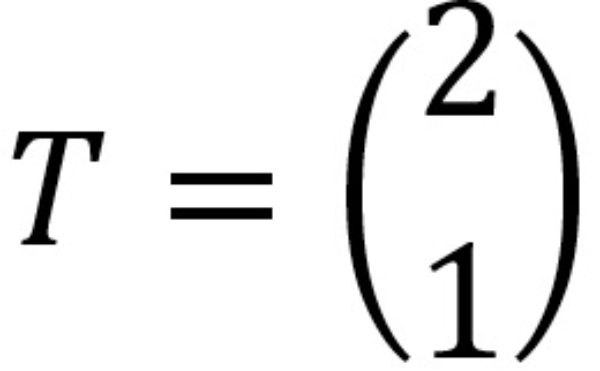 maka parabola yang dihasilkan adalah ....
maka parabola yang dihasilkan adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
Diketahui menyatakan bahwa habis dibagi 6. Diandaikan benar untuk , artinya ....
Matematika
Level 11
Logika
Induksi Matematika
Induksi Matematika pada Keterbagian
Salah satu kegunaan senyawa hidrokarbon dalam kehidupan sehari-hari adalah proses pengelasan pada suatu logam. Pada proses pengelasan, digunakan suatu gas dari golongan alkuna yang merupakan hasil reaksi dari kalsium karbida dengan air. Gas yang dimaksud adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Pernyataan yang benar tentang momen inersia adalah ....
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Dinamika Benda Tegar
Protein transpor berperan dalam transportasi zat seperti asam amino dan glukosa. Tidak adanya protein transpor ini bisa menyebabkan terjadinya suatu penyakit yang ditandai dengan terdapatnya sistein dalam jumlah besar pada air seni. Keberadaan sistein ini bisa menyebabkan terjadinya batu ginjal apabila asam amino itu terkristalisasi. Penyakit yang dimaksud dari pernyataan tersebut adalah ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Berikut ini yang merupakan isomer kerangka dari senyawa 2-heksena adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Jika , maka nilai dari adalah ........
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Persamaan Trigonometri
Perhatikan tabel emisi karbon dioksida dalam setahun dari negara-negara berikut!

Negara mana yang memiliki emisi per kapita terkecil?
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Jenis sitoskeleton yang menyusun rambut manusia adalah ....
Choose the right answer.

Sherly: What do you think of my appearance? Do I look okay with this dress?
Rachel: You look fabulous! But it will be more elegant if you wear these necklaces.
Sherly: That’s right!
The underlined sentence is the expression of ...
Jika setiap titik pada parabola ditranslasikan menurut 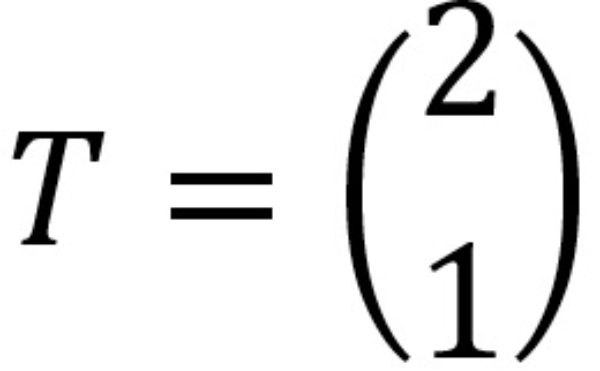
Diketahui menyatakan bahwa habis dibagi 6. Diandaikan benar untuk , artinya ....
Salah satu kegunaan senyawa hidrokarbon dalam kehidupan sehari-hari adalah proses pengelasan pada suatu logam. Pada proses pengelasan, digunakan suatu gas dari golongan alkuna yang merupakan hasil reaksi dari kalsium karbida dengan air. Gas yang dimaksud adalah ....
Pernyataan yang benar tentang momen inersia adalah ....
Protein transpor berperan dalam transportasi zat seperti asam amino dan glukosa. Tidak adanya protein transpor ini bisa menyebabkan terjadinya suatu penyakit yang ditandai dengan terdapatnya sistein dalam jumlah besar pada air seni. Keberadaan sistein ini bisa menyebabkan terjadinya batu ginjal apabila asam amino itu terkristalisasi. Penyakit yang dimaksud dari pernyataan tersebut adalah ....
Berikut ini yang merupakan isomer kerangka dari senyawa 2-heksena adalah ....
Jika , maka nilai dari adalah ........
Perhatikan tabel emisi karbon dioksida dalam setahun dari negara-negara berikut!
Negara mana yang memiliki emisi per kapita terkecil?