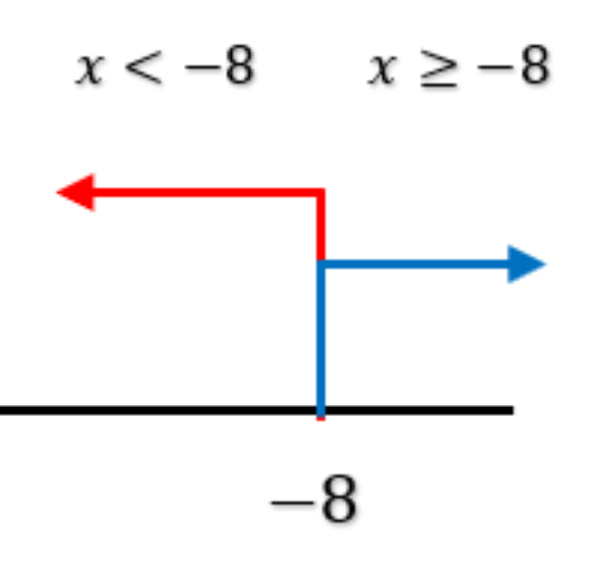
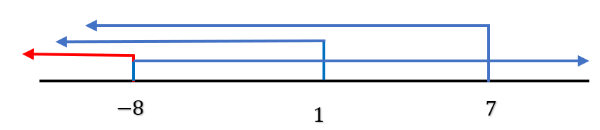
Bank Soal Matematika SMA Pertidaksamaan Linear Satu Variabel dengan Nilai Mutlak

Soal

Pilgan

Himpunan penyelesaian dari pertidaksamaan nilai mutlak 4x+∣x+8∣≤134x+\left|x+8\right|\le13 adalah ....

A

HP ={x∣x>7, x∈R}=\left\{x\mid x>7,\ x\in R\right\}

B

HP ={x∣x≥1, x∈R}=\left\{x\mid x\ge1,\ x\in R\right\}

C

HP ={x∣x≥−8, x∈R}=\left\{x\mid x\ge-8,\ x\in R\right\}

D

HP ={x∣x<−8, x∈R}=\left\{x\mid x<-8,\ x\in R\right\}

E

HP ={x∣x<1 x∈R}=\left\{x\mid x<1\ x\in R\right\}

Pembahasan:

Persoalan tersebut dapat diselesaikan berdasarkan definisi nilai mutlak, di mana untuk setiap bilangan real xx, nilai mutlak ∣x∣\left|x\right| ditentukan oleh:

∣x∣=+x\left|x\right|=+x, untuk x>0x>0

∣x∣=0\left|x\right|=0, untuk x=0x=0

∣x∣=−x\left|x\right|=-x, untuk x<0x<0


1) Mencari batas dari ∣x+8∣\left|x+8\right|

x+8=0x+8=0

x=−8x=-8

Diperoleh interval dengan gambar:

2) Diperoleh persamaan berikut.

∣x+8∣=x+8\left|x+8\right|=x+8, jika x≥−8x\ge-8

∣x+8∣=−(x+8)\left|x+8\right|=-\left(x+8\right), jika x<−8x<-8


untuk x≥−8x\ge-8, bentuk pertidaksamaannya menjadi:

4x+∣x+8∣≤134x+\left|x+8\right|\le13

4x+x+8≤134x+x+8\le13

5x≤13−85x\le13-8

5x≤55x\le5

x≤55x\le\frac{5}{5}

x≤1x\le1


untuk x<−8x<-8, bentuk pertidaksamaannya menjadi:

4x+∣x+8∣≤134x+\left|x+8\right|\le13

4x+(−(x+8))≤134x+\left(-\left(x+8\right)\right)\le13

4x−x−8≤134x-x-8\le13

3x≤13+83x\le13+8

3x≤213x\le21

x≤213x\le\frac{21}{3}

x≤7x\le7


Selanjutnya dapat digambarkan penyelesaiannya pada garis bilangan berikut.


Jadi, HP ={x∣x<−8, x∈R}=\left\{x\mid x<-8,\ x\in R\right\}

Video
16 Maret 2020
Sudut | Matematika | Kelas IV
✔ Ingin tanya tutor?
✔ Cek sampel tanya jawab
Rangkuman
08 April 2020
Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya
Lihat Semua Rangkuman dan Materi

Siswa

Ingin latihan soal, nonton, atau unduh materi belajar lebih banyak?

Buat Akun Gratis

Guru

Ingin akses bank soal, nonton, atau unduh materi belajar lebih banyak?

Buat Akun Gratis

Soal Populer Hari Ini

Hasil dari 15×(14+15)\frac{1}{5}\times\left(\frac{1}{4}+\frac{1}{5}\right) adalah ...

Matematika Level 6 Bilangan Operasi Hitung Bilangan Bulat dan Pecahan Operasi Hitung Campuran Kelas VI Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Complete the sentence below.

Premium Vector | Travel by car on holiday

Source: pinterest.com

Last holiday, my friends and I (1) ______. We went there by (2) ______. There, we (3) ______. It was a fun holiday!

The best word to complete point (2) is ....

Bahasa Inggris Level 6 Bahasa Inggris Past Holidays Recount Text Kelas VI Kurikulum 2013 K13
Lihat selengkapnya

Kalimat tanya yang sesuai untuk menanyakan informasi pada kalimat ketiga paragraf pertama adalah ….

Bahasa Indonesia Level 6 Membaca Buku Sejarah Menggali Informasi (5W+1H)
Lihat selengkapnya

Jari-jari alas sebuah tabung 10 cm dan tingginya 25 cm. luas permukaan tabung adalah … cm2. (π\pi = 227\frac{22}{7} ) (UASBN 2007/2008)

Matematika Level 6 Geometri Bangun Ruang Volume dan Luas Permukaan Bangun Ruang Tabung Kelas VI Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Di dalam ruangan terdapat 15 tumpuk piring. Setiap tumpuk berisi 25 buah. Piring-piring tersebut akan dimasukkan ke dalam kardus. Setiap kardus berisi 12 buah. Banyak piring yang tidak masuk kardus adalah ...

Matematika Level 6 Bilangan Operasi Hitung Bilangan Bulat dan Pecahan Operasi Hitung Bilangan Bulat Kelas VI Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Adik mempunyai sebuah celengan berbentuk prisma dengan alas dan tutupnya berbentuk lingkaran. Jika jari-jari lingkaran tersebut adalah 2 cm dan tinggi celengan adalah 6 cm, maka volume celengan adik adalah ... cm3 ( Gunakan π\pi = 3,14 )

Matematika Level 6 Geometri Bangun Ruang Volume dan Luas Permukaan Bangun Ruang Tabung Kelas VI Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Perhatikan ciri-ciri pubertas di bawah ini!

  1. Tumbuh rambut kumis
  2. Dada membidang
  3. Panggul membesar
  4. Suara menjadi berat
  5. Mengalami haid atau menstruasi

Ciri-ciri pubertas pada anak perempuan ditunjuk oleh nomor ....

IPA Level 6 Biologi Perkembangbiakan Makhluk Hidup Pubertas pada Manusia
Lihat selengkapnya

Data tinggi badan siswa kelas VI SD Ceria (dalam cm) sebagai berikut :

137, 130, 130, 137, 135, 135, 130, 130, 130, 137, 134, 137, 134, 135, 137, 137, 135, 137, 135, 130, 135, 134, 134, 130, 134, 135, 130, 134, 135, 134, 134, dan 135.

Modus data tersebut adalah ...

Matematika Level 6 Statistika Data Tunggal Modus Kelas VI Kurikulum 2013 K13 Matematika
Lihat selengkapnya

Bacalah laporan berikut!

Pada hari Senin tanggal 10 Juni 2019, ibu guru memberi tugas kepada siswa kelas VI SD Bensoleh untuk meneliti bunga-bunga yang ditanam di taman sekolah. Banyak bunga yang ditanam atau tumbuh sendiri di taman sekolah. Bunga-bunga hias, seperti bunga mawar, bunga krisantemum, kamboja, dan kaktus ditanam rapi di taman sekolah. Selain bunga hias, bunga pacar air dan bunga kertas yang tumbuh liar juga dirawat dengan baik. [...]

Simpulan yang tepat untuk melengkapi teks laporan hasil pengamatan di atas agar menjadi laporan yang padu adalah ...

Bahasa Indonesia Level 6 Menulis Teks Laporan Hasil Pengamatan Menulis Teks Laporan
Lihat selengkapnya

Perhatikan contoh perkembangbiakan secara vegatatif di bawah ini!

  1. Umbi lapis
  2. Umbi batang
  3. Cangkok
  4. Tunas adventif
  5. Merunduk

Perkembangbiakan secara vegetatif alami ditunjuk oleh nomor ....

IPA Level 6 Biologi Perkembangbiakan Makhluk Hidup Perkembangbiakan Tumbuhan Kelas VI Kurikulum 2013 K13 IPA
Lihat selengkapnya
✔ Ingin soal latihan HOTS?
✔ Cek sampel soal HOTS?

Cek Contoh Kuis Online

Kejar Kuis

Cek Contoh Bank Soal

Kejar Soal