Bank Soal Matematika SMA Operasi Invers Komposisi Fungsi
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini

(Sumber Gambar: pinterest.com)
Banyaknya anak di kelas adalah ... orang.
Matematika
Level 1
Bilangan
Mengenal Bilangan Cacah (0-100)
Menghitung Jumlah Benda/Orang
Hal yang harus diperhatikan saat membaca adalah sebagai berikut, kecuali ....
Bahasa Indonesia
Level 1
Membaca
Membaca Permulaan
Persiapan Membaca
Ada 7 lingkaran pada kotak.
Kotak akan penuh bila berisi 10 lingkaran.
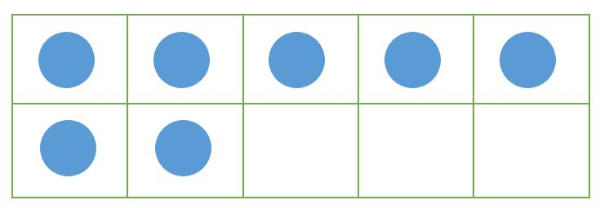
Berapa banyak lingkaran lagi yang kamu butuhkan untuk membuat kotak penuh?
Matematika
Level 1
Bilangan
Penjumlahan dan Pengurangan Bilangan Cacah
Penjumlahan dan Pengurangan Bilangan Cacah
Lanjutkan urutan angka di bawah ini.
7, 10, 13, ....
Matematika
Level 1
Bilangan
Pola Bilangan
Memprediksi dan Membuat Pola Bilangan
Kegiatan dengan waktu paling lama adalah ...
Matematika
Level 1
Bilangan
Mengenal Satuan Waktu, Panjang, dan Berat
Mengenal Satuan Waktu Tidak Baku

Ana dan James sedang bermain boneka salju.
Boneka salju mereka memiliki mata, hidung, dan juga mulut.
Hidung boneka salju memiliki bentuk ....
Matematika
Level 1
Geometri
Mengenal Bangun Ruang
Menebak Bentuk Benda

(Sumber Gambar: freepik.com)
Pola gambar bola basket selanjutnya adalah ....
Matematika
Level 1
Geometri
Mengenal Bangun Datar
Pola Pengubinan
Bu Guru menyuruh Ana, Desi, Ratna, dan Sari untuk memilih sebuah bilangan.
Bilangan yang dipilih masing-masing, digambarkan sebagai berikut.

(Sumber Gambar: freepik.com)
Nama bilangan yang dipilih Ana dan Sari secara berturut- turut adalah ....
Matematika
Level 1
Bilangan
Mengenal Bilangan Cacah (0-100)
Lambang Bilangan
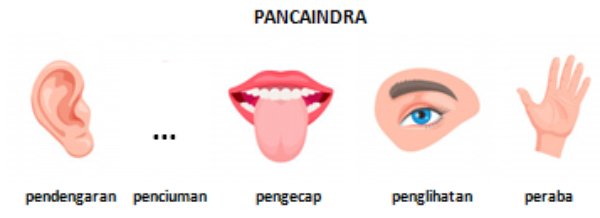
Gambar yang tepat untuk mengisi indra penciuman adalah ....
Bahasa Indonesia
Level 1
Menulis
Anggota Tubuh
Fungsi Anggota Tubuh (Pancaindra)
Kegiatan yang membutuhkan waktu lebih lama, kecuali ....
Matematika
Level 1
Bilangan
Mengenal Satuan Waktu, Panjang, dan Berat
Membandingkan Lamanya Waktu
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
(Sumber Gambar: pinterest.com)
Banyaknya anak di kelas adalah ... orang.
Hal yang harus diperhatikan saat membaca adalah sebagai berikut, kecuali ....
Ada 7 lingkaran pada kotak.
Kotak akan penuh bila berisi 10 lingkaran.
Berapa banyak lingkaran lagi yang kamu butuhkan untuk membuat kotak penuh?
Lanjutkan urutan angka di bawah ini.
7, 10, 13, ....
Kegiatan dengan waktu paling lama adalah ...
Ana dan James sedang bermain boneka salju.
Boneka salju mereka memiliki mata, hidung, dan juga mulut.
Hidung boneka salju memiliki bentuk ....
(Sumber Gambar: freepik.com)
Pola gambar bola basket selanjutnya adalah ....
Bu Guru menyuruh Ana, Desi, Ratna, dan Sari untuk memilih sebuah bilangan.
Bilangan yang dipilih masing-masing, digambarkan sebagai berikut.
(Sumber Gambar: freepik.com)
Nama bilangan yang dipilih Ana dan Sari secara berturut- turut adalah ....
Gambar yang tepat untuk mengisi indra penciuman adalah ....
Kegiatan yang membutuhkan waktu lebih lama, kecuali ....