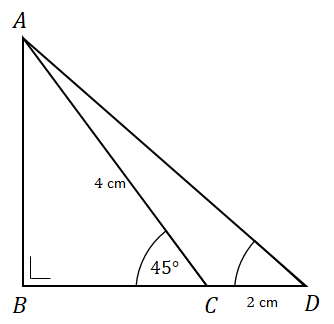
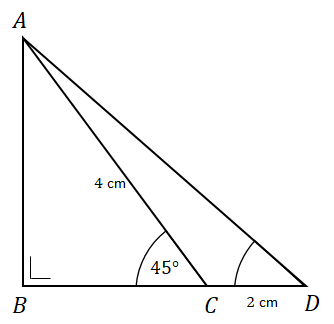
Bank Soal Matematika SMA Aplikasi Rasio Trigonometri
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Di bawah ini yang merupakan kalimat terbuka adalah …
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Kalimat Benar, Salah, dan Terbuka
(i) 24816= 321616:232
(ii) 8127:93= 24327:279:81
(iii) ((-98)7)6:(-34)5(-12)= 3652
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
Perhatikan himpunan di bawah ini.
A = {t, e, h}
B = {t, h, e}
C = {x|x adalah lima bilangan cacah pertama}
D = {1, 2, 3, 4, 5}
Himpunan di atas yang sama adalah … .
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Perhatikan gambar berikut!
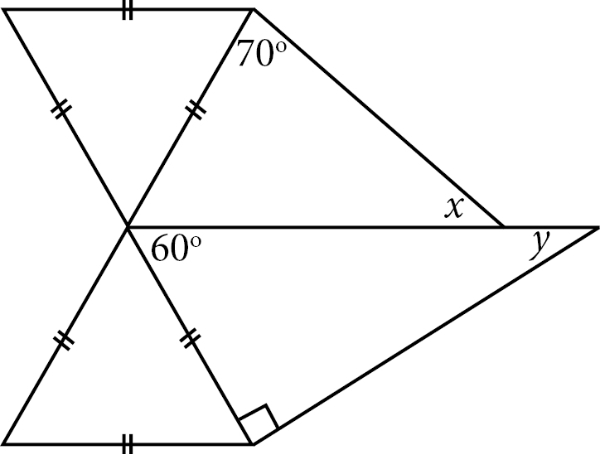
Nilai dari adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Hubungan Antar Sudut
Pernyataan berikut yang termasuk ciri-ciri teks deskripsi adalah ....
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Ciri dan Tujuan Teks Deskripsi
Hasil dari
Matematika
Level 7
Aljabar
Bentuk Aljabar
Operasi Hitung Bentuk Aljabar
Cermati contoh surat berikut ini.

Surat tersebut ditujukan kepada ....
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Unsur-unsur dan Kebahasaan Surat
“Sedikit kelemahan buku ini adalah banyaknya penggunaan istilah-istilah lokal sehingga mengganggu pemahaman pembaca yang belum memahami daerah tersebut.”
Kalimat tersebut merupakan contoh komentar yang menilai ....
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Komentar terhadap Buku Fiksi dan Nonfiksi
Kegiatan di bawah ini merupakan proses yang dilakukan dalam statistika, kecuali ....
Matematika
Level 7
Statistika
Penyajian dan Pengolahan Data
Penyajian dan Pengolahan Data
Read the text below and fill the blanks with correct answers according to the relationship to the writer.
This is my family. Every holiday, my aunt and uncle bring their son Andre to visit me. He is my ... (1). My brother and his wife also come to visit my parents. They have a son, named Angga, my cute ... (2). My mother and father would really love to meet their ..., Angga (3).
The best word to fill number (2) is ....
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Vocabulary: Family Tree
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Di bawah ini yang merupakan kalimat terbuka adalah …
(i) 24816= 321616:232
(ii) 8127:93= 24327:279:81
(iii) ((-98)7)6:(-34)5(-12)= 3652
Perhatikan himpunan di bawah ini.
A = {t, e, h}
B = {t, h, e}
C = {x|x adalah lima bilangan cacah pertama}
D = {1, 2, 3, 4, 5}
Himpunan di atas yang sama adalah … .
Perhatikan gambar berikut!
Nilai dari adalah ....
Pernyataan berikut yang termasuk ciri-ciri teks deskripsi adalah ....
Hasil dari
Cermati contoh surat berikut ini.
Surat tersebut ditujukan kepada ....
“Sedikit kelemahan buku ini adalah banyaknya penggunaan istilah-istilah lokal sehingga mengganggu pemahaman pembaca yang belum memahami daerah tersebut.”
Kalimat tersebut merupakan contoh komentar yang menilai ....
Kegiatan di bawah ini merupakan proses yang dilakukan dalam statistika, kecuali ....
Read the text below and fill the blanks with correct answers according to the relationship to the writer.
This is my family. Every holiday, my aunt and uncle bring their son Andre to visit me. He is my ... (1). My brother and his wife also come to visit my parents. They have a son, named Angga, my cute ... (2). My mother and father would really love to meet their ..., Angga (3).
The best word to fill number (2) is ....