Bank Soal Matematika SMA Teorima Sisa dan Teorema Faktor
Soal
Matematika Peminatan LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Sebuah dadu dilempar 46 kali. Frekuensi harapan muncul mata dadu bilangan prima adalah...
Matematika
Level 8
Statistika
Peluang
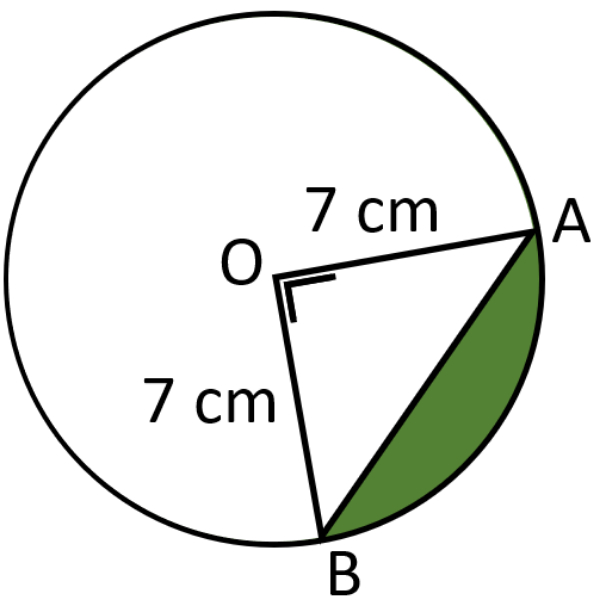
Luas daerah yang berwarna hijau adalah ... cm2 ( Gunakan = )
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
Kelas VIII
Kurikulum 2013
K13
Matematika
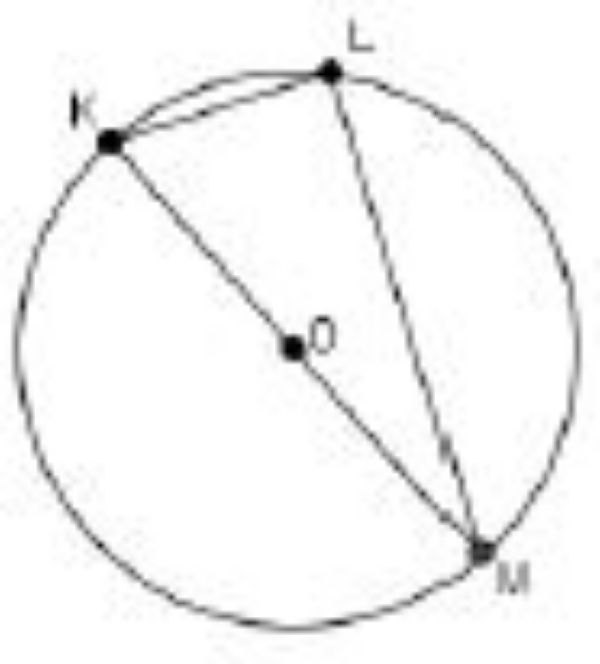
Jika sudut MKL = 54o , KLM = 90o, dan KM merupakan diameter lingkaran. Hitunglah besar sudut KML!
Matematika
Level 8
Geometri
Lingkaran
Sudut Pusat dan Sudut Keliling
Kelas VIII
Kurikulum 2013
K13
Matematika
Di antara pasangan titik koordinat berikut ini, yang terletak di kuadran I dan II adalah?
(i) (1, 2) dan (2, 4)
(ii) (2, -3) dan (3, -2)
(iii) (-4, 7) dan (-1, 4)
(iv) (-2, -5) dan (-2, -1)
Matematika
Level 8
Geometri
Koordinat Kartesius
Kuadran
Kelas VIII
Kurikulum 2013
K13
Matematika
Syarat informasi yang layak diangkat menjadi sebuah berita adalah memiliki sifat ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Simpulan Isi Berita
KD4.1
Kelas VIII
Kurikulum 2013
K13
Bahasa Indonesia
Read the following teacher’s talk.

Source: shutterstock.com
"Well done, everyone. You did your best in your English speech today. However, some of you still need to speak more confidently."
The comparison form of “more confidently” refers to ….
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Kelas VIII
Kurikulum 2013
K13
Segitiga siku-siku SRQ digambar pada bidang koordinat sebagai berikut :
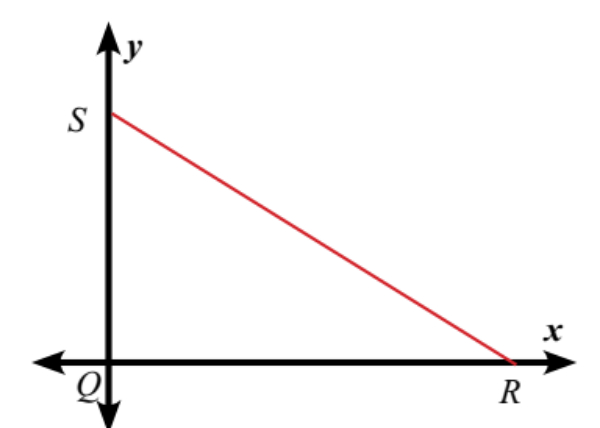
Jika panjang QR adalah 7 satuan dan panjang QS adalah 5 satuan, maka titik-titik koordinat Q, R, dan S secara berurutan adalah?
Matematika
Level 8
Geometri
Koordinat Kartesius
Posisi Titik terhadap Titik Tertentu
Kelas VIII
Kurikulum 2013
K13
Matematika
Unsur yang bersifat tersirat dan disampaikan penyair melalui kata, larik, dan bait dalam puisi adalah definisi dari salah satu unsur pembangun puisi yaitu ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
KD3.7
Kelas VIII
Kurikulum 2013
K13
Bahasa Indonesia
Agar iklan menarik, maka harus diperhatikan hal berikut, kecuali ....
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Pola penyajian dan Kebahasaan Iklan, Slogan, Poster
KD3.4
Kelas VIII
Kurikulum 2013
K13
Bahasa Indonesia
You were asked by your dance art teacher to collect data of students who can dance. The students, later, will be appointed to perform a traditional dance in an art festival next month. When you want to ask Adam, one of your friends, whether he can dance or not, you say ....
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Explaining Abilities
Kelas VIII
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Sebuah dadu dilempar 46 kali. Frekuensi harapan muncul mata dadu bilangan prima adalah...
Luas daerah yang berwarna hijau adalah ... cm2 ( Gunakan = )
Jika sudut MKL = 54o , KLM = 90o, dan KM merupakan diameter lingkaran. Hitunglah besar sudut KML!
Di antara pasangan titik koordinat berikut ini, yang terletak di kuadran I dan II adalah?
(i) (1, 2) dan (2, 4)
(ii) (2, -3) dan (3, -2)
(iii) (-4, 7) dan (-1, 4)
(iv) (-2, -5) dan (-2, -1)
Syarat informasi yang layak diangkat menjadi sebuah berita adalah memiliki sifat ....
Read the following teacher’s talk.

Source: shutterstock.com
"Well done, everyone. You did your best in your English speech today. However, some of you still need to speak more confidently."
The comparison form of “more confidently” refers to ….
Segitiga siku-siku SRQ digambar pada bidang koordinat sebagai berikut :
Jika panjang QR adalah 7 satuan dan panjang QS adalah 5 satuan, maka titik-titik koordinat Q, R, dan S secara berurutan adalah?
Unsur yang bersifat tersirat dan disampaikan penyair melalui kata, larik, dan bait dalam puisi adalah definisi dari salah satu unsur pembangun puisi yaitu ....
Agar iklan menarik, maka harus diperhatikan hal berikut, kecuali ....
You were asked by your dance art teacher to collect data of students who can dance. The students, later, will be appointed to perform a traditional dance in an art festival next month. When you want to ask Adam, one of your friends, whether he can dance or not, you say ....