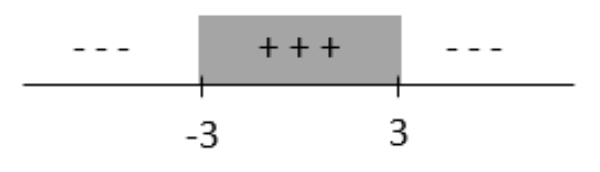
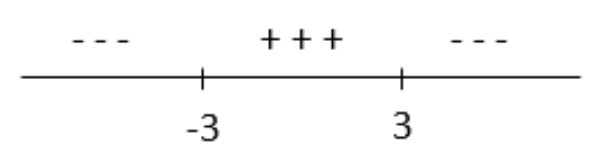Bank Soal Matematika SMA Pertidaksamaan Rasional
Soal
Matematika Wajib LOTS
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Perhatikan pernyataan-pernyataan di bawah ini!
1) Contohnya adalah tundra dan taiga
2) Contohnya adalah sawah dan danau
3) Penamaan berdasarkan jumlah populasi terbanyak.
4) Penamaan berdasarkan tumbuhan yang mendominasi.
5) Spesiesnya tergantung pada tingkat kecepatan reproduksi.
6) Spesiesnya tergantung pada iklim regionalnya.
Pernyataan-pernyataan yang benar mengenai bioma adalah ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Objek dan Permasalahan Biologi
To support her friend, Amy gives a complement to Kelly by saying ...
Bahasa Inggris
Level 10
Congratulating and Complimenting
Expressions of Congratulating and Complimenting
Sebuah tabung penampungan air mengalami kebocoran. Terdapat dua lubang di posisi ketinggian yang berbeda. Ternyata, dari masing-masing lubang menghasilkan bentuk aliran air yang berbeda. Melihat kejadian tersebut, salah seorang anak menjadi teringat materi fisika yang pernah dia pelajari di sekolah. Dia mulai tertarik untuk melakukan percobaan itu di rumah. Tapi, sebelum melakukan percobaan, dia pun mencari informasi di internet dan buku-buku terlebih dahulu sebagai dasar melakukan percobaannya. Di dalam metode ilmiah, proses ini merupakan tahap ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Hakikat dan Peran Fisika
Daerah pada ekosistem air laut yang memungkinkan terjadinya fotosintesis adalah ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Tipe Ekosistem
EDIT: jawaban seharusnya adalah HP
Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Pertidaksamaan Linear Satu Variabel dengan Nilai Mutlak
Penulisan huruf kapital yang salah terdapat pada kalimat …
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Menulis Teks Laporan Hasil Observasi
Ilmu yang mempelajari hubungan timbal balik antara makhluk hidup dan lingkungannya di dalam suatu ekosistem disebut dengan istilah ....
Biologi
Level 10
Biologi
Ekologi
Ekologi dan Komponen Ekosistem
Perhatikan gejala penyakit berikut!
- Demam
- Sakit kepala
- Pegal linu otot
- Sakit tenggorokan
- Hidung bersin
- Kehilangan nafsu makan
Penyakit dari gejala di atas disebabkan oleh virus ....
Biologi
Level 10
Biologi
Virus
Klasifikasi dan Peranan Virus dalam Kehidupan
Perhatikan alat-alat laboratorium berikut ini!
- Labu ukur
- Kaki tiga
- Gelas arloji
- Penjepit tabung
- Lampu spiritus
Pada saat kelas praktikum kimia, Intan ingin memanaskan larutan yang ada di dalam gelas kimia. Peralatan yang dibutuhkan untuk melakukan aktivitas tersebut adalah ....
Kimia
Level 10
Perkenalan Ilmu Kimia
Metode Ilmiah dan Laboratorium Kimia
Pertidaksamaan yang tepat untuk daerah penyelesaian di bawah ini adalah ....

Matematika
Level 10
Aljabar
Sistem Pertidaksamaan Dua Variabel
Pertidaksamaan Dua Variabel
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Perhatikan pernyataan-pernyataan di bawah ini!
1) Contohnya adalah tundra dan taiga
2) Contohnya adalah sawah dan danau
3) Penamaan berdasarkan jumlah populasi terbanyak.
4) Penamaan berdasarkan tumbuhan yang mendominasi.
5) Spesiesnya tergantung pada tingkat kecepatan reproduksi.
6) Spesiesnya tergantung pada iklim regionalnya.
Pernyataan-pernyataan yang benar mengenai bioma adalah ....
To support her friend, Amy gives a complement to Kelly by saying ...
Sebuah tabung penampungan air mengalami kebocoran. Terdapat dua lubang di posisi ketinggian yang berbeda. Ternyata, dari masing-masing lubang menghasilkan bentuk aliran air yang berbeda. Melihat kejadian tersebut, salah seorang anak menjadi teringat materi fisika yang pernah dia pelajari di sekolah. Dia mulai tertarik untuk melakukan percobaan itu di rumah. Tapi, sebelum melakukan percobaan, dia pun mencari informasi di internet dan buku-buku terlebih dahulu sebagai dasar melakukan percobaannya. Di dalam metode ilmiah, proses ini merupakan tahap ....
Daerah pada ekosistem air laut yang memungkinkan terjadinya fotosintesis adalah ....
EDIT: jawaban seharusnya adalah HP
Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah ....
Penulisan huruf kapital yang salah terdapat pada kalimat …
Ilmu yang mempelajari hubungan timbal balik antara makhluk hidup dan lingkungannya di dalam suatu ekosistem disebut dengan istilah ....
Perhatikan gejala penyakit berikut!
- Demam
- Sakit kepala
- Pegal linu otot
- Sakit tenggorokan
- Hidung bersin
- Kehilangan nafsu makan
Penyakit dari gejala di atas disebabkan oleh virus ....
Perhatikan alat-alat laboratorium berikut ini!
- Labu ukur
- Kaki tiga
- Gelas arloji
- Penjepit tabung
- Lampu spiritus
Pada saat kelas praktikum kimia, Intan ingin memanaskan larutan yang ada di dalam gelas kimia. Peralatan yang dibutuhkan untuk melakukan aktivitas tersebut adalah ....
Pertidaksamaan yang tepat untuk daerah penyelesaian di bawah ini adalah ....