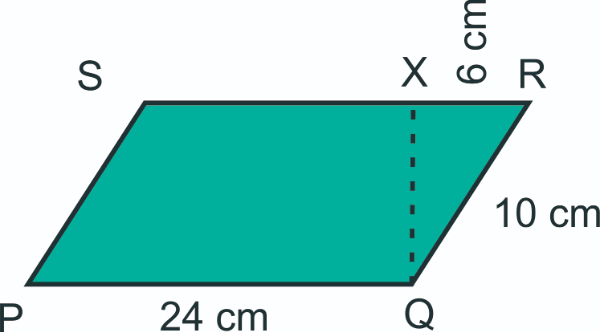
Bank Soal Matematika SMP Segitiga dan Teorema Pythagoras
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Dalam percobaan pengetosan dua koin, banyaknya ruang sampel yang terjadi yaitu ....
Matematika
Level 8
Statistika
Peluang
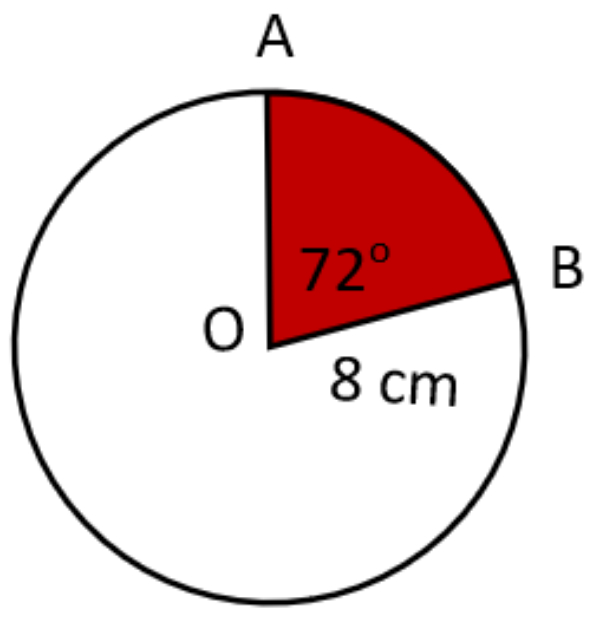
Luas daerah yang berwarna merah adalah ... cm2. ( Gunakan )
Matematika
Level 8
Geometri
Lingkaran
Luas dan Keliling Lingkaran
Perhatikan gambar berikut!
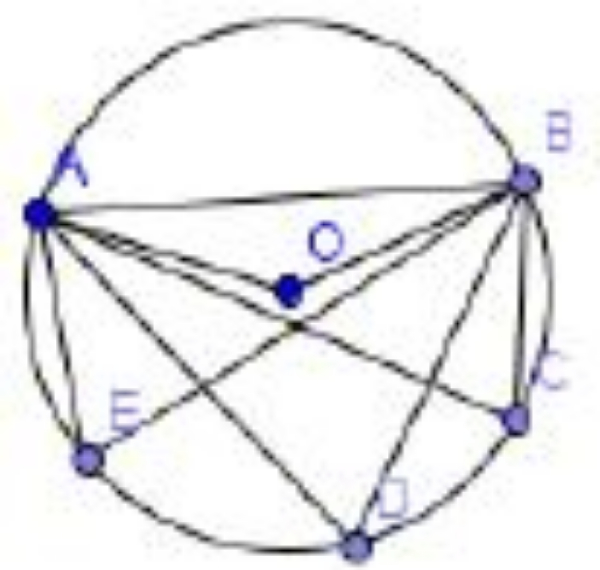
Titik O adalah titik pusat lingkaran. Diketahui sudut ACB + sudut ADB + sudut AEB = 234o. Tentukan besar sudut ACB!
Matematika
Level 8
Geometri
Lingkaran
Diantara titik berikut yang mempunyai jarak 8 satuan terhadap sumbu-y adalah?
Matematika
Level 8
Geometri
Koordinat Kartesius
Syarat informasi yang layak diangkat menjadi sebuah berita adalah memiliki sifat ....
Bahasa Indonesia
Level 8
Menulis
Teks Berita
Simpulan Isi Berita
Kinan — drive — patient — all my friends.
The correct superlative adverb based on the clues is ...
Bahasa Inggris
Level 8
Bahasa Inggris
Comparisons of people or things
Degrees of Comparison of Adverbs
Perhatikanlah letak kelima titik pada bidang koordinat berikut :

Titik yang memiliki jarak satuan dari titik K adalah?
Matematika
Level 8
Geometri
Koordinat Kartesius
Koordinat Posisi Suatu Benda
Perhatikan kalimat puisi bermajas di bawah ini!
1) Oh Diana, kembang desa yang memesona
2) Gadis cantik penebar keramahan
3) Menjadi buah bibir masyarakat sejak lama
4) Diana, diana, diana, siapa tidak mendambamu
Kalimat puisi di atas yang mengandung majas metafora adalah kalimat bernomor ....
Bahasa Indonesia
Level 8
Menulis
Puisi
Unsur-unsur puisi
Agar iklan menarik, maka harus diperhatikan hal berikut, kecuali ....
Bahasa Indonesia
Level 8
Menulis
Iklan, Slogan, Poster
Pola penyajian dan Kebahasaan Iklan, Slogan, Poster
Look at the table below.
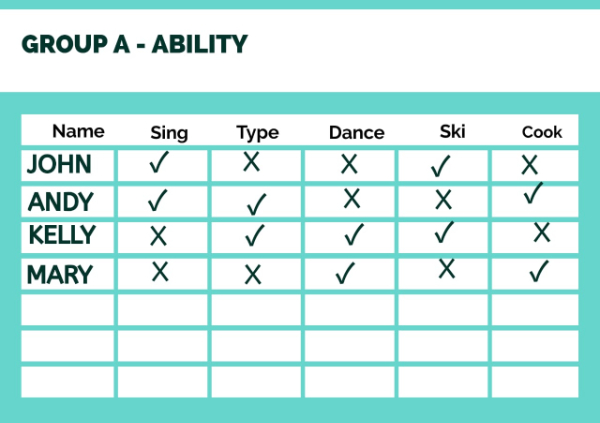
Source: canva.com
Make sentences with 'can' or 'can't' with the verbs in the brackets and join them with 'and' or 'but.'
A. Kelly (cook/dance)
B. Andy (sing/type)
C. John (cook/ski)
Which one is the most suitable statement for point A?
Bahasa Inggris
Level 8
Bahasa Inggris
Interaction among students inside and outside classrooms
Expressions of Explaining Abilities
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Dalam percobaan pengetosan dua koin, banyaknya ruang sampel yang terjadi yaitu ....
Luas daerah yang berwarna merah adalah ... cm2. ( Gunakan )
Perhatikan gambar berikut!
Titik O adalah titik pusat lingkaran. Diketahui sudut ACB + sudut ADB + sudut AEB = 234o. Tentukan besar sudut ACB!
Diantara titik berikut yang mempunyai jarak 8 satuan terhadap sumbu-y adalah?
Syarat informasi yang layak diangkat menjadi sebuah berita adalah memiliki sifat ....
Kinan — drive — patient — all my friends.
The correct superlative adverb based on the clues is ...
Perhatikanlah letak kelima titik pada bidang koordinat berikut :
Titik yang memiliki jarak satuan dari titik K adalah?
Perhatikan kalimat puisi bermajas di bawah ini!
1) Oh Diana, kembang desa yang memesona
2) Gadis cantik penebar keramahan
3) Menjadi buah bibir masyarakat sejak lama
4) Diana, diana, diana, siapa tidak mendambamu
Kalimat puisi di atas yang mengandung majas metafora adalah kalimat bernomor ....
Agar iklan menarik, maka harus diperhatikan hal berikut, kecuali ....
Look at the table below.
Source: canva.com
Make sentences with 'can' or 'can't' with the verbs in the brackets and join them with 'and' or 'but.'
A. Kelly (cook/dance)
B. Andy (sing/type)
C. John (cook/ski)
Which one is the most suitable statement for point A?