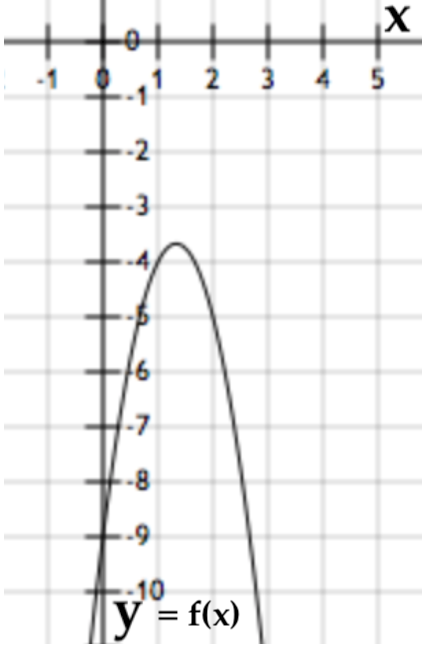
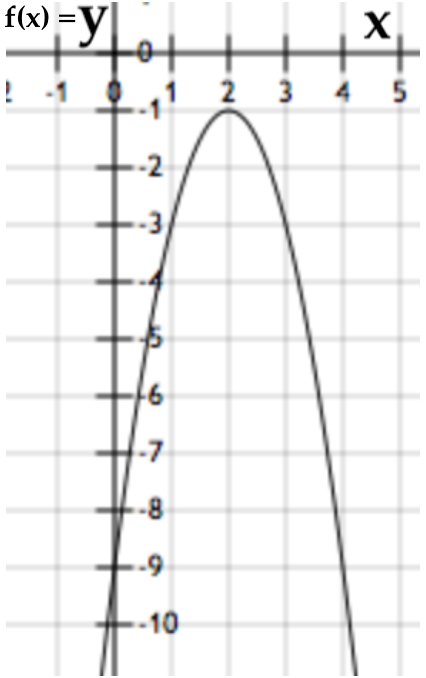
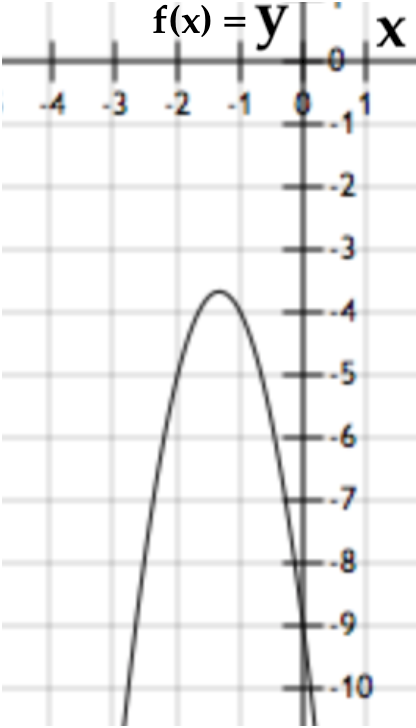
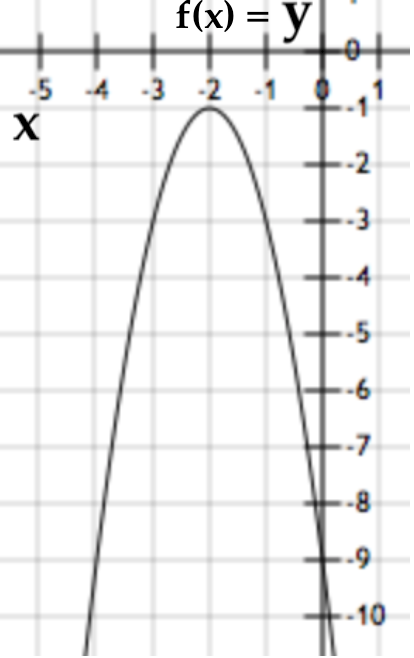
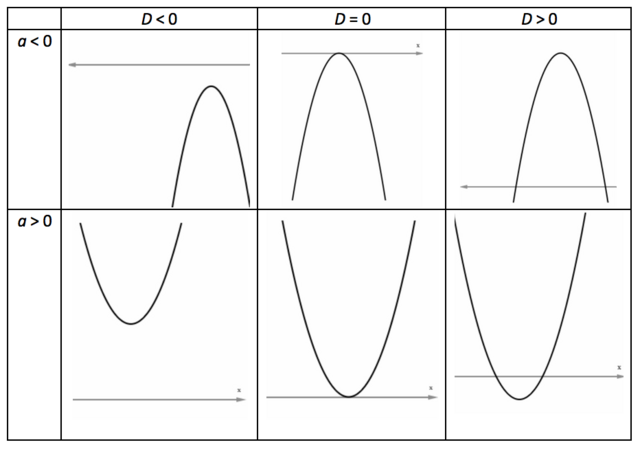
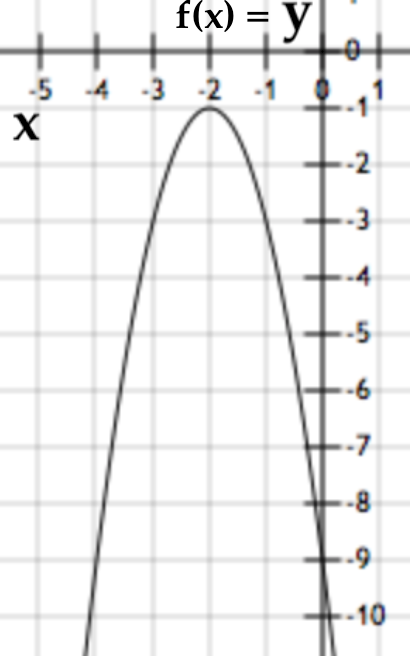
Bank Soal Matematika SMP Nilai dan Grafik Fungsi Kuadrat
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Bagaimanakah cara menyamakan penyebut untuk operasi berikut:
Matematika
Level 5
Bilangan
Operasi Hitung Pecahan
Operasi Hitung Pecahan Biasa dan Campuran
Kelas V
Kurikulum 2013
K13
Matematika
Luna menaiki kereta api dari Semarang menuju Jakarta. Ia berangkat pukul 09.15 dengan kecepatan rata-rata 70 km/jam. Jarak kota Semarang - Jakarta pada peta berskala 1 : 2.000.000 adalah 14 cm. Pukul berapa Luna tiba di Jakarta?
Matematika
Level 5
Geometri
Perbandingan Dua Besaran
Kecepatan
Kelas V
Kurikulum 2013
K13
Matematika

Andi mengikuti lomba menulis cerpen dalam iklan tersebut. Jika Andi berhasil menjadi juara II, hadiah yang berhasil didapatkan Andi adalah sertifikat dan uang sebesar ....
Bahasa Indonesia
Level 5
Membaca
Iklan
Identifikasi Informasi
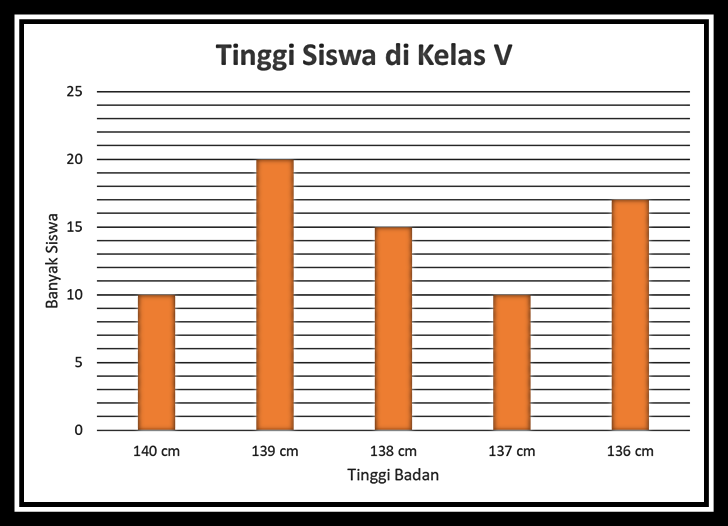
Berdasarkan diagram di atas, berapakah jumlah siswa yang memiliki tinggi 136 cm?
Matematika
Level 5,16
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Asesmen Kompetensi Minimum
Personal
AKM
Data dan Ketidakpastian
Numerasi
Mengambil/Memperoleh
Level 3
Diagram di bawah berisikan fluktuasi harga bensin dari bulan Januari hingga bulan Juni.
Berdasarkan diagram di atas, harga bensin mencapai titik tertingginya pada bulan....
Matematika
Level 5
Statistika
Pengumpulan dan Penyajian Data
Membaca Data
Diagram Garis
Diagram
Kelas V
Kurikulum 2013
K13
Matematika
Sebuah penampung air berbentuk balok memiliki volume 20.000 liter. Jika luas alas penampang air tersebut adalah 2,5 m2, maka tinggi penampang air tersebut ... m
Matematika
Level 5
Geometri
Balok dan Kubus
Volume Balok dan Kubus
Kelas V
Kurikulum 2013
K13
Matematika
Read the conversation below.

Source: games4esl.com
What are they doing?
Bahasa Inggris
Level 5
Bahasa Inggris
Friendship
Greeting & Leave Taking
Kelas V
Kurikulum 2013
K13
Bacalah teks berikut!
Adat istiadat merupakan suatu sistem norma atau tata kelakuan yang tumbuh, berkembang, dan dijunjung tinggi oleh masyarakat secara turun-temurun. Adat istiadat juga merupakan kebiasaan sosial yang sejak lama telah ada di masyarakat dan bertujuan untuk mengatur tata tertib dalam masyarakat tersebut.
Keberagaman budaya menjadikan adat istiadat beragam pula. Adat istiadat terbentuk sesuai dengan kebiasaan masyarakat setempat. Setiap suku yang ada di Indonesia memiliki adat istiadat yang berbeda. Sebagai contoh, tradisi masyarakat Jawa berbeda dengan masyarakat NTT, Bali, maupun Papua. Adat istiadat memiliki aturan khusus yang mengikat masyarakat. Adat istiadat memiliki nilai budaya yang luhur, bersifat mengikat suatu kelompok masyarakat yang tinggal di daerah tertentu, dan memiliki sistem hukum yang tegas bagi seluruh masyarakat.
Meskipun setiap daerah memiliki adat istiadatnya masing-masing, namun Indonesia harus tetap hidup rukun dan damai. Saling menghormati antar suku dan budaya seperti semboyan Bangsa Indonesia yaitu Bhinneka Tunggal Ika, yang artinya berbeda-beda tetapi tetap satu. Perbedaan juga menjadi sebuah kekuatan sehingga memperkaya sifat budaya bangsa Indonesia serta persatuan dan kesatuan bangsa.
Topik yang dibahas pada paragraf ketiga adalah ....
Bahasa Indonesia
Level 5
Membaca
Teks Eksplanasi
Informasi Penting dalam Teks
Berikut yang merupakan contoh surat undangan setengah resmi adalah ....
Bahasa Indonesia
Level 5
Membaca
Surat Undangan
Identifikasi Surat Undangan
Pulau di Indonesia yang termasuk dalam 5 pulau terbesar di dunia adalah ....
IPS
Level 5
Geografi
Karakteristik Geografi Wilayah Indonesia
Karakteristik Geografis
Kelas V
Kurikulum 2013
K13
IPS
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Bagaimanakah cara menyamakan penyebut untuk operasi berikut:
Luna menaiki kereta api dari Semarang menuju Jakarta. Ia berangkat pukul 09.15 dengan kecepatan rata-rata 70 km/jam. Jarak kota Semarang - Jakarta pada peta berskala 1 : 2.000.000 adalah 14 cm. Pukul berapa Luna tiba di Jakarta?
Andi mengikuti lomba menulis cerpen dalam iklan tersebut. Jika Andi berhasil menjadi juara II, hadiah yang berhasil didapatkan Andi adalah sertifikat dan uang sebesar ....
Berdasarkan diagram di atas, berapakah jumlah siswa yang memiliki tinggi 136 cm?
Diagram di bawah berisikan fluktuasi harga bensin dari bulan Januari hingga bulan Juni.
Berdasarkan diagram di atas, harga bensin mencapai titik tertingginya pada bulan....
Sebuah penampung air berbentuk balok memiliki volume 20.000 liter. Jika luas alas penampang air tersebut adalah 2,5 m2, maka tinggi penampang air tersebut ... m
Read the conversation below.

Source: games4esl.com
What are they doing?
Bacalah teks berikut!
Adat istiadat merupakan suatu sistem norma atau tata kelakuan yang tumbuh, berkembang, dan dijunjung tinggi oleh masyarakat secara turun-temurun. Adat istiadat juga merupakan kebiasaan sosial yang sejak lama telah ada di masyarakat dan bertujuan untuk mengatur tata tertib dalam masyarakat tersebut.
Keberagaman budaya menjadikan adat istiadat beragam pula. Adat istiadat terbentuk sesuai dengan kebiasaan masyarakat setempat. Setiap suku yang ada di Indonesia memiliki adat istiadat yang berbeda. Sebagai contoh, tradisi masyarakat Jawa berbeda dengan masyarakat NTT, Bali, maupun Papua. Adat istiadat memiliki aturan khusus yang mengikat masyarakat. Adat istiadat memiliki nilai budaya yang luhur, bersifat mengikat suatu kelompok masyarakat yang tinggal di daerah tertentu, dan memiliki sistem hukum yang tegas bagi seluruh masyarakat.
Meskipun setiap daerah memiliki adat istiadatnya masing-masing, namun Indonesia harus tetap hidup rukun dan damai. Saling menghormati antar suku dan budaya seperti semboyan Bangsa Indonesia yaitu Bhinneka Tunggal Ika, yang artinya berbeda-beda tetapi tetap satu. Perbedaan juga menjadi sebuah kekuatan sehingga memperkaya sifat budaya bangsa Indonesia serta persatuan dan kesatuan bangsa.
Topik yang dibahas pada paragraf ketiga adalah ....
Berikut yang merupakan contoh surat undangan setengah resmi adalah ....
Pulau di Indonesia yang termasuk dalam 5 pulau terbesar di dunia adalah ....