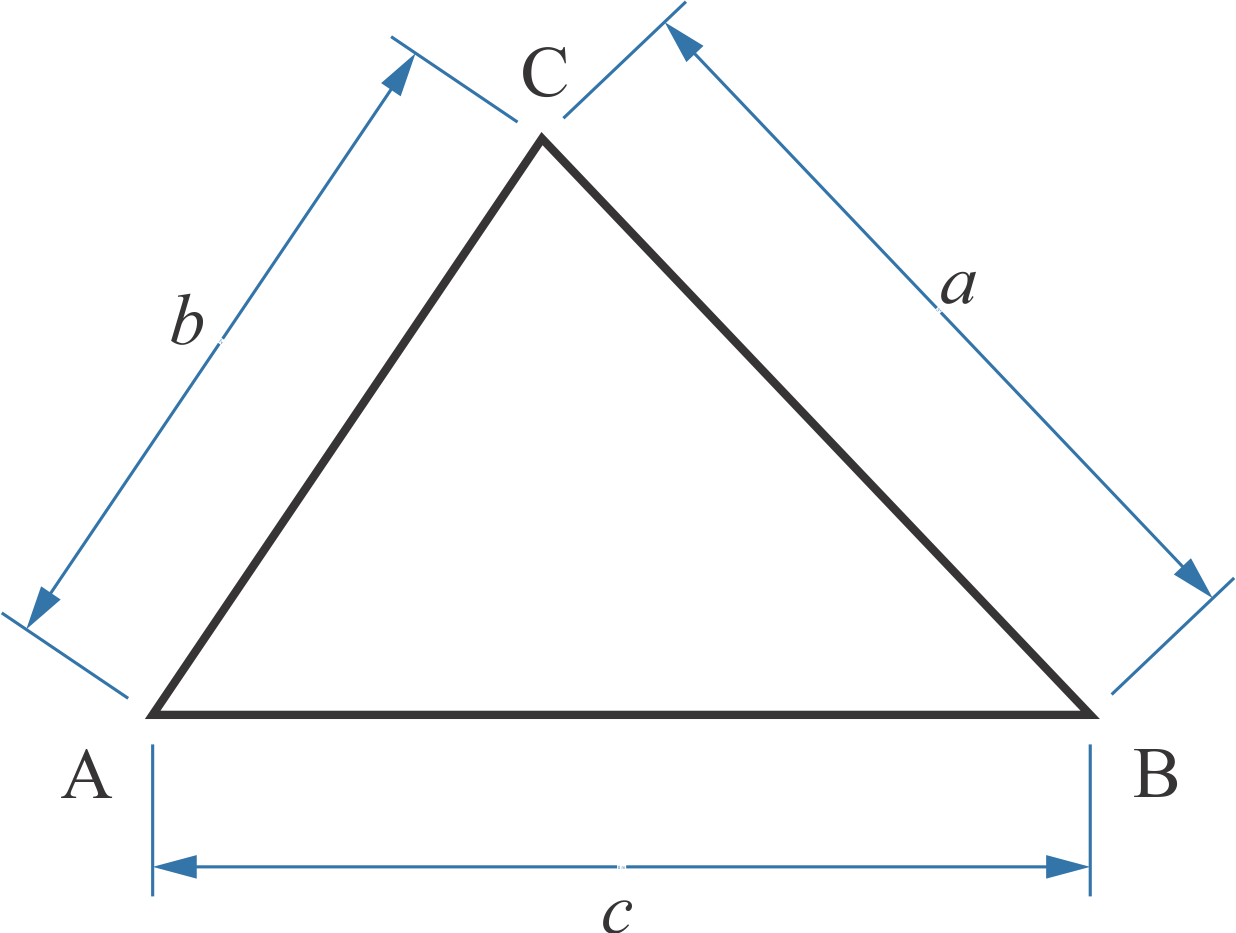
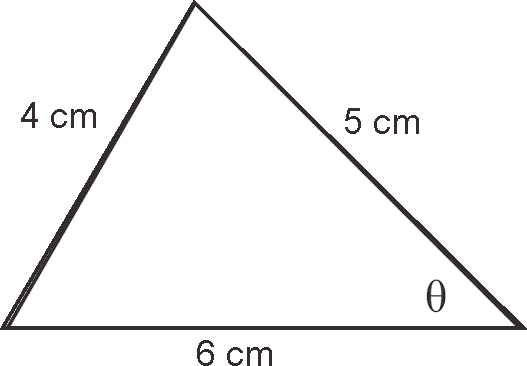
Bank Soal Matematika SMA Aturan Cosinus
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
Biologi
Level 10
Biologi
Ruang Lingkup Biologi
Objek dan Permasalahan Biologi
Kelas X
Kurikulum 2013
K13
To support her friend, Amy gives a complement to Kelly by saying ...
Bahasa Inggris
Level 10
Congratulating and Complimenting
Expressions of Congratulating and Complimenting
Kelas X
Kurikulum 2013
K13
Bahasa Inggris
Perhatikan gambar berikut!

Sumber: seputarilmu.com
Ketiga spesies di atas termasuk dalam kelompok yang sama, yaitu pada tingkatan takson ....
Biologi
Level 10
Biologi
Keanekaragaman Hayati
Klasifikasi Makhluk Hidup
Kelas X
Kurikulum 2013
K13
Sebagai seorang peneliti sains termasuk fisika, memiliki sikap yang baik saja tidaklah cukup. Peneliti juga memerlukan kecakapan ilmiah yang harus dikuasai. Berikut ini yang bukan kecakapan ilmiah untuk menjadi peneliti sains adalah ....
Fisika
Level 10
Fisika
Hakikat Fisika dan Keselamatan Kerja Laboratorium
Hakikat dan Peran Fisika
Kelas X
Kurikulum 2013
K13
Selang ( ) dillukiskan oleh garis bilangan ....
Matematika
Level 10
Aljabar
Persamaan dan Pertidaksamaan Nilai Mutlak
Pertidaksamaan Linear Satu Variabel
Kelas X
Kurikulum 2013
K13
Matematika Wajib
Jumlah nilai x yang memenuhi sistem persamaan
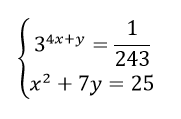
adalah....
Matematika
Level 10,10
Aljabar
Fungsi, Persamaan, dan Pertidaksamaan Eksponensial
Kurikulum Merdeka
KurMer
Kelas X
Kurikulum 2013
K13
Matematika Peminatan
Sebelum menjadi makanan umum, bahan utama sate lilit adalah ….
Bahasa Indonesia
Level 10
Teks Laporan Hasil Observasi
Interpretasi dan Analisis Teks Laporan Hasil Observasi
Kelas X
Kurikulum 2013
K13
Bahasa Indonesia
Penyebaran penyakir pada tembakau di bawah ini dilakukan dengan cara .... (Pilih semua jawaban yang benar!)

sumber: pak.pandani.web.id
Biologi
Level 10
Biologi
Virus
Klasifikasi dan Peranan Virus dalam Kehidupan
Kelas X
Kurikulum 2013
K13
Pada jaring-jaring makanan di bawah ini, organisme X berperan sebagai ....
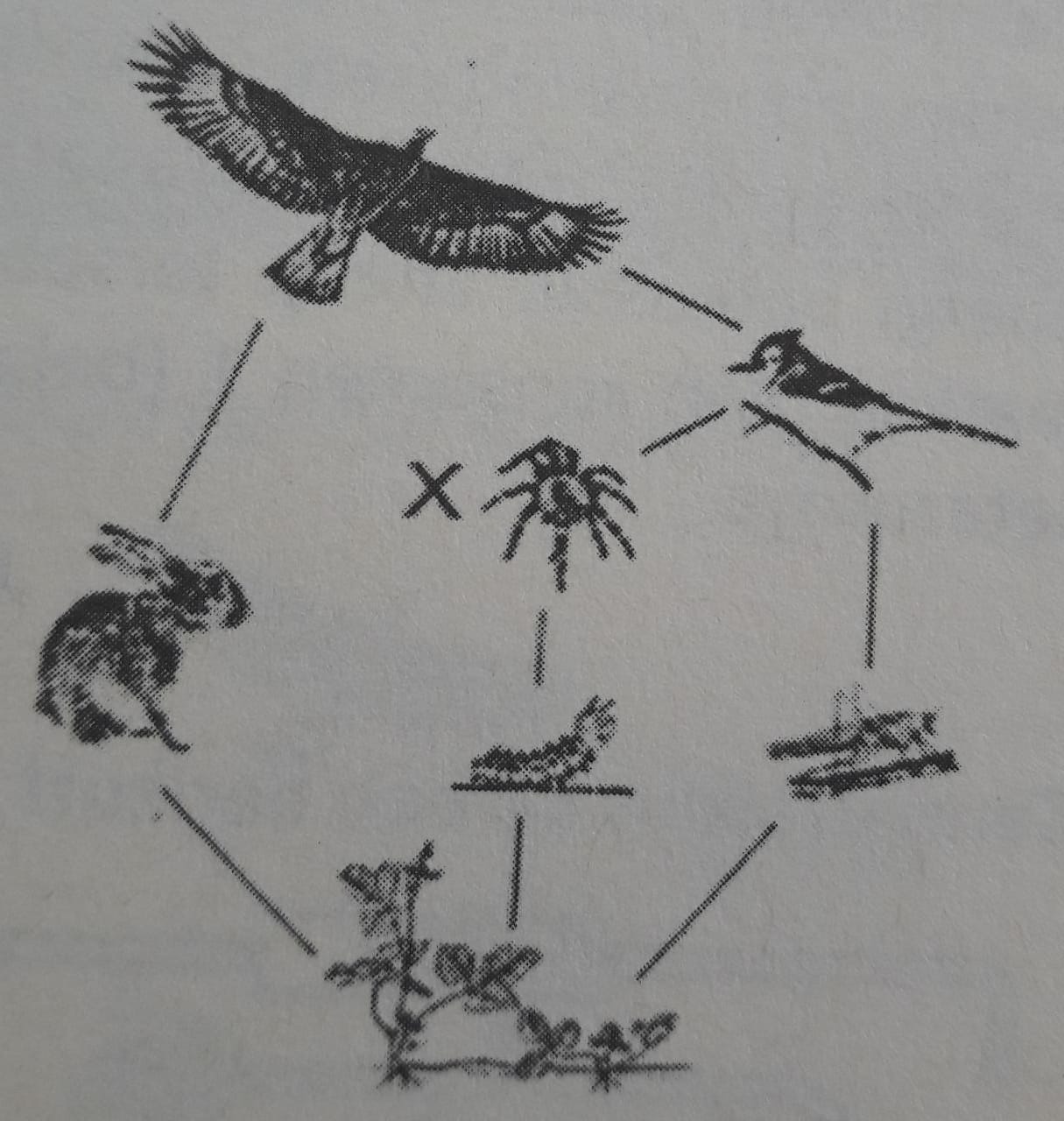
(UN 2014)
Biologi
Level 10
Biologi
Ekologi
Aliran Energi dan Piramida Ekologi
Kelas X
Kurikulum 2013
K13
Limbah seperti gambar di bawah ini masih bisa dimanfaatkan menjadi ....

sumber: sumbarprov.go.id
Biologi
Level 10
Biologi
Perubahan dan Pelestarian Lingkungan Hidup
Bahan Pencemar dan Penanganan Limbah
Kelas X
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Populasi tikus di sawah dapat terpengaruh oleh populasi ular. Hal ini menunjukkan permasalahan biologi pada tingkat ....
To support her friend, Amy gives a complement to Kelly by saying ...
Perhatikan gambar berikut!
Sumber: seputarilmu.com
Ketiga spesies di atas termasuk dalam kelompok yang sama, yaitu pada tingkatan takson ....
Sebagai seorang peneliti sains termasuk fisika, memiliki sikap yang baik saja tidaklah cukup. Peneliti juga memerlukan kecakapan ilmiah yang harus dikuasai. Berikut ini yang bukan kecakapan ilmiah untuk menjadi peneliti sains adalah ....
Selang ( ) dillukiskan oleh garis bilangan ....
Jumlah nilai x yang memenuhi sistem persamaan
adalah....
Sebelum menjadi makanan umum, bahan utama sate lilit adalah ….
Penyebaran penyakir pada tembakau di bawah ini dilakukan dengan cara .... (Pilih semua jawaban yang benar!)

sumber: pak.pandani.web.id
Pada jaring-jaring makanan di bawah ini, organisme X berperan sebagai ....

(UN 2014)
Limbah seperti gambar di bawah ini masih bisa dimanfaatkan menjadi ....

sumber: sumbarprov.go.id