Bank Soal Matematika SMA Aplikasi Integral
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
The correct word to fill in the sentence number (III) is ....
Bahasa Inggris
Level 12
Bahasa Inggris
News Item
News Item
Dewa melakukan praktikum dengan menggunakan kecambah. Kecambah diletakan pada posisi miring lalu didiamkan tumbuh. Setelah beberapa hari, Dewa datang untuk mengukur pertumbuhan tanaman, namun Dewa menemukan bahwa tunas kecambah tumbuh membengkok ke arah atas sedangkan akar tumbuh membengkok ke arah bawah. Mengapa hal ini terjadi?
Biologi
Level 12
Biologi
Pertumbuhan dan Perkembangan Makhluk Hidup
Pertumbuhan dan Perkembangan pada Tumbuhan
Gambar berikut menunjukkan sebuah gedung yang berukuran m m. Tinggi langit-langit dari lantai m, tinggi atap dari lantai m.
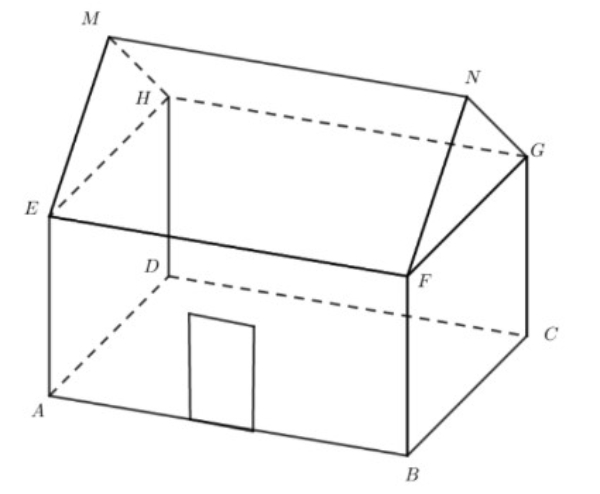
Jika dan , besar sudut antara atap dan langit-langit adalah ....
Matematika
Level 12
Geometri
Dimensi Tiga (Geometri Ruang)
Memecahkan Masalah Bangun Ruang
Ask for a service using the available phrase.

carry the packages
Bahasa Inggris
Level 12
Bahasa Inggris
Services
Modals
Salah satu tokoh penting di kabinet Djuanda, gambar tokohnya diabadikan oleh pemerintah Indonesia dalam uang kertas pecahan ....
Sejarah Indonesia
Level 12
Kehidupan Politik dan Ekonomi Indonesia Masa Awal Kemerdekaan, Demokrasi Terpimpin, dan Demokrasi Liberal
Perkembangan Politik dan Ekonomi Indonesia (1945-1965)
Berdasarkan diagram P-T di bawah ini, yang menunjukkan penurunan titik beku larutan adalah ….

Kimia
Level 12
Sifat Koligatif Larutan
Penurunan Titik Beku
Sebuah lampu pijar dengan spesifikasi 60 W pada 220 volt, dipasang pada suatu sumber potensial sebesar 110 volt. Daya yang diperlukan lampu adalah ....
Fisika
Level 12
Fisika
Rangkaian Arus Searah
Daya dan Energi Listrik
Perhatikan faktor-faktor berikut!
- Panjang gelombang cahaya
- Intensitas cahaya
- Zat inhibitor
- Suhu
- Zat hasil (produk)
Faktor lingkungan yang memengaruhi fotosintesis adalah ....
Biologi
Level 12
Biologi
Enzim dan Metabolisme Sel
Anabolisme (Fotosintesis)
Nilai
Matematika
Level 12
Trigonometri
Limit Fungsi Trigonometri
Perhatikan gambar berikut!
Sumber: www.wikipedia.org
Tokoh tersebut adalah Sultan Syarif Kasim II, Sultan Siak (Riau) yang berjasa besar dalam upaya mempertahankan kemerdekaan dan menghadapi ancaman disintegrasi bangsa.
Lantas, bagaimanakah peran Sultan Syarif Kasim II upayanya tersebut?
Sejarah Indonesia
Level 12
Upaya Bangsa Indonesia Menghadapi Ancaman Disintegrasi Bangsa
Tokoh Perjuangan Mempertahankan Integrasi Bangsa
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
The correct word to fill in the sentence number (III) is ....
Dewa melakukan praktikum dengan menggunakan kecambah. Kecambah diletakan pada posisi miring lalu didiamkan tumbuh. Setelah beberapa hari, Dewa datang untuk mengukur pertumbuhan tanaman, namun Dewa menemukan bahwa tunas kecambah tumbuh membengkok ke arah atas sedangkan akar tumbuh membengkok ke arah bawah. Mengapa hal ini terjadi?
Gambar berikut menunjukkan sebuah gedung yang berukuran m m. Tinggi langit-langit dari lantai m, tinggi atap dari lantai m.
Jika dan , besar sudut antara atap dan langit-langit adalah ....
Ask for a service using the available phrase.

carry the packages
Salah satu tokoh penting di kabinet Djuanda, gambar tokohnya diabadikan oleh pemerintah Indonesia dalam uang kertas pecahan ....
Berdasarkan diagram P-T di bawah ini, yang menunjukkan penurunan titik beku larutan adalah ….
Sebuah lampu pijar dengan spesifikasi 60 W pada 220 volt, dipasang pada suatu sumber potensial sebesar 110 volt. Daya yang diperlukan lampu adalah ....
Perhatikan faktor-faktor berikut!
- Panjang gelombang cahaya
- Intensitas cahaya
- Zat inhibitor
- Suhu
- Zat hasil (produk)
Faktor lingkungan yang memengaruhi fotosintesis adalah ....
Nilai
Perhatikan gambar berikut!
Sumber: www.wikipedia.org
Tokoh tersebut adalah Sultan Syarif Kasim II, Sultan Siak (Riau) yang berjasa besar dalam upaya mempertahankan kemerdekaan dan menghadapi ancaman disintegrasi bangsa.
Lantas, bagaimanakah peran Sultan Syarif Kasim II upayanya tersebut?




