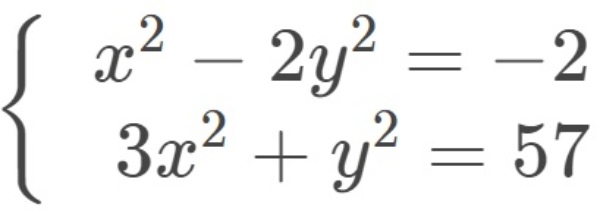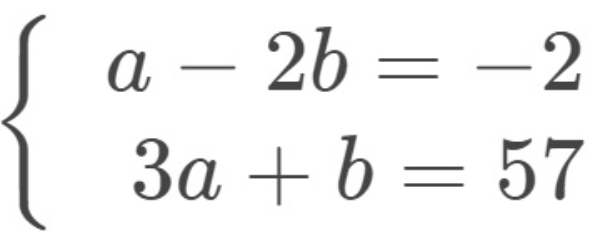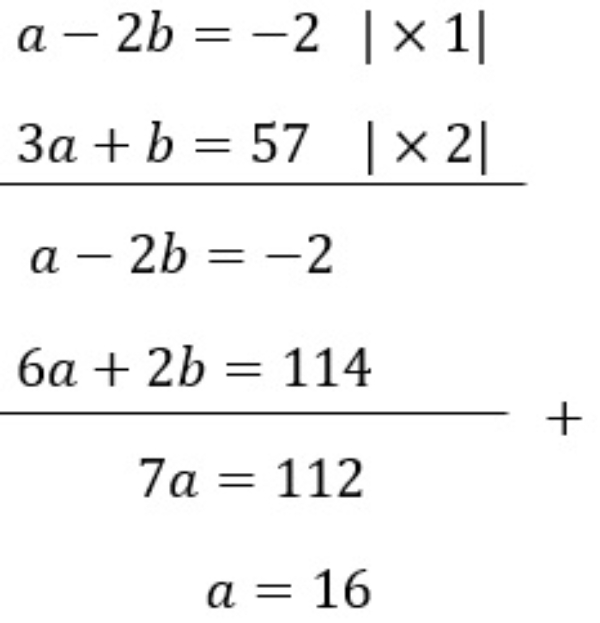Bank Soal Matematika SMA Sistem Persamaan Linear Dua Variabel
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
= ...
Pecahan tersebut senilai dengan ...
Matematika
Level 4
Bilangan
Pecahan
Pecahan Senilai
Rumus luas jajar genjang yaitu …
Matematika
Level 5,6
Geometri
Bangun Datar
Ulasan Novel Aku, Meps, dan Beps
"Aku panggil emakku 'Meps' dan bapakku 'Beps'. Kenapa? Hihihi, aku nggak tahu. Tahu-tahu aku sudah panggil mereka begitu. Meps rambutnya pendek banget. Kata Beps, setiap minggu Meps mesti cukur. Kalau tidak, kesaktiannya hilang. Apa kesaktian Meps? Nanti aku ceritakan!"

Sampul novel Aku, Meps, dan Beps karya Reda Gaudiamo dan Soca Sobitha, diterbitkan oleh Post Press
Buku ini merupakan hasil tulisan kolaborasi antara Reda Gaudiamo dan Soca Sobitha, seorang ibu dan anaknya. Buku yang bercerita tentang kehidupan sederhana dalam keluarga perkotaan ini sangat cocok dibaca oleh anak-anak.
Buku ini berisi kisah sederhana, tetapi menghibur dan kocak dari seorang anak kecil. Tokoh "aku" dalam buku ini menceritakan perasaannya ketika mandi hujan, perasaan suka dan benci pergi ke sekolah, mempunyai binatang di rumah, dan sebagainya.
Buku ini memiliki keistimewaan dibanding buku cerita anak lainnya karena dituturkan dari sudut pandang seorang anak kecil. Bahasa dalam buku ini juga memakai gaya polos dan lugu.
Bagian inspiratif dari buku ini adalah sifat dari tokoh "aku". Tokoh "aku'" digambarkan mempunyai rasa ingin tahu yang tinggi, aktif bertanya, dan percaya diri.
(Sumber: goodreads.com, dengan penyesuaian)
Berdasarkan ulasan buku di atas, tokoh yang mempunyai rambut pendek adalah ....
Bahasa Indonesia
Level 4
Membaca
Buku Sastra
Ulasan Buku Sastra

Source: freepik.com
Put the words in the correct order to make a good sentence.
chef / is / a / she
The correct order is ...
Bahasa Inggris
Level 4
Bahasa Inggris
Jobs
Simple Present Tense
Adik mempunyai setumpuk kartu. Di belakang kartu itu terdapat bilangan dari 100 sampai 200. Jika adik hanya mengambil kartu dengan bilangan yang habis dibagi 7, maka jumlah kartu yang diambil adik ada ... buah.
Matematika
Level 4
Bilangan
Faktor dan Kelipatan
Kelipatan Bilangan
Sebuah taman mempunyai panjang sisi 14 m. Luas taman tersebut adalah ... m2
Matematika
Level 4
Geometri
Bangun Datar
Keliling dan Luas Persegi
Di sebuah mall terpasang lampu hias. Lampu biru menyala setiap 12 detik, kemudian padam. Lampu merah menyala setiap 16 detik kemudian padam. Lampu kuning menyala setiap 18 detik kemudian padam. maka ketiga lampu akan menyala secara bersamaan pada detik ke ...
Matematika
Level 4
Bilangan
FPB dan KPK
KPK
Reza sedang mengerjakan ujian Matematika sebanyak 40 soal.
3 soal tidak dikerjakan Reza karena susah.
Banyak soal yang dijawab benar oleh Reza 11 kali banyak soal yang tidak dia jawab.
Soal yang dijawab salah oleh Reza adalah … soal.
Bahasa Indonesia
Level 3
Membaca
Teks Fiksi-Tokoh Cerita
Dongeng
(i) Sudut yang 2 kali lebih besar dari komplemen suatu sudut sebesar 21o
(ii) Sudut suplemen dari suatu sudut yang perbandingannya dengan penyikunya adalah 1:1
(iii) Sudut yang besarnya kali suplemennya
(iv) Sudut pelurus dari komplemen suatu sudut sebesar 46o
Urutan besar sudut di atas dari yang terbesar adalah ....
Matematika
Level 4
Geometri
Garis dan Sudut
Sudut
Perhatikan tabel berikut.

Kelas manakah yang mempunyai jumlah murid paling sedikit?
Matematika
Level 4
Statistika
Bentuk Diagram
Membaca Diagram
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
= ...
Pecahan tersebut senilai dengan ...
Rumus luas jajar genjang yaitu …
Ulasan Novel Aku, Meps, dan Beps
"Aku panggil emakku 'Meps' dan bapakku 'Beps'. Kenapa? Hihihi, aku nggak tahu. Tahu-tahu aku sudah panggil mereka begitu. Meps rambutnya pendek banget. Kata Beps, setiap minggu Meps mesti cukur. Kalau tidak, kesaktiannya hilang. Apa kesaktian Meps? Nanti aku ceritakan!"
Sampul novel Aku, Meps, dan Beps karya Reda Gaudiamo dan Soca Sobitha, diterbitkan oleh Post Press
Buku ini merupakan hasil tulisan kolaborasi antara Reda Gaudiamo dan Soca Sobitha, seorang ibu dan anaknya. Buku yang bercerita tentang kehidupan sederhana dalam keluarga perkotaan ini sangat cocok dibaca oleh anak-anak.
Buku ini berisi kisah sederhana, tetapi menghibur dan kocak dari seorang anak kecil. Tokoh "aku" dalam buku ini menceritakan perasaannya ketika mandi hujan, perasaan suka dan benci pergi ke sekolah, mempunyai binatang di rumah, dan sebagainya.
Buku ini memiliki keistimewaan dibanding buku cerita anak lainnya karena dituturkan dari sudut pandang seorang anak kecil. Bahasa dalam buku ini juga memakai gaya polos dan lugu.
Bagian inspiratif dari buku ini adalah sifat dari tokoh "aku". Tokoh "aku'" digambarkan mempunyai rasa ingin tahu yang tinggi, aktif bertanya, dan percaya diri.
(Sumber: goodreads.com, dengan penyesuaian)
Berdasarkan ulasan buku di atas, tokoh yang mempunyai rambut pendek adalah ....
Source: freepik.com
Put the words in the correct order to make a good sentence.
chef / is / a / she
The correct order is ...
Adik mempunyai setumpuk kartu. Di belakang kartu itu terdapat bilangan dari 100 sampai 200. Jika adik hanya mengambil kartu dengan bilangan yang habis dibagi 7, maka jumlah kartu yang diambil adik ada ... buah.
Sebuah taman mempunyai panjang sisi 14 m. Luas taman tersebut adalah ... m2
Di sebuah mall terpasang lampu hias. Lampu biru menyala setiap 12 detik, kemudian padam. Lampu merah menyala setiap 16 detik kemudian padam. Lampu kuning menyala setiap 18 detik kemudian padam. maka ketiga lampu akan menyala secara bersamaan pada detik ke ...
Reza sedang mengerjakan ujian Matematika sebanyak 40 soal.
3 soal tidak dikerjakan Reza karena susah.
Banyak soal yang dijawab benar oleh Reza 11 kali banyak soal yang tidak dia jawab.
Soal yang dijawab salah oleh Reza adalah … soal.
(i) Sudut yang 2 kali lebih besar dari komplemen suatu sudut sebesar 21o
(ii) Sudut suplemen dari suatu sudut yang perbandingannya dengan penyikunya adalah 1:1
(iii) Sudut yang besarnya kali suplemennya
(iv) Sudut pelurus dari komplemen suatu sudut sebesar 46o
Urutan besar sudut di atas dari yang terbesar adalah ....
Perhatikan tabel berikut.
Kelas manakah yang mempunyai jumlah murid paling sedikit?