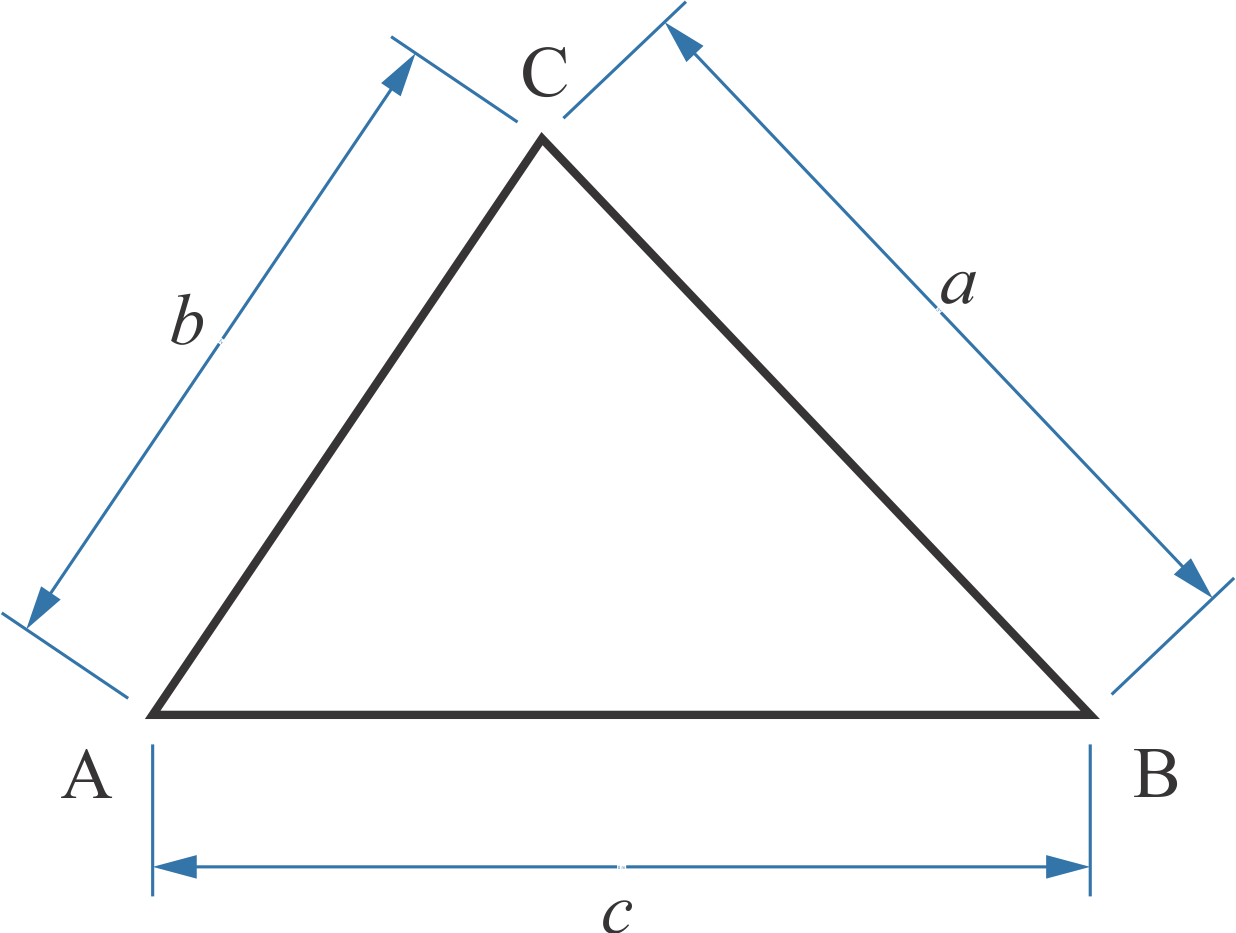
Bank Soal Matematika SMA Aturan Sinus
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Jenis polisakarida yang terdapat pada sel otot dan hati hewan serta berperan sebagai cadangan makanan adalah ....
Biologi
Level 11
Biologi
Sel
Penemuan, Tipe, Ukuran, dan Komponen Kimiawi Sel
The one who offers help is ....
Bahasa Inggris
Level 11
Good Advice
Making Offers
Lingkaran merupakan bayangan dari lingkaran yang ditranslasikan oleh 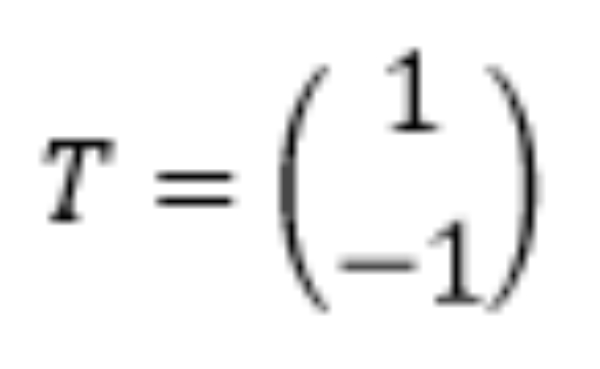 . Persamaan lingkaran adalah ....
. Persamaan lingkaran adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
Diketahui adalah rumus dari
Jika benar untuk , maka ruas kiri menjadi ....
Matematika
Level 11
Logika
Induksi Matematika
Induksi Matematika pada Barisan Bilangan
Salah satu kegunaan senyawa hidrokarbon dalam kehidupan sehari-hari adalah proses pengelasan pada suatu logam. Pada proses pengelasan, digunakan suatu gas dari golongan alkuna yang merupakan hasil reaksi dari kalsium karbida dengan air. Gas yang dimaksud adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Perhatikan gambar berikut.

Poros berada di O dan titik O berada di tengah-tengah batang. Total torsi pada titik O adalah .... (; )
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Dinamika Benda Tegar
Perhatikan data di bawah ini!
- Ukuran partikel
- Luas area
- Suhu
- Jarak
Berdasarkan data di atas, faktor-faktor yang mempengaruhi kecepatan difusi adalah nomor ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Jenis reaksi yang terdapat pada persamaan reaksi berikut adalah ....
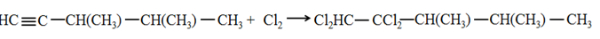
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Terdapat sebuah persamaan trigonometri , maka salah satu nilai dari dapat didefinisikan sebagai ....
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!

Berdasarkan data tersebut, kemungkinan efek rumah kaca terjadi lebih besar di ... dan planet yang memiliki suhu permukaan rata-rata yang lebih rendah adalah ....
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Jenis polisakarida yang terdapat pada sel otot dan hati hewan serta berperan sebagai cadangan makanan adalah ....
The one who offers help is ....
Lingkaran merupakan bayangan dari lingkaran yang ditranslasikan oleh 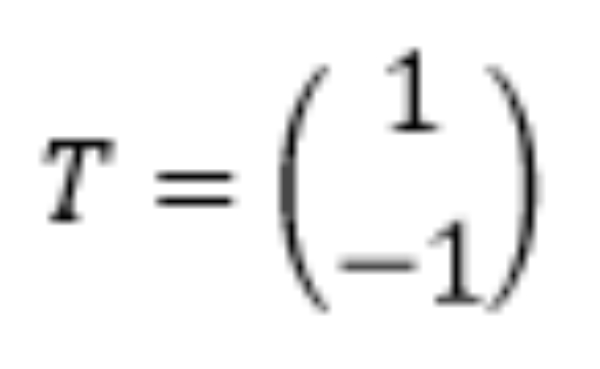
Diketahui adalah rumus dari
Jika benar untuk , maka ruas kiri menjadi ....
Salah satu kegunaan senyawa hidrokarbon dalam kehidupan sehari-hari adalah proses pengelasan pada suatu logam. Pada proses pengelasan, digunakan suatu gas dari golongan alkuna yang merupakan hasil reaksi dari kalsium karbida dengan air. Gas yang dimaksud adalah ....
Perhatikan gambar berikut.
Poros berada di O dan titik O berada di tengah-tengah batang. Total torsi pada titik O adalah .... (; )
Perhatikan data di bawah ini!
- Ukuran partikel
- Luas area
- Suhu
- Jarak
Berdasarkan data di atas, faktor-faktor yang mempengaruhi kecepatan difusi adalah nomor ....
Jenis reaksi yang terdapat pada persamaan reaksi berikut adalah ....
Terdapat sebuah persamaan trigonometri , maka salah satu nilai dari dapat didefinisikan sebagai ....
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
Berdasarkan data tersebut, kemungkinan efek rumah kaca terjadi lebih besar di ... dan planet yang memiliki suhu permukaan rata-rata yang lebih rendah adalah ....