Bank Soal Matematika SMA Induksi Matematika pada Ketidaksamaan
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Nilai y pada persamaan
−5y − 180 = 60 − (−7y) adalah ....
Matematika
Level 7
Aljabar
Persamaan dan Pertidaksamaan Linear Satu Variabel
Persamaan Linear Satu Variabel (PLSV)
(i) (-50)2 -32 + 23 = 0
(ii) -82 : (22)3 = 20
(iii) 73 - 35 = 102
Pernyataan yang tepat adalah ...
Matematika
Level 7
Bilangan
Bilangan dan Operasi Hitung Bilangan
Bilangan Berpangkat
Perhatikan gambar berikut.

Bagian yang diarsir menunjukkan …
Matematika
Level 7
Bilangan
Himpunan
Konsep dan Macam-Macam Himpunan
Perhatikan gambar berikut!
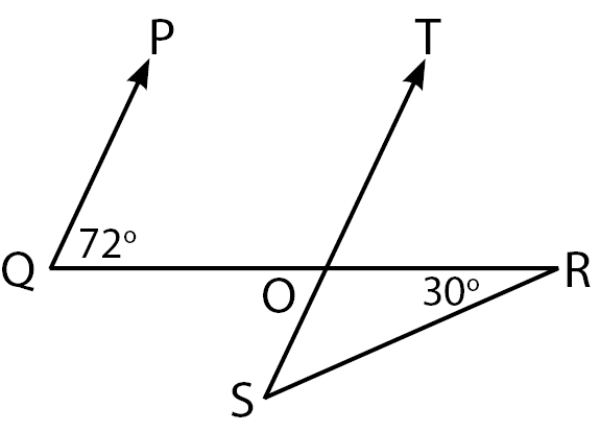
Besar RSO yang memenuhi gambar di atas adalah ....
Matematika
Level 7
Geometri
Garis dan Sudut
Hubungan Antar Sudut
Pernyataan berikut yang termasuk ciri-ciri teks deskripsi adalah ....
Bahasa Indonesia
Level 7
Menulis
Teks Deskripsi
Ciri dan Tujuan Teks Deskripsi
Suku-suku dari bentuk aljabar adalah ….
Matematika
Level 7
Aljabar
Bentuk Aljabar
Konsep Bentuk Aljabar
Berikut ini adalah bagian-bagian surat yang hanya terdapat dalam surat dinas, yaitu ....
Bahasa Indonesia
Level 7
Menulis
Surat Pribadi dan Surat Dinas
Unsur-unsur dan Kebahasaan Surat
Ketika akan membuat komentar terhadap buku maka data buku sebaiknya terletak di ....
Bahasa Indonesia
Level 7
Menulis
Buku Fiksi dan Nonfiksi
Komentar terhadap Buku Fiksi dan Nonfiksi
Adi ingin mengumpulkan data tinggi badan teman-teman di kelasnya. Cara apa yang paling tepat untuk mengumpulkan data tersebut?
Matematika
Level 7
Statistika
Penyajian dan Pengolahan Data
Konsep dan Pengumpulan Data
We say 'What do you do' when we want to know someone's ....
Bahasa Inggris
Level 7
Bahasa Inggris
Describing oneself
Self Introduction
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Nilai y pada persamaan
−5y − 180 = 60 − (−7y) adalah ....
(i) (-50)2 -32 + 23 = 0
(ii) -82 : (22)3 = 20
(iii) 73 - 35 = 102
Pernyataan yang tepat adalah ...
Perhatikan gambar berikut.
Bagian yang diarsir menunjukkan …
Perhatikan gambar berikut!
Besar RSO yang memenuhi gambar di atas adalah ....
Pernyataan berikut yang termasuk ciri-ciri teks deskripsi adalah ....
Suku-suku dari bentuk aljabar adalah ….
Berikut ini adalah bagian-bagian surat yang hanya terdapat dalam surat dinas, yaitu ....
Ketika akan membuat komentar terhadap buku maka data buku sebaiknya terletak di ....
Adi ingin mengumpulkan data tinggi badan teman-teman di kelasnya. Cara apa yang paling tepat untuk mengumpulkan data tersebut?
We say 'What do you do' when we want to know someone's ....



