Bank Soal Matematika SMA Fungsi Trigonometri dan Bilangan Real
Soal
Rangkuman

Bab 5 | Bangun Datar | Matematika | Kelas 4
Selengkapnya



Soal Populer Hari Ini
Kelompok lipid yang terlibat dalam penyusun lapisan kutikula pada permukaan daun tanaman adalah ....
Biologi
Level 11
Biologi
Sel
Penemuan, Tipe, Ukuran, dan Komponen Kimiawi Sel
Kelas XI
Kurikulum 2013
K13
Jika titik ditranslasikan oleh 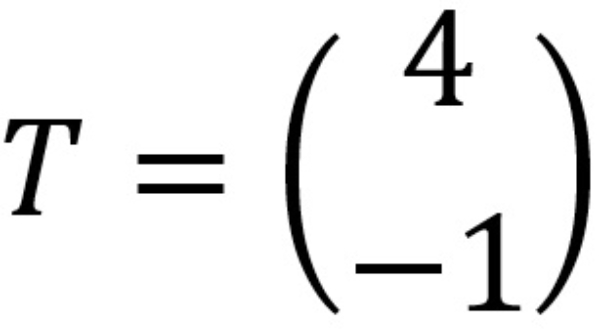 maka bayangan titik adalah ....
maka bayangan titik adalah ....
Matematika
Level 11
Geometri
Transformasi Geometri
Tranlasi
Kelas XI
Kurikulum 2013
K13
Matematika Wajib
Complete the dialogue below.

Renny: I’ve been working since 8 in the morning. Now, I feel tired and hungry.
Dan: ______
Bahasa Inggris
Level 11
Good Advice
Giving Advice or Suggestions
Kelas XI
Kurikulum 2013
K13
Bahasa Inggris
Perhatikan beberapa pernyataan terkait notasi sigma berikut!
-
-
-
-
-
Pernyataan yang benar ditunjukkan oleh nomor ....
Matematika
Level 11
Logika
Induksi Matematika
Notasi Sigma
Kelas XI
Kurikulum 2013
K13
Matematika Wajib
Berikut ini yang bukan merupakan benda yang mengandung senyawa hidrokarbon adalah ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Kelas XI
Kurikulum 2013
K13
Kimia
Perhatikan gambar berikut.
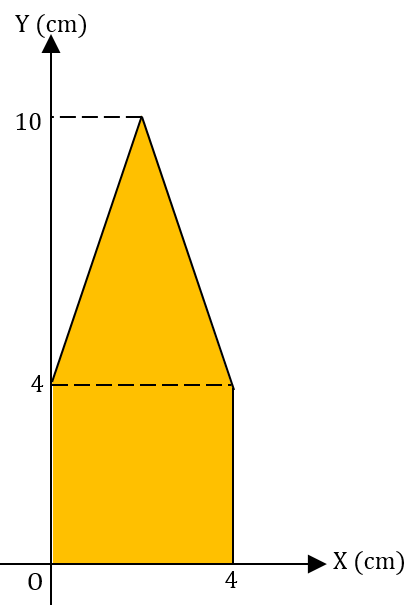
Titik berat bangun tersebut adalah ....
Fisika
Level 11
Fisika
Dinamika dan Keseimbangan Benda Tegar
Titik Berat
Kelas XI
Kurikulum 2013
K13
Membran sel bersifat impermeabel terhadap molekul di bawah ini, kecuali ....
Biologi
Level 11
Biologi
Sel
Mekanisme Transpor Membran Plasma
Kelas XI
Kurikulum 2013
K13
Berdasarkan aturan Markovnikoff, reaksi adisi terhadap 4-metil-2-pentena dengan asam klorida menghasilkan suatu senyawa berupa ....
Kimia
Level 11
Hidrokarbon dan Minyak Bumi
Hidrokarbon
Kelas XI
Kurikulum 2013
K13
Kimia
Himpunan penyelesaian untuk persamaan trigonometri pada interval adalah ....
Matematika
Level 11
Trigonometri
Persamaan Trigonometri
Kelas XI
Kurikulum 2013
K13
Matematika Peminatan
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
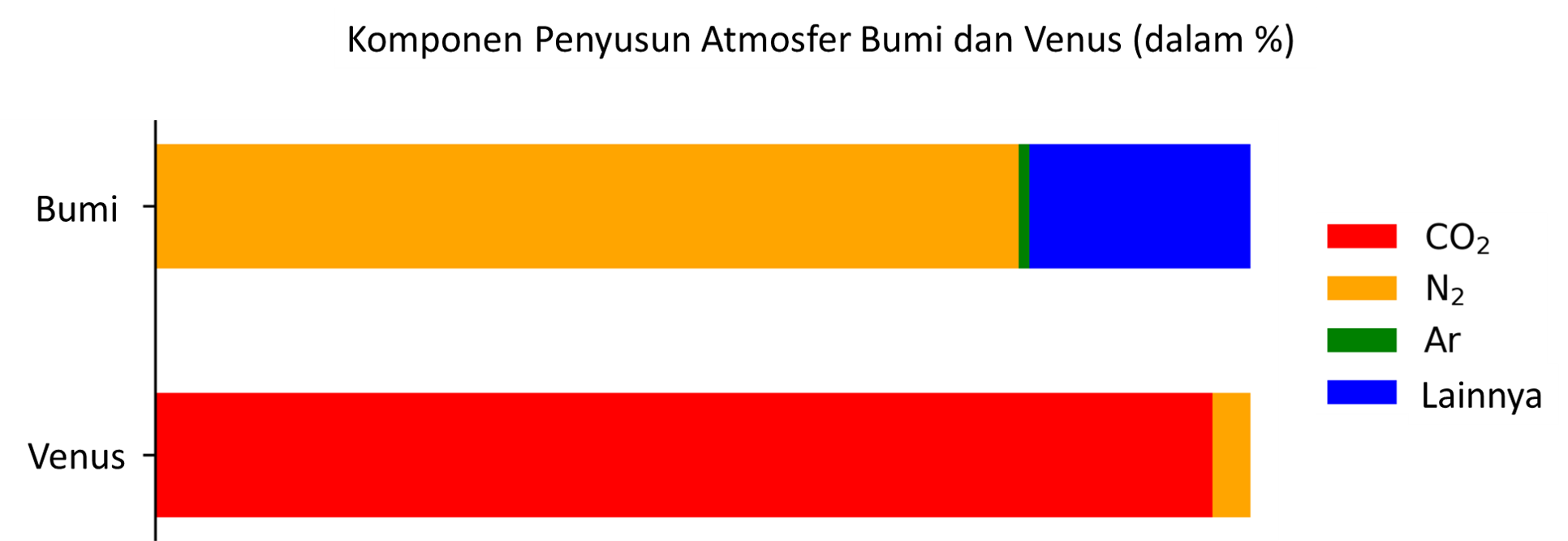
Berdasarkan data tersebut, kemungkinan efek rumah kaca terjadi lebih besar di ... dan planet yang memiliki suhu permukaan rata-rata yang lebih rendah adalah ....
Fisika
Level 11
Fisika
Pemanasan Global
Pemanasan Global dan Efek Rumah Kaca
Kelas XI
Kurikulum 2013
K13
Cek Contoh Kuis Online
Kejar Kuis
Cek Contoh Bank Soal
Kejar Soal
Kelompok lipid yang terlibat dalam penyusun lapisan kutikula pada permukaan daun tanaman adalah ....
Jika titik ditranslasikan oleh 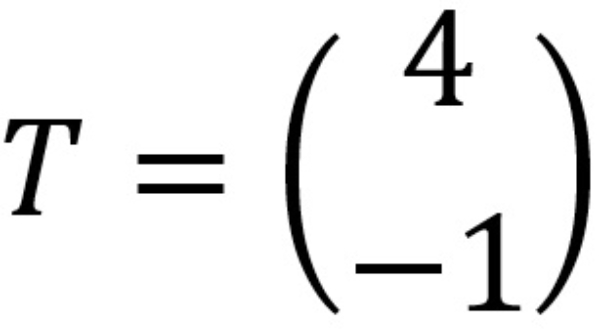
Complete the dialogue below.

Renny: I’ve been working since 8 in the morning. Now, I feel tired and hungry.
Dan: ______
Perhatikan beberapa pernyataan terkait notasi sigma berikut!
Pernyataan yang benar ditunjukkan oleh nomor ....
Berikut ini yang bukan merupakan benda yang mengandung senyawa hidrokarbon adalah ....
Perhatikan gambar berikut.
Titik berat bangun tersebut adalah ....
Membran sel bersifat impermeabel terhadap molekul di bawah ini, kecuali ....
Berdasarkan aturan Markovnikoff, reaksi adisi terhadap 4-metil-2-pentena dengan asam klorida menghasilkan suatu senyawa berupa ....
Himpunan penyelesaian untuk persamaan trigonometri pada interval adalah ....
Perhatikan data komponen penyusun atmosfer dua planet di tata surya berikut!
Berdasarkan data tersebut, kemungkinan efek rumah kaca terjadi lebih besar di ... dan planet yang memiliki suhu permukaan rata-rata yang lebih rendah adalah ....



